Третий признак равенства треугольников

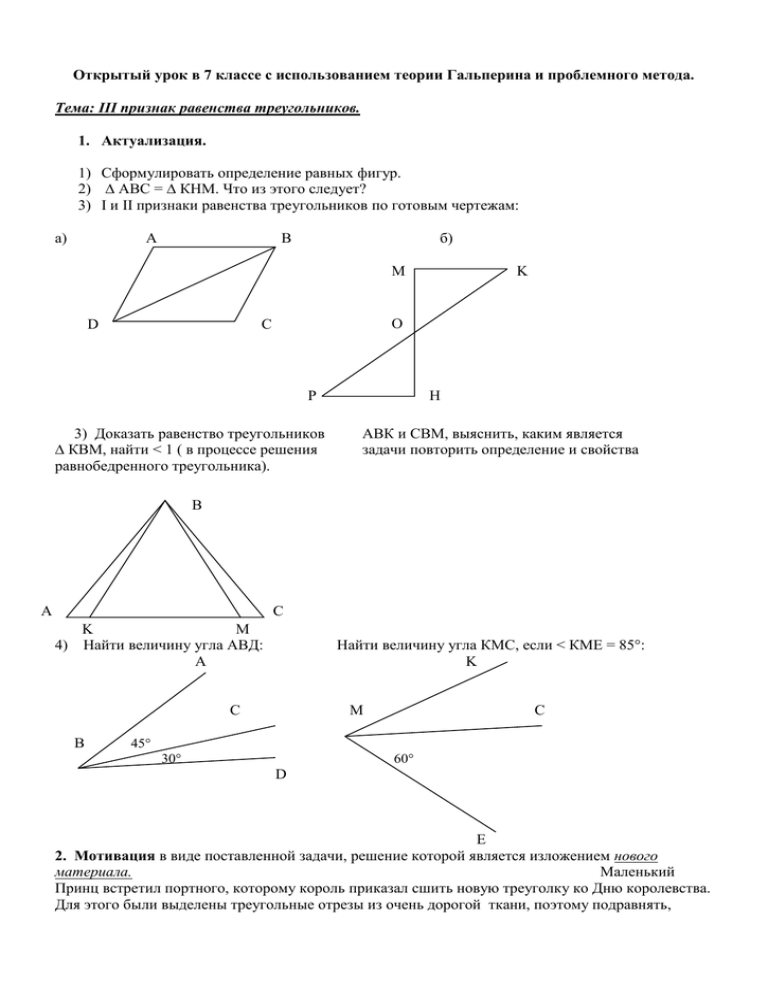
Открытый урок в 7 классе с использованием теории Гальперина и проблемного метода.
Тема: III признак равенства треугольников.
1. Актуализация.
1) Сформулировать определение равных фигур.
2) ∆ АВС = ∆ КНМ. Что из этого следует?
3) I и II признаки равенства треугольников по готовым чертежам:
а)
А
В
б)
M
С
D
K
O
P
3) Доказать равенство треугольников
∆ КВМ, найти < 1 ( в процессе решения
равнобедренного треугольника).
H
АВК и СВМ, выяснить, каким является
задачи повторить определение и свойства
B
С
A
K
M
4) Найти величину угла АВД:
A
Найти величину угла КМС, если < КМЕ = 85°:
K
C
B
M
C
45°
30°
60°
D
Е
2. Мотивация в виде поставленной задачи, решение которой является изложением нового
материала.
Маленький
Принц встретил портного, которому король приказал сшить новую треуголку ко Дню королевства.
Для этого были выделены треугольные отрезы из очень дорогой ткани, поэтому подравнять,
подрезать ничего нельзя. И наложить отрезы друг на друга точно портной не может, так как на
ткани довольно крупные драгоценные камни, которые не позволяют это сделать, да и ткань не
хочет ни на чём, кроме голого стола, даже без скатерти, лежать ровно. Но если портной сошьёт не
те кусочки, ошибётся даже на миллиметр, не сносить ему головы. Маленький принц посоветовал
портному измерить края всех отрезов. Те, у которых все края окажутся соответственно равными,
будут от одной треуголки. Давайте проверим, действительно ли прав Маленький Принц. Пусть
треугольники АВС и А1В1С1 изображают драгоценные отрезы. Расположим их таким образом,
чтобы равные стороны АС и А1С1 наложились друг на друга и совпали. По условию АВ = А1В1, ВС
= В1С1. Какими будут являться треугольникиАВВ1 и СВВ1? (Чертеж достраивается в процессе
беседы).
В
Дано: ∆ АВС и ∆ А1В1С1,
113
АВ = А1В1, ВС = В1С1, АС = А1С1
Доказать: ∆ АВС = ∆ А1В1С1
1
3
Доказательство:
1) Совместим АС и А1С1
2) Доп.построение: ВВ1
3) ∆ АВВ1 равнобедренный => <1 = < 2
А
С (С1 )
}=><В = <В1
4) ∆ СВВ1 равнобедренный => <3 = < 4
5) 1. АВ = А1В1
(А1)
2. ВС = В1С1 } => ∆ АВС = ∆ А1В1С1по двум
2
4
3. <В = <В1
сторонам и углу между ними
▄
В1
Маленький Принц помог портному спасти свою голову, а какой вывод можем сделать
мы, решив эту задачу?
(Формулировка III признака равенства треугольников).
Итак, мы получили ещё один признак равенства треугольников.
Ребята, но отрезы могли быть такими треугольниками, что при совмещении одной пары
равных сторон, получались бы такие ситуации:
В
В
С (С1)
А(А1)
С(С1 )
А
(А1)
В1
В1
Дома к следующему уроку докажите равенство треугольников АВС и А1В1С1 для этих случаев
самостоятельно.
Итак, для того, чтобы доказать равенство треугольников, используя III признак равенства
треугольников, необходимо выполнить следующие шаги: (ориентировочная карта крепится на
доску).
1. Найди и запиши первую пару равных сторон.
2. Найди и запиши вторую пару равных сторон.
3. Найди и запиши третью пару равных сторон или общую сторону.
4. Сделай вывод.
3. Закрепление.
I. Пошагово фронтально (чертёж на доске, «раскладушка»)
В
А
Доказать: ∆ ВДА = ∆ ВДС
Д
С
II. По вариантам с проговариванием (устно по очереди)
В
N
А
C
R
А
F
D
После обсуждения заслушать по одному человеку от каждого варианта.
III. Самостоятельно (2 ученика на скрытых досках)
В
А
Дано:
АВ = СД, ВД = АС
< А = 45°
Найти: < Д
С
Д
4. Итог урока :
Какие треугольники являются равными?
По каким признакам мы можем определить, что треугольники равны?
Сформулируйте еще раз признак равенства треугольников, изученный сегодня на уроке
Устно по готовому чертежу:
В
А
ВК – медиана равнобедренного треугольника АВС.
Всеми способами (по очереди) доказать, что
∆ АВК = ∆СВК
К
С
Д / З: п.20 (доказать теорему для 2 случаев самостоятельно), № 140