Практическая работа.
реклама
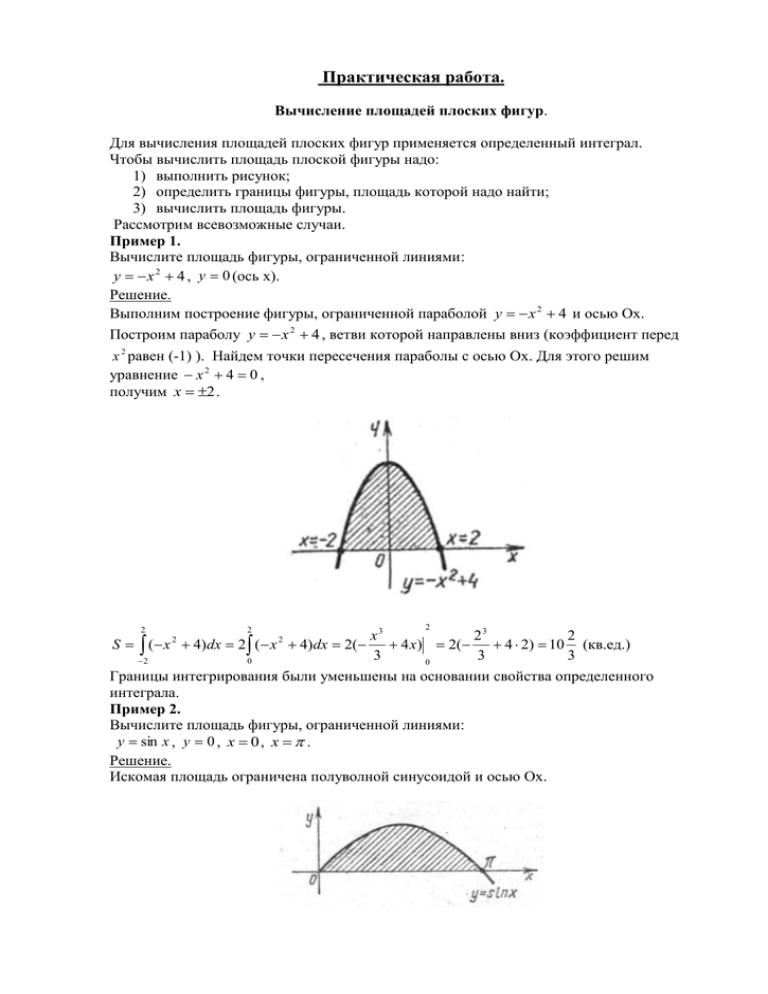
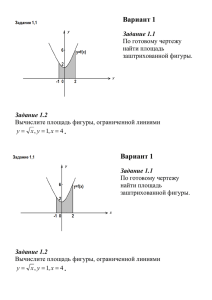
Практическая работа. Вычисление площадей плоских фигур. Для вычисления площадей плоских фигур применяется определенный интеграл. Чтобы вычислить площадь плоской фигуры надо: 1) выполнить рисунок; 2) определить границы фигуры, площадь которой надо найти; 3) вычислить площадь фигуры. Рассмотрим всевозможные случаи. Пример 1. Вычислите площадь фигуры, ограниченной линиями: у х 2 4 , у 0 (ось х). Решение. Выполним построение фигуры, ограниченной параболой у х 2 4 и осью Ох. Построим параболу у х 2 4 , ветви которой направлены вниз (коэффициент перед х 2 равен (-1) ). Найдем точки пересечения параболы с осью Ох. Для этого решим уравнение х 2 4 0 , получим х 2 . 2 2 2 x3 23 2 S ( x 4)dx 2 ( x 4)dx 2( 4 x) 2( 4 2) 10 (кв.ед.) 3 3 3 2 0 0 Границы интегрирования были уменьшены на основании свойства определенного интеграла. Пример 2. Вычислите площадь фигуры, ограниченной линиями: у sin x , y 0 , x 0 , x . Решение. Искомая площадь ограничена полуволной синусоидой и осью Ох. 2 2 S sin xdx cos x 0 cos cos 0 1 1 2 (кв.ед.) 0 Пример 3. Вычислите площадь фигуры, ограниченной линиями: у 6 х , у 0 , х 4 . Решение. Построим прямые у 6 х и х=4. Фигура, ограниченная указанными линиями, располагается ниже оси Ох. 4 4 6x 2 S 6 xdx 6 xdx 2 0 0 4 3 4 2 48 (кв.ед.) 0 Пример 4. Вычислите площадь фигуры, ограниченной линиями: х 2у 4 0 , х у 5 0 и у 0 . Решение. Выполним построение фигуры. Запишем функции в привычном виде у 0,5 х 2 и у 5 х . Для них составим таблицы : для первой х -4 0 у 0 2 для второй х 5 0 у 0 5 Найдем точку пересечения прямых, для этого составим и решим систему уравнений у 0,5 х 2, у 5 х Получим х=2, у=3. На рисунке это точка М(2;3). Искомая площадь фигуры состоит из суммы площадей двух треугольников АМN и СМN. Вычислим площадь каждого из них и сложим полученные результаты. 2 0,5 x 2 (0,5 x 2)dx 2 x (0,25 2 2 2 2) (0,25 (4) 2 2 (4)) 1 4 (4 8) 9 2 4 4 2 S ΔAMN 5 x2 52 22 25 S ΔCMN ( x 5)dx 5 x 5 5 5 2 25 2 10 4,5 . 2 2 2 2 2 2 Площадь всей фигуры будет: S 9 4,5 13,5 (кв.ед.) Пример 5. Вычислите площадь фигуры, ограниченной линиями: у х2 , у 2х . Решение. Данная фигура ограничена параболой у х 2 и прямой у 2 х . 5 Найдем точки пересечения прямых, для этого составим и решим систему уравнений у х2 , у 2х Получим х=0, х=2. 2 2x 2 x 3 23 8 1 S (2 x x )dx (2 2 ) 4 1 (кв.ед) 3 0 3 3 3 2 0 2 2 Задачи для самостоятельного решения. Вычислите площади фигур, ограниченных указанными линиями: 1вариант. 1. у 7 х , х=3, х=5, у=0. 8 2. у , х= - 8, х= - 4, у=0. х 3. у 0,5 х 2 4 х 10 , у х 2 . 4. у х 2 , у х 6 , х=-6 и координатными осями. 2 вариант. 1. у 4 х 2 , у=0. 2. у cos х , х , х , у=0. 2 3. у х 2 8 х 18 , у 2 х 18 . 1 4. у х , у , х=4. х 3вариант. 1. у х 2 6 х , х= -1, х=3,у=0. 2. у=-3х, х=1, х=2,у=0. 3. у х 2 10 х 16 , у=х+2. 4. у 3 х , у=-х+4 и координатными осями. 4вариант. , х , у=0. 3 2. у х 2 4 , х=-1, х=2, у=0. 3. у х 2 2 х 3 , у 3 х 1 . 1. у sin x , х 4. у х 2 , у х 4 , у=0. 2