арь ж ь ср Ґ п ып арь ж п f (a, b) ∈ I a b ∫ b af(t) dt = [F(t
реклама

Cours
Intégration
1- Calul Intégral
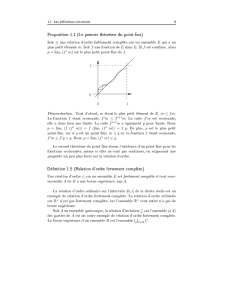
Dénition : Soit f dénie et ontinue sur
I , intervalle de R , (a, b) ∈ I 2 , on appelle intégrale de a à b de f le réel
Z
b
a
b
f (t) dt = F (t) a = F (b) − F (a).
Théorème : Intégration par parties : Si uZ et v sont deux fontions de lasse
C 1 sur un intervalle I alors
Z
b
h
ib
u′ (t)v(t) dt = u(t)v(t) −
∀(a, b) ∈ I 2 ,
a
a
b
u(t)v ′ (t) dt
a
Théorème : Changement de variable : Soit ϕ ∈ C 1 (I), I intervalle, (α, β) ∈ I 2 , f ontinue sur J , intervalle,
J ⊂ ϕ(I),
alors
Z
β
f (ϕ(t))ϕ′ (t) dt =
α
Linéarité
: (λ, µ) ∈ R 2 ,
Relation de Chasles
:
Z
b
a
b
ϕ(β)
f (u) du
ϕ(α)
f , g , fontions intégrables sur I , intervalle de R ontenant a, b, c.
Z b
Z b
(λf (t) + µg(t)) dt = λ
f (t) dt + µ
g(t) dt.
2- Propriétés des intégrales
Z
Z
a
f (t) dt +
a
Croissane de l'intégration
Z
c
f (t) dt =
b
: seulement si a<b
Z
a
c
f (t) dt.
a
si f est une fontion ontinue et f > 0 sur [a, b], alors
Z
b
de plus
f (t) dt > 0
a
Si f 6 g sur [a, b] alors
b
Z
f (t) dt 6
a
égalité de la moyenne
Le réel
1
b−a
Z
b
Z
b
Z
b
f (t) dt = 0 ⇔ ∀x ∈ [a, b], f (x) = 0
a
g(t) dt
a
: Si f une fontion ontinue sur [a, b], ∃c ∈ [a, b],
1
b−a
Z
b
f (t) dt = f (c).
a
f (t) dt s'appelle valeur moyenne de la fontion f sur le segment [a, b].
a
Sommes de Riemann
: Si f une fontion ontinue sur [a, b], alors
Z 1
n
1X
k
lim
f
=
f (t) dt.
n→+∞ n
n
0
k=0
3- Extensions
Z
b
Z
b
Dénition : Si f est prolongeable par ontinuité sur [a, b], f˜, son prolongement alors
f (t) dt =
f˜(t) dt.
a
a
Dénition : On dit que f est ontinue par moreaux sur [a, b] si il existe un nombre ni de points (xi )i∈[[0,n]] ,
def
a = x0 < x1 < x2 < · · · < xn = b, tels que les restritions de f à ]xi , xi+1 [ soient prolongeables par ontinuité sur
[xi , xi+1 ].
Z b
n−1 Z xi+1
def X
Dénition : Si f est ontinue par moreaux sur [a, b],
f (t) dt
f (t) dt =
(Chasles).
a
HMéthode Résolution (E) : y
′
i=0
xi
+ a(x)y = b(x)
où a et b sont des fontions ontinues
Les solutions de (H) : y ′ + a(x)y = 0 (équation homogène assoiée) sur I sont les fontions de la forme
yH = Ce−A(x) où A est une primitive de a et C ∈ R .
On herhe ensuite une solution partiulière y0 de (E) sous la forme y0 (x) = C(x)e−A(x) .
HMéthode Résolution de (E) : ay” + by′ + cy = f (x)
où a, b, c sont des réels et f une fontion ontinue sur I , intervalle de R .
(H) : ay ′′ + by ′ + cy = 0, l'équation homogène assoiée,
(Ec ) : ar2 + br + c = 0, l'équation aratéristique assoiée à (H).
Solutions de Ec
(r1 , r2 ) ∈ R 2 , r1 6= r2
r0 ∈ R
r = α ± βi ∈ C
Solutions de (H) f : x 7→ λ1 er1 x + λ2 er2 x f : x 7→ (λx + µ)er0 x f : x 7→ eαx (A cos βx + B sin βx), (A, B) ∈ R 2
Lorsque f est de la forme t 7→ P (t)emt alors on herhe une solution partiulière du type t 7→ Q(t)emt , Q étant
un polynme dont on indiquera le degré.
Lorsque f est de la forme t 7→ sin(ωt) ou t 7→ cos(ωt), il existe une solution partiulière du type
t 7→ A sin(ωt) + B cos(ωt) si iω n'est pas solution de (Ec ),
t 7→ t(A sin(ωt) + B cos(ωt)) si iω est solution de (Ec ),
A et B étant à déterminer.
Théorème : L'ensemble des solutions de (E) est SE = {y0 +yH , yH solution de (H)} dans les deux types d'équation.
BCPST1A - Poinaré
!