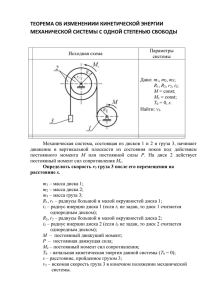
МИНОБРНАУКИ РОССИИ фе де ра л ь но е го су да рс т венно е б ю д жет но е о б ра зо ва т ел ьно е у ч ре жд ение высш его о б ра зо ва ния «Балтийский государственный технический университет «ВОЕНМЕХ» им. Д.Ф. Устинова» (БГТУ «ВОЕНМЕХ» им. Д.Ф. Устинова) ОТЧЕТ по курсовой работе Тема Исследование механической системы Редуктор 10.3 – Груз 2.3 Обучающегося группы Е421С Топориков Д.А. группа Фамилия и инициалы Направление подготовки / специальность 17.05.01 Боеприпасы и взрыватели индекс полное наименование направления подготовки / специальности Направленность образовательной программы Патроны и гильзы профиль / специализация / магистерская программа Дисциплина (модуль) Теоретическая механика Руководитель: Ст. преподаватель ученая степень, ученое звание Оценка: « » Обучающийся: подпись Чирков В.Ю. Фамилия ИО 20 24 г. Топориков Д.А. подпись Фамилия ИО « » САНКТ-ПЕТЕРБУРГ 2024 г 20 24 г. Реферат В рамках курсовой работы были исследованы механические системы с редукторами, которые являются одним из наиболее распространенных компонентов в различных машинах и устройствах. Редукторы - это устройства, которые применяются для снижения скорости вращения двигателя и увеличения крутящего момента. Они находят широкое применение в промышленности, транспорте, сельском хозяйстве и других отраслях. Курсовая работа была направлена на исследование кинематики и динамики механической системы с редуктором. Она включала анализ преобразования кинетической энергии между элементами системы, а также изучение влияния различных параметров на динамику работы редуктора. В ходе работы были выполнены кинетический расчет редуктора, расчет кинетической энергии системы, вычисление элементарной работы сил, определено натяжение свободного участка троса, определение силы реакции наклонной плоскости и коэффициента трения, определение силы взаимодействия между двумя шестернями редуктора. Таким образом, данная курсовая работа представляла собой комплексное исследование работы механической системы с редуктором, охватывающее разнообразные аспекты функционирования данной системы. Объём работы составлял 17 страниц и включал 7 рисунков, а также 4 источника информации. 2 Содержание Введение ................................................................................................................... 4 1. Кинематический расчёт редуктора .................................................................... 6 2. Расчёт кинетической энергии системы ............................................................. 7 4. Натяжение свободного участка троса ............................................................. 12 5. Определение силы реакции наклонной плоскости и коэффициента трения скольжения груза ................................................................................................... 13 6. Силы взаимодействия между двумя шестернями редуктора ........................ 15 Заключение............................................................................................................. 16 Список использованных источников .................................................................. 17 3 Введение Для подъема и перемещения груза применяют механизм, называемый грузовой лебедкой, которая состоит из двигателя, ведущего вала 1, планетарного редуктора, ведомого вала 2, барабана и троса (см. рис. 1). Двигатель, редуктор и барабан лежат на одной оси, поднимаемый груз Q находится на наклонной плоскости с углом наклона α. [1] Лебедка приводится в движение двигателем. Ведущему валу двигателя сообщается постоянный вращательный момент M1=1,2M0 (момент 𝑀0 удерживает систему в покое, и его величину рассчитывают в процессе решения задачи). Планетарный редуктор предназначен для передачи крутящего момента от двигателя непосредственно к приводу. Редуктор состоит из набора взаимно зацепленных зубчатых колес с перемещающимися осями, которые, в свою очередь, способны вращаться вокруг неподвижных осей. Одно из колес в редукторе установлено неподвижно. Так как подвижные шестерни движутся вокруг одного центра, то вся конструкция напоминает солнечную систему, и поэтому редуктор называется планетарным, а подвижные шестерни – сателлитами. [2] Груз Q поднимается по наклонной плоскости без скольжения, коэффициент трения качения 𝑓тр.к.. Силы сопротивления, приложенные к механизму редуктора условно приводятся к моменту М2, приложенному к ведомому валу, величина которого принимается пропорциональной угловой скорости вала: M2 = k𝜔2. [1] Выполнение данной курсовой работы позволит расширить понимание в области теоретической механики, развить навыки математического моделирования и анализа механических систем, а также получить опыт в решении реальных инженерных задач. Определить: 4 1) используя теорему об изменении кинетической энергии для механической системы: [1] а) дифференциальное уравнение движения ведущего вала 1; б) закон изменения угловой скорости вала 1, движущегося из состояния покоя до установившегося движения. Привести график этой зависимости; в) угловую скорость установившегося движения; 2) используя теорему об изменении кинетического момента системы: г) силы взаимодействия между двумя сцепленными шестернями (по выбору); д) закон изменения натяжения троса в зависимости от времени и его установившееся значение; 3) из уравнения движения груза по наклонной плоскости ж) силу реакции наклонной плоскости и) коэффициент трения скольжения, обеспечивающий качение груза по наклонной плоскости без скольжения Дано: I4-6, m4-6, mгр, ρ, R3, R4, R6, I1-3, м м м кг*м2 кг*м2 кг*м2 кг 0,1 0,04 0,03 1 0,5 I2-7, 3 1 fтр.к, R, кг м м 8 0,6 0,03 0,7 r, м 𝛼° м 0,5 20 В данной работе рассматривается редуктор, представленный на (рис.1) Рис. 1 Рис. 2 В процессе работы был также рассмотрен груз, представленный на рисунке 2. 5 1. Кинематический расчёт редуктора В редукторе (рис.3) ведущий вал 1 вращается с угловой скоростью ω1. Шестерня 3, вращаясь с угловой скоростью ω1 приводит в движение систему шестерней 4 и 6, закреплённых на общей оси 4-6. Шестерня 4 находится в зацеплении с неподвижной (опорной) шестерней 5 корпуса редуктора. Водило 7, зацепленное на оси 4-6, приводит в движение ведомый вал 2. Рис.3 Для расчета кинематики редуктора воспользуемся методом мгновенного центра скоростей. Точка К является мгновенным центром скоростей. R 3 ∙ ω1 = ωr (R 6 + R 4 ) R3 ω R4 + R6 1 R3 ωa = ωr + ω1 = (1 + )ω R4 + R6 1 ωr = ωr R 4 = ω2 (R 3 − R 6 ) Таким образом, ω 2 = ωr R4 R3 R4 = ω R 3 − R 6 (R 4 + R 6 ) (R 3 − R 6 ) 1 (1.1) Передаточное число редуктора: i= ω2 R3R4 0,1 ∙ 0,04 = = = 0,8 ω1 (R 4 + R 6 )(R 3 − R 6 ) (0,04 + 0,03)(0,1 − 0,03) 6 2. Расчёт кинетической энергии системы Кинетическая энергия редуктора. 𝑇 = 𝑇1−3 +2·𝑇4−6 + 𝑇2−7 Шестерня 3 и вал 1 вращаются вокруг неподвижной оси и их кинетическая энергия. 1 T1−3 = I1−3 ω12 2 Шестерни 4-6 совершают сложное движение. Момент инерции относительно мгновенной оси вращения определяется с помощью теоремы Штейнера: IK = I4−6 + m4−6 R24 В итоге, 1 1 R3 T4−6 = (I4−6 + m4−6 R24 )𝜔𝑎2 = (I4−6 + m4−6 R24 )ω12 (1 + )2 2 2 R4 + R6 Шестерня 7 с ведомым валом и барабаном вращается вокруг неподвижной оси и их кинетическая энергия равна: 1 1 R3 R4 1 T2−7 = I2−7 ω22 = I2−7 ( ω1 )2 = I2−7 ω12 𝑖 2 (R 4 + R 6 ) (R 3 − R 6 ) 2 2 2 Суммарная кинетическая энергия лебёдки: Tлеб = 1 2 𝑅3 ∙ ω1 ∙ (I1−3 + 2(I4−6 + m4−6 ∙ R24 )(1 + )2 + I2−7 𝑖 2 ) 2 𝑅4 + 𝑅6 Кинетическая энергия груза определяется по теореме Кенига (рис. 4) 1 1 2 Тгр = mгр vгр + Iгр ω2гр 2 2 где ωгр = ω2 rбар ω1 𝑖rбар = R+r R+r ω1 𝑖rбар R vгр = ωгр R = R+r 7 (2.1) 𝐼гр = 1 ∙ 𝑚гр ∙ 𝜌2 2 𝑟бар − радиус барабана Рис.4. Барабан и поднимаемый груз (вид сбоку) Кинетическая энергия системы равна сумме кинетических энергий лебедки и груза (2.2): [4] 1 𝑇 = 𝑇леб + 𝑇гр = ∙ 𝜔12 ∙ 𝐼пр 2 Т= 1 2 𝑅3 ∙ ω1 ∙ (I1−3 + 2(I4−6 + m4−6 ∙ R24 )(1 + )2 + I2−7 𝑖 2 ) 2 𝑅4 + 𝑅6 (2.2) 𝑖rбар R 2 𝑖rбар 2 1 + mгр ( ) + Iгр ( ) = Iпр ω12 R+r R+r 2 Iпр = (I1−3 + 2(I4−6 + m4−6 ∙ R24 )(1 + 𝑖rбар R 2 𝑖rбар 2 + mгр ( ) + Iгр ( ) ) R+r R+r 𝑅3 )2 + I2−7 𝑖 2 𝑅4 + 𝑅6 где Iпр – приведённый момент инерции Iпр= 4,47 кг∙м2 8 3. Вычисление элементарной работы сил, действующих на систему Работа сил на элементарном перемещении при движении груза без проскальзывания (рис. 5) Рис.5. Плоское движение груза Таким образом, ∆A = M1𝑑𝜑1 − M2d𝜑2 − Pгрdh − Mтр.к.d𝜑гр Отметим, что только работа момента М1 входит с положительным знаком в работу ∆А, так как моменты М2 , Мтр.к. и сила Ргр имеют отрицательную мощность. [1] Из соотношений (1.1) и (2.1) d𝜑2 = z2d𝜑1, d𝜑гр = zгрd𝜑1, dh = z𝑐 sin 𝛼 d𝜑1, где z2 = 𝑖 = 0,8 , zгр = 𝑖rбар R+r = 0,048 , zc = 𝑖rбар R R+r = 0,033 и, следовательно, ∆A = M1 dφ1 − M2 z2 dφ1 − Pгр zc sin α dφ1 − Mтр.к zгр dφ1 (3.1) Момент М2 по условию пропорционален угловой скорости 𝜔 2: M2 = kω2 = 𝑘𝑧2 𝜔1; M2 = 1,072𝜔1 Момент трения качения Мтр.к. определяется по закону Mтр.к. = fтр.к.N , 9 где N – нормальная составляющая реакции наклонной плоскости на груз. Для ее нахождения требуется рассмотреть уравнения плоскопараллельного движения груза: mгр𝑥̈ c = S + Fтрx − mгрg∙sin 𝛼 (3.2) mгр𝑦̈ c = N − mгрg∙cos 𝛼 (3.3) Iгр𝜑̈ гр = −SR + FтрX + fтр.к.N (3.4) Так как yc=const, то и, следовательно, из уравнения (3.3) следует, что: N = mгрgcos 𝛼 Для нахождения зависимости ω1 (t) воспользуемся теоремой об изменении кинетической энергии. Сила S является внутренней силой системы и при не растяжимости троса ее работа равна нулю. [1] Дифференциал кинетической энергии в соответствии с выражением (2.2) имеет вид: dT = Iпр𝜔1ω̇ dt = Iпрω̇d𝜑1 (3.5) Формула (3.1) для элементарной работы переписывается следующим образом: ∆A = (M1 – k𝑧2 𝜔1 − Pгрz𝑐 sin 𝛼 − Mтр.к.zгр)d𝜑1 (3.6) При равновесии ω1=0 и ∆А = 0. При этом вместо момента М1 к первому валу прикладывается момент М0, который удерживает систему в равновесии. Следовательно, M0 = Pгрzc∙sin 𝛼 + Mтр.к.zгр = 0,89 Н ∙ м Далее по условию задачи M1 = 1.2M0 = 1,07 Н ∙ м Подставим выражения (3.5) и (3.6) в теорему об изменении кинетической энергии dT=∆A и сократим обе части на d𝜑1. В результате этих действием записываем дифференциальное уравнение для определения угловой скорости первого вала [2] Iпр dω1 = M1 − kz2 ω1 − Pгр zc sin α − Mтр.к. zгр dt 10 которое является дифференциальным уравнением с разделяющимися переменными и имеет аналитическое решение (рис.6) ω1 (t) = G D ∙ (1 − 𝑒𝑥𝑝 − D t Iпр ) (3.7) где G = M1 − Pгр zс sin α − Mтр.к zгр G=1,07 − 78,48 ∙ 0,033 ∙ sin 20° − 2,212 ∙ 0,048 = 0,078 𝐷 = 𝑘𝑧2 = 1,072 ω1 (t) = 0,072(1 − exp−0,24t ) lim ω = 0,072с−1 t→∞ Рис.6 11 4. Натяжение свободного участка троса Для нахождения силы натяжения троса S применим теорему об изменении кинетического момента для груза относительно мгновенного центра скоростей – точки C' (см. рис. 5.) (Iгр + mгр R2 )𝜔̇ 1 = S(R + 𝑟) − Mтр.к − Pгр R sin α (4.1) Здесь использовали теорему Штейнера для определения момента инерции относительно оси, проходящей через точку C' перпендикулярно плоскости рисунка. Зависимость величины 𝜔гр от времени известна, так как 𝜔гр = 𝑧гр 𝜔1 , где угловая скорость 𝜔1 (𝑡) известна из формулы (3.7). Из формулы (4.1) находим величину силы S (рис. 7) [1] S= = 1 R+r 1 [Mтр.к + Ргр R sin α + (Iгр + mгр R2 )zгр 𝜔̇ 1 ] = R+𝑟 2 G [mгр gR sin α + mгр g𝑓тр.к cos α + (Iгр + mгр R )zгр I exp пр S=17,5+0,0045𝑒𝑥𝑝(−0,24t) lim S = 17,5 H t→∞ Рис.7 12 Dt Iпр − ] (4.2) 5. Определение силы реакции наклонной плоскости и коэффициента трения скольжения груза Скорость точки контакта груза с плоскостью равна нулю: [3] vc′ = 0 = vc + ω ∙ CC′ или в проекции на ось x: ẋ c + φ̇гр R = 0 откуда следует, что . Уравнения плоского движения (3.2) и (3.4) с учетом зависимости переписываем в виде mгр ẍ c = S + Fтрx − 𝑚гр 𝑔 sin α (5.1) ẍ 2 −𝑚гр 𝜌гр ∙ c = −𝑆𝑟 + Fтрx R + 𝑓тр.к mгр 𝑔 cos α R (5.2) 2 Здесь учтена зависимость 𝐼гр = 𝑚гр ∙ 𝜌гр , где 𝜌гр – радиус инерции груза относительно оси, проходящей через его центр перпендикулярно рисунку. Из (5.2) получаем: 𝑅𝑟 𝑅2 𝑅 𝜌гр 𝜌гр 𝜌гр 𝑚гр ∙ 𝑥̈ 𝑐 = 𝑆 ∙ 2 − 𝐹тр𝑥 ∙ 2 − 𝑓тр.к ∙ 𝑚гр ∙ 𝑔 ∙ 2 ∙ cos 𝛼 (5.3) Так как левые части выражений (5.1) и (5.3) одинаковы, то равными должны быть и правые части этих соотношений: 𝑅𝑟 𝑅2 𝑅 𝑆 + 𝐹тр𝑋 − 𝑚гр ∙ 𝑔 ∙ 𝑠𝑖𝑛 𝛼 = 𝑆 ∙ 2 − 𝐹тр𝑥 ∙ 2 − 𝑓тр.к ∙ 𝑚гр ∙ 𝑔 ∙ 2 ∙ cos 𝛼 𝜌гр 𝜌гр 𝜌гр откуда 𝑅2 𝑅𝑟 𝑅 𝐹тр𝑋 ∙ (1 + 2 ) = 𝑆 ∙ ( 2 − 1) + 𝑚гр ∙ 𝑔 ∙ (sin 𝛼 − 𝑓тр.к ∙ 2 ∙ cos 𝛼) 𝜌гр 𝜌гр 𝜌гр и окончательно, 2 2 𝑆(𝑅𝑟 − 𝜌гр ∙ sin 𝛼 − 𝑓тр.к ∙ 𝑅 ∙ cos 𝛼) ) + 𝑚гр ∙ 𝑔 ∙ (𝜌гр 𝐹тр𝑋 = 2 + 𝑅2 𝜌гр 17,5 ∙ (0,7 ∙ 0,5 − 0,62 ) + 8 ∙ 9,81 ∙ (0,62 ∙ sin 20° − 0,03 ∙ 0,7 ∙ cos 20° ) Fтрх = 0,62 + 0,72 13 𝐹трх = 9,34 H Определение коэффициента трения скольжения груза, обеспечивающего его подъём по наклонной плоскости без скольжения. Условие отсутствия проскальзывания груза по наклонной плоскости |𝐹тр𝑥| ≤𝑓𝑚гр𝑔𝑐𝑜𝑠𝛼 |9,34| ≤𝑓∙8∙9,81∙𝑐𝑜𝑠20° и, следовательно, 2 2 𝑆(𝑅𝑟 − 𝜌гр ∙ sin 𝛼 − 𝑓тр.к ∙ 𝑅 ∙ cos 𝛼) ) + 𝑚гр ∙ 𝑔 ∙ (𝜌гр 𝑓≥ 2 + 𝑅 2 )𝑚 𝑔 cos 𝛼 (𝜌гр гр 𝑓 ≥ 0,127 14 6. Силы взаимодействия между двумя шестернями редуктора Взаимодействие между шестеренками 6 и 7 определим с помощью теоремы об изменении кинетического момента, которую составим относительно неподвижной оси, совпадающей с валом 2. [1] Используем теорему об изменении кинетического момента относительно второго вала, с которым жестко соединена шестеренка 7 и барабан, на который наматывается трос. На шестеренку 7 со стороны шестерни 6 действует сила S6 (рис. 5). Ко второму валу приложен момент сопротивления в редукторе M2= k𝜔2= kz2𝜔1. Теорема об изменении кинетического момента позволяет записать дифференциальное уравнение. [1] I2−7 ω̇2 = S6 R 7 − M2 − Srбар откуда S6 = 1 (M + Srбар + I2−7 ω̇2 ) R7 2 G Здесь S6=S, момент М2 = kz2 (1 − 𝑒𝑥𝑝 D z2 G Iпр 𝑒𝑥𝑝 − D t Iпр D t Iпр − ) и, наконец, ω̇2 = : Dt Dt 1 G G − − Iпр Iпр S6 = exp (kz2 (1 − exp )) + I2−7 z2 R7 D Iпр rбар (mгр gR sin α + mгр gfтр.к cos α R+r Dt G − Iпр 2 + (Iгр + mгр R )zгр exp ) Iпр + S6 = 8,11 Н 15 Заключение В результате проведённой работы были получены следующие значения и зависимости для искомых величин: 1. Передаточное число редуктора i= ω2 = 0,8 ω1 2. Угловая скорость первого вала установившегося движения была определена с помощью теоремы об изменении кинетической энергии продифференцировав его ωуст = lim ω = 0,072 с−1 t→∞ 3. Натяжение свободного участка троса в зависимости от времени Sуст = lim S = 17,5 Н t→∞ 4. Сила реакции наклонной плоскости, обеспечивающего подъем груза по наклонной плоскости без проскальзывания Fтрх = 9,34 Н 5. Коэффициент трения скольжения груза |f| ≥ 0,127 6. Взаимодействие между двумя шестернями редуктора определили с помощью теоремы об изменении кинетического момента, которую составили относительно неподвижной оси S6 = 8,11 H 16 Список использованных источников 1) Динамика: пособие по выполнению расчётно-графических работ / Г.Т. Алдошин [и др.]; под ред. Г.Т. Алдошина; Балт. гос. техн. ун-т. – СПб., 2016. 2) Бутенин, Н.В. Курс теоретической механики. Т.2 / Н.В. Бутенин , Я.Л. Лунц, В.Р. Меркин. СПб.: Лань. 2002. 3) Курс теоретической механики / Ред. К.С. Колесников. М.: Изд-во МГТУ им. Н.Э. Баумана. 2002. 4) Бать, М.И. Теоретическая механика в примерах и задачах. Т.2. Динамика / М.И. Бать, Г.Ю. Джанелидзе, А.С. Кельзон. СПб.: Лань. 2013. 17