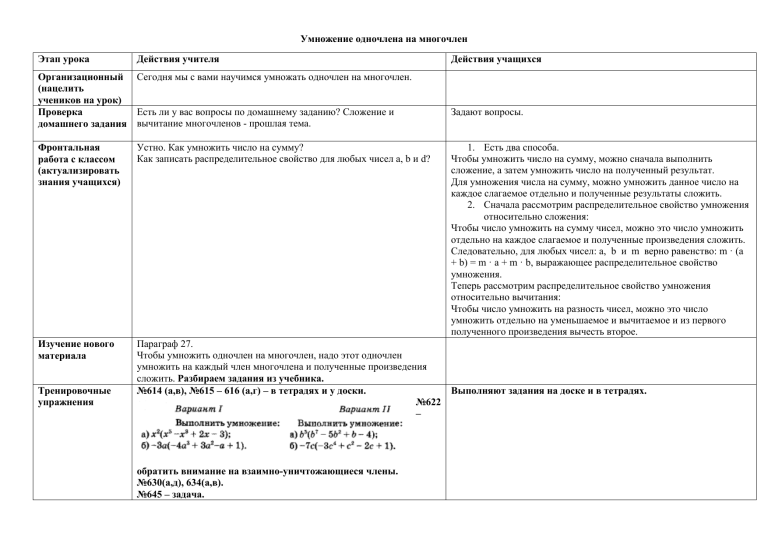
Умножение одночлена на многочлен Этап урока Действия учителя Организационный Сегодня мы с вами научимся умножать одночлен на многочлен. (нацелить учеников на урок) Есть ли у вас вопросы по домашнему заданию? Сложение и Проверка домашнего задания вычитание многочленов - прошлая тема. Действия учащихся Задают вопросы. Фронтальная работа с классом (актуализировать знания учащихся) Устно. Как умножить число на сумму? Как записать распределительное свойство для любых чисел а, b и d? Изучение нового материала Параграф 27. Чтобы умножить одночлен на многочлен, надо этот одночлен умножить на каждый член многочлена и полученные произведения сложить. Разбираем задания из учебника. №614 (а,в), №615 – 616 (а,г) – в тетрадях и у доски. Выполняют задания на доске и в тетрадях. №622 – Тренировочные упражнения обратить внимание на взаимно-уничтожающиеся члены. №630(а,д), 634(а,в). №645 – задача. 1. Есть два способа. Чтобы умножить число на сумму, можно сначала выполнить сложение, а затем умножить число на полученный результат. Для умножения числа на сумму, можно умножить данное число на каждое слагаемое отдельно и полученные результаты сложить. 2. Сначала рассмотрим распределительное свойство умножения относительно сложения: Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить. Следовательно, для любых чисел: a, b и m верно равенство: m · (a + b) = m · a + m · b, выражающее распределительное свойство умножения. Теперь рассмотрим распределительное свойство умножения относительно вычитания: Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе. Самостоятельная работа Подведение итогов Сегодня мы с вами сформулировали правило умножения одночлена на многочлен. урока Параграф 27 (до примера 3); №617, 630 , 646. Сообщение домашнего задания Выполняют задание в тетрадях.











