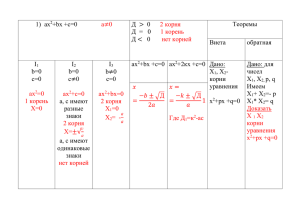
Пример решения полного квадратного уравнения, где D
реклама

1. Петрушенко Сергей Юрьевич, г. Старый Оскол, МБОУ «ООШ №17», учитель математики, высшая квалификационная категория. 2. Петрушенко Ирина Витальевна, г. Старый Оскол, МБОУ «Гимназия № 18», учитель математики, высшая квалификационная категория. Квадратным уравнением называют уравнение вида ax2+bx+c=0, где x - неизвестное, а, b, c – действительные числа, причем a ≠ 0 ax2+bx+c=0 ax2+bx=0 ax2+c=0 D>0 D=0 D<0 вычислить корень уравнения записать ответ: «корней нет» x1, 2 b –четное ax2+bx+c=0 2 b D1 a c 2 x1, 2 b D1 2 a Пример b D 2a Пример b –четное, a=1 x2+bx+c=0 2 b D1 c 2 x1, 2 b D2 2 Пример ax2+bx=0 ax2- c=0 Пример решения полного квадратного уравнения 7 1 x1, 2 8 x1 1 x2 0,75 Пример решения полного квадратного уравнения, если b - четное 2 14 D1 - 9 5 4 2 x1, 2 5 x1 9 14 4 2 9 x2 1 Пример решения полного квадратного уравнения, где b – четное, а=1 2 2 D 2 - 80 81, 2 x1, 2 2 81 2 x1 10 x2 8 При D=0 уравнение ax2+bx+c=0 имеет один корень: b x 2a Пример Пример решения полного квадратного уравнения при D = 0 4x2+12x+9=0 D= 122-4∙4∙9=0; x=-1,5 При D < 0 уравнение ax2+bx+c=0 не имеет корней Пример Пример решения полного квадратного уравнения, где D < 0 7x2-25x+23=0 D= (-25)2-4∙7∙23=625-644=-19, D<0, корней нет. Решение уравнения ax2+bx=0 в общем виде: x(ax+b)=0 x=0 или ax+b=0 x=0 или x=-b/a Пример Пример решения неполного квадратного уравнения при с=0 4x2+9x=0 x( 4x+9)=0 x=0 или 4x+9=0 x=0 или x=-2,25 Решение уравнения ax2-c=0 в общем виде: c x 0 a 2 c 0 a корней нет Пример c 0 a c c x x 0 a a x1, 2 c a Пример Пример решения неполного квадратного уравнения при b=0 c 0 a -3x2+75=0; -3(x2-25)=0; -3(x-5)(x+5)=0; x=-5 или x=5. Задание Пример решения неполного квадратного уравнения при b=0 c 0 a 3x2+6=0; 3x2=-6; x2=-2; корней нет. Из данных уравнений выбрать полные квадратные уравнения с D>0 5x 2 8x 3 0 x 2 3 10 x2 9 0 35 x 2 2 x 1 0 3x 2 3x 1 0 x 2 2 x 80 0 12 x 2 7 x 1 0 2 x 2 8 x 25 0 x 2 16 1.Н.Б.Мельникова, Г.А.Захарова. Таблицы по алгебре для общеобразовательной школы. Алгебра.Уравнения. (методические рекомендации) 2.Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова. Алгебра. Учебник для 8 класса общеобразовательных учреждений 3.Н.Я.Виленкин, А.Н. Виленкин, Г.С. Сурвило. Алгебра. Учебник для 8 класса с углубленным изучением математики