"Квадратные уравнения" 8 кл

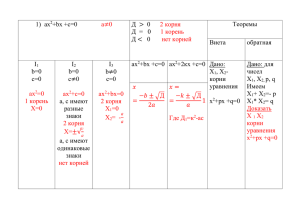
Квадратные
уравнения
Обобщение и
систематизация
знаний 8 кл.
Учитель: Штыхина Л. С.
Цели урока:




систематизировать знания учащихся по данной теме,
закрепить умение применять их, выявить проблемы и
затруднения, определить степень усвоения
материала;
формирование ответственности, организованности,
дисциплинированности учащихся;
воспитание активности, внимания,
самостоятельности;
формирование умений применения компьютера при
решении квадратных уравнений.
Определение квадратного
уравнения
Квадратный уравнением
называется уравнение вида
ax2 + bх + c = 0,
где a, b, c – произвольные числа,
причём a ≠ 0.
Коэффициенты
квадратное уравнения
 число
a–
первый (старший) коэффициент;
 число b –
второй коэффициент;
 число c –
свободный член.
Примеры квадратный
уравнений
3х2 + 5х – 3 = 0;
а=3; b=5; с=-3
-2х2 – 4х + 5 = 0;
а=-2; b=-4; с=5
х2 – х + 1 = 0;
а=1; b=-1; с=1
-х2 + 2х – 10 = 0;
а=-1; b=2; с=-10
Приведённое квадратное
уравнение
Квадратное уравнение
называется приведённым,
если первый коэффициент
равен 1.
Примеры: х2 + 5х – 3 = 0;
у2 – 8у – 4 = 0.
Дискриминант квадратного
уравнения
Дискриминант квадратного уравнения
вычисляется по формуле:
D=b2 - 4 ac;
Количество корней квадратного
уравнения зависит от дискриминанта:
если D>0 – 2 корня;
если D=0 –1 корень;
если D<0 – нет корней;
Формула корней квадратного
уравнения
Неполные квадратные
уравнения
Квадратное уравнение
называется неполным,
если
хотя бы один из коэффициентов
b и c равен нулю.
Виды неполных квадратных
уравнений
 ax2
+ bх = 0,
 ax2 + c = 0,
 ax2 = 0,
c=0
b=0
b = 0, c = 0
Уравнение вида
ax2 + bх = 0,
Решается путём разложения его
левой части на множители. Оно
всегда имеет 2 корня, причём
один из корней равен нулю.
Пример
х2 – 36х = 0,
х ( х – 36 ) = 0,
х = 0 или х – 36 = 0,
х = 36.
Ответ: х1 = 0, х2 = 36.
Уравнение вида
ax2 + с = 0,
Для решения данного уравнения
нужно перейти к виду ax2 = с.
Уравнение либо не имеет
корней, либо имеет 2 корня,
которые являются
противоположными числами.
Пример
2х2 – 50 = 0,
2х2 = 50,
х2 = 25,
х1 = 5, х2 = - 5.
Ответ: х1 = 5, х2 = - 5.
Пример
3х2 + 48 = 0,
3х2 = - 48,
х2 = - 16.
корней нет
Ответ: корней нет.
Уравнение вида
ax2 = 0,
Имеет один корень, равный о.
5х2 = 0,
х2 = 0,
х = 0.
Ответ: х = 0.
Теорема Виета
x2 + pх + g = 0,
х1 + х2 = - p;
х1 . х2 = g.
Квадратный трёхчлен
ax2 + bх + c
если х1 и х2 - корни квадратного
трёхчлена, то
ax2 + bх + c = a (х – х1)(х – х2);
если квадратный трёхчлен не имеет
корней, то
его нельзя разложить на множители.
Примеры
х2 – х – 2; х1 = 2, х2 = -1;
х2 – х – 2= (х – 2)(х+1);
100х2 +20х + 1; х = -0,1
100х2 +20х + 1=100(х +0,1)2
3х2 – 2х – 1 = 0; х1 = 1, х2 = -1/3,
3х2 – 2х – 1=3(х – 1)(х+1/3)=
=(х –1)(3х +1);