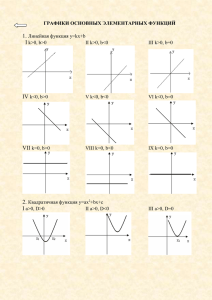
Таблица для учеников к уроку на тему "Квадратные корни
реклама
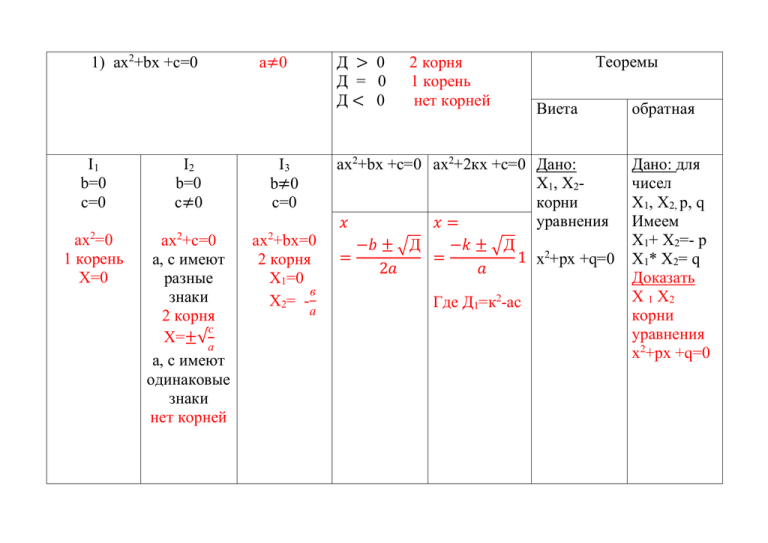
1) ax2+bx +c=0 Д > 0 Д = 0 Д< 0 a≠0 I1 b=0 c=0 I2 b=0 c≠0 I3 b≠0 c=0 ax2=0 1 корень Х=0 ax2+c=0 a, c имеют разные знаки 2 корня с Х=±√а а, с имеют одинаковые знаки нет корней ax2+bx=0 2 корня Х1=0 в Х2= а 2 корня 1 корень нет корней Теоремы Виета ax2+bx +c=0 ax2+2кx +c=0 Дано: Х1, Х2корни уравнения 𝑥 𝑥= −𝑏 ± √Д −𝑘 ± √Д = = 1 x2+рx +q=0 2𝑎 𝑎 Где Д1=к2-ас обратная Дано: для чисел Х1, Х2, p, q Имеем Х1+ Х2=- p Х1* Х2= q Доказать Х 1 Х2 корни уравнения x2+рx +q=0