242 kb - На сайт www.18ya.by.ru
реклама

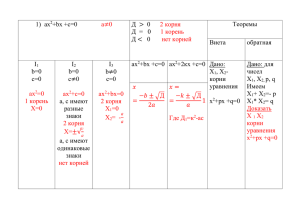
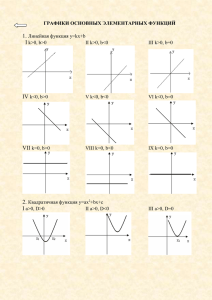
Урок с применением ЭВМ “Общие свойства функции” Учитель Цель урока. Обобщение изученных свойств функции, подготовка к исследованию некоторых рациональных функций и построению графиков. Задачи урока. Проверка знаний учащихся по теме “Функции и их свойства” с помощью компьютерного тестирования, отработка умений чтения графиков функций. Тип урока. Компьютерный урок. План урока 1. Устная работа (5 мин.) 2. Проверка д/з (№№ 112а, 113в) (5 мин.) 3. Самостоятельная работа (5-7 мин.) 4. Индивидуальные задания - 6 чел. (15-20 мин.) Компьютерные тесты - 8 чел. 4а. Работа над ошибками в самостоятельной работе. (5 мин.) 5. Устная работа (с доски). 6. №№ 114 (а, б); 116 (а, б); 117 (а, б); 119 (д). 7. Итог урока. Оценки. Выводы. 8. Домашнее задание: п.п. 24, 25; №№ 114 (в), 116(в), 117(в). Ход урока 1. (Заранее с домашним заданием - 2 чел. к доске) Устно. Работа с графиками функций (переносная доска № 1) Вопросы по графикам: - область определения; - промежутки возрастания и убывания; - четность, нечетность; - точки экстремума, экстремумы; - наибольшее (М) и наименьшее (м) значение функции; - множество значений; ограничена? - промежутки, для которых f(x)>=0, f(x)<=0. 2. Проверка домашнего задания: №№ 112а, 113в (переносная доска № 3) Вопросы по графикам: - точки экстремума; - М и м; - множество значений; - ограниченная ли? 3. Самостоятельная работа. Вариант 1 1. f(x) возрастающая. Вариант 2 1. f(x) убывающая. Сравните f(3) и f(5) 2. Начертите эскиз графика функции убывающей на [-3;0] и [3;5], возрастающей на [0;3] 3. Какие из функций y=7-8x, y=x, y=x3, y=x2, y=2x-9 являются на (-; 0) возрастающими? 4. Область определения функции f(х) состоит из всех положительных чисел. Может ли эта функция быть четной? 5. Является ли данная функция четной? x2-2|x| ОТВЕТЫ Сравните f(2) и f(-3) 2. Начертите эскиз графика функции возрастающей на [-1;2] и [5;7], убывающей на [2;5] 3. Какие из функций y=78x, y=x, y=x3, y=x2, y=2x-9 являются на (-; 0) убывающими? 4. Область определения функции f(х) состоит из всех отрицательных чисел. Может ли эта функция быть нечетной? 5. Является ли данная функция нечетной? x|x| +2x ОТВЕТЫ 1. f(3)<f(5) 2. 1. f(2)<f(-3) 2. y y 3 x 2 5 3. y=x3, y=2x-9 4. Нет 5. Да 3. y=7-8x, y=x2 4. Нет 5. Да 4. Индивидуальные задания (4 чел.). Построить графики функций: 1) y=(2x+1)/(x-1); 2) y=x+2 при x<=-1, y=x2 при x>-1; 3) y=x|x|-2x; 4) y=(4-x)/(1-x). Определите по графику: - D(f); - промежутки возрастания и убывания; - точки экстремума; - M и m; - Е(f); x - Промежутки знакопостоянства (f(x)>=0, f(x)<=0). Карточки “Линейная функция и ее график” (2 чел.) Компьютерное тестирование “Функции и их свойства” (8 чел.) Тестирование производится в автоматизированной обучающей системе “Диалог” (2 варианта, 8 заданий). 5. Работа с доски. I. Найдите Е(f): 1. y=x2+x-20 2. y=(x-4)2+9 3. y=(x-7)2-2 4. y=5/(x-2) 5. y=|x-4|-2 6. y=5-((2x+1) 1. y>=-20,25 2. y>=9 3. y>=-2 4. (-; 0)U(0;+) 5. [-2;+) 6. (-; 5] II. Найдите М и значение аргумента, при котором достигается это М. а) y=5-|x+8|; b) y=2-(x-2); M=5 M=2 x=-8 x=2 Найдите m и значение аргумента, при котором достигается это m. с) y=(4x2-12x+9) - 2; d) y=3+(x2-3x+2). m=-2 m=3 4x2-12x+9=0 x2-3x+2=0 D=144-4*4*9=0 x1=2, x2=1 x=1,5 III. Начертил ученик графики функций y=x3 и y=x5, потом стер оси координат. Назовите координаты точек А, В, С. Графиком какой из них является линия I, II? A(-1;-1); B(0;0); C(1;1). I) y=x3; II) y=x5. IV. Докажите, что линия на рисунке не является графиком функции y=2x4-x2-1 y x f(0)=-1, а на графике нет точки (0;-1). №№114 (а, б), 116 (а, б), 117 (а, б), 119 (а, б); сборник: п. 8, №№142, 147. 6. Работа по учебнику: № 114 (а, б) - 2 человека одновременно (предварительно обсудив) № 116 y-2x+1<=0, y-2x+1=0 y=2x-1 y=ax2+3x+2, y y=2x-1 x № 116 (а) y-2x-1<=0, y y=2x+1 y=ax2+3x+2 x y=2x+1, y-2x-1=0 ax2+3x+2 a>1/4 a>0, ветви вверх ax2+3x+2=2x+1; ax2+3x+2-2x-1=0; ax2+x+1=0. D=1-4a, если D<0, то нет общих точек: 1-4a<0; -4a<-1; a>1/4 №116 (б) y-3x+1>=0, y=ax2-4xax2-4x-3 a<-6,125 a<0, ветви вниз ax2-4x-3=3x-1; ax2-7x-2=0. D=49+8a; 49+8a<0; 8a<-49; a<-6,125 y y-3x+1=0 x 3, y=3x-1 №117 (а) y a) y=-x2+2x+2, x[0; 2] x0=-b/2a=-(2/-2)=1, y0=-1+2+2=3; (1,3) вершина параболы, ветви вниз; x x=1 - точка максимума ymax=3, M=3. y[2; 3] b) y=x2-3x+1, x[0; 2] x0=-b/2a =-(-3/2)=1,5, y0=9/4-9/2+1=-1,25; (1,5; -1,25) - вершина, ветви направлены вверх; y x m=-1,25, M=1. y[-1,25; 1] 7. Итоги урока. Домашнее задание. № 26, стр. 145 (без графика), № 30 (Шуба М.Ю.) y=x2-6x+5. Резерв: Запишите функцию, графиком которой является парабола ax 2+bx+c, ее ветви опущены вниз (a<0), проходит через точку (-1;-8). (-8=-a-b+c)