a a Âèä ñïåðåäè 1 2 2 Âèä ñâåðõó F) I I зарядов, и сравните ее с
реклама

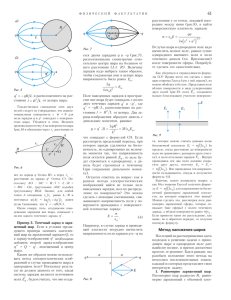
46 Ê Â À Í T 2001/№4 çàðÿäîâ, è ñðàâíèòå åå ñ ñèëîé Àìïåðà. Óêàçàíèå. Íàïðÿæåííîñòü ýëåêòðè÷åñêîãî ïîëÿ âáëèçè çàðÿæåííîé áåñ1 q êîíå÷íîé íèòè ðàâíà E = , ãäå 2πε0 r q çàðÿä åäèíè÷íîé äëèíû íèòè, r ðàññòîÿíèå äî íèòè. Ñíà÷àëà âû÷èñëèì êîíöåíòðàöèþ ýëåêòðîíîâ ïðîâîäèìîñòè â ìåäè: n= ρNA = 0,84 ⋅ 1029 ì −3 A è ñèëó òîêà â ïðîâîäàõ: πd I= 2 4 nev = 42,2 A (çäåñü å çàðÿä ýëåêòðîíà). Òåïåðü, âîñïîëüçîâàâøèñü ôîðìóëîé ( ), íàéäåì âåëè÷èíó èíäóêöèè ìàãíèòíîãî ïîëÿ, ñîçäàâàåìîãî òîêîì îäíîãî èç ïðîâîäîâ â ìåñòå ðàñïîëîæåíèÿ âòîðîãî: B= µ0I 2 πL Îòíîøåíèå ñèëû ìàãíèòíîãî âçàèìîäåéñòâèÿ ê ýëåêòðîñòàòè÷åñêîé ñèëå â ïðåäåëàõ ïîãðåøíîñòè ðàñ÷åòà äàåò FA −23 = 1,1 ⋅ 10 . Fý Çàäà÷à 2. Íà íåïðîâîäÿùåé ãîðèçîíòàëüíîé ïîâåðõíîñòè ñòîëà ëåæèò ïðîâîäÿùàÿ æåñòêàÿ òîíêàÿ ðàìêà èç îäíîðîäíîãî êóñêà ïðîâîëîêè â âèäå ðàâíîñòîðîííåãî òðåóãîëüíèêà ñî ñòîðîíîé à. Ðàìêà íàõîäèòñÿ â îäíîðîäíîì ãîðèçîíòàëüíîì ìàãíèòíîì ïîëå, ëèíèè èíäóêöèè êîòîðîãî ïåðïåíäèêóëÿðíû îäíîé èç ñòîðîí ðàìêè. Ìàññà ðàìêè m, âåëè÷èíà èíäóêöèè Â. Êàêîé òîê íóæíî ïðîïóñòèòü ïî ðàìêå (ïðîòèâ ÷àñîâîé ñòðåëêè), ÷òîáû îíà íà÷àëà ïðèïîäíèìàòüñÿ îòíîñèòåëüíî îäíîé èç âåðøèí òðåóãîëüíèêà? Ïóñòü ïî êîíòóðó ïðîòèâ ÷àñîâîé ñòðåëêè òå÷åò òîê I (ðèñ.4). Î÷åâèäíî, ÷òî íà âñå òðè ñòîðîíû òðåóãîëüíèêà = 1,7 ⋅ 10 −4 Òë . D P P′ Íà ðèñóíêå 3 èçîáðàæåíà îäíà èç ëèíèé èíäóêöèè ìàãíèòíîãî ïîëÿ ïðî- I F), I I O F) A I F)+ B Рис. 3 C I Рис. 4 âîäà. Ñèëà Àìïåðà, äåéñòâóþùàÿ íà ýëåìåíò ïðîâîäà, ðàâíà 2 FA = BIl = µ0I l 2 πL = 7,13 ⋅ 10 −3 H. Äëÿ âû÷èñëåíèÿ ýëåêòðîñòàòè÷åñêîé ñèëû íàéäåì çàðÿä q ýëåêòðîíîâ, ñîäåðæàùèõñÿ â êóñêå ïðîâîäà åäèíè÷íîé äëèíû: q= πd 2 4 ne = 4,22 ⋅ 10 4 Êë . → Íàïðÿæåííîñòü ýëåêòðè÷åñêîãî ïîëÿ, ñîçäàâàåìîãî ýëåêòðîíàìè, ðàñïîëîæåííûìè âäîëü ïðîâîäà, íà ðàññòîÿíèè L îò ïðîâîäà ðàâíà E= áóäóò äåéñòâîâàòü ñèëû Àìïåðà, òî÷êàìè ïðèëîæåíèÿ êîòîðûõ ÿâëÿþòñÿ ñåðåäèíû ñòîðîí ÀÑ, CD è DA.  òî÷êå ïåðåñå÷åíèÿ ìåäèàí (òî÷êà Î) ïðèëîæåíà ñèëà òÿæåñòè, ðàâíàÿ mg è íàïðàâëåííàÿ îò íàñ ïåðïåíäèêóëÿðíî ïëîñêîñòè ðèñóíêà. Íàéäåì ðåçóëüòèðóþùèé ìîìåíò ñèë Àìïåðà, äåéñòâóþùèõ íà òðè ñòîðîíû òðåóãîëüíèêà, îòíîñèòåëüíî îñè PP ′ . → Ñèëà FAC ðàâíà FAC = IaB è íàïðàâ- q 2 πε 0 L = 1,5 ⋅ 10 16  ì, à ýëåêòðîñòàòè÷åñêàÿ ñèëà îòòàëêèâàíèÿ, äåéñòâóþùàÿ íà ýëåìåíò ïðîâîäà åäèíè÷íîé äëèíû, çàðÿæåííûé ýëåêòðîíàìè ïðîâîäèìîñòè, ñîñòàâëÿåò Fý = qE = 6,3 ⋅ 10 20 H. Âèäíî, ÷òî ñ óâåëè÷åíèåì òîêà ìîìåíò ñèë Àìïåðà óâåëè÷èâàåòñÿ è â íåêîòîðûé ìîìåíò îêàæåòñÿ â ñîñòîÿíèè ïðèïîäíÿòü ðàìêó îòíîñèòåëüíî âåðøèíû D, ïîñêîëüêó ïðåïÿòñòâóåò ýòîìó ïîñòîÿííûé ìîìåíò ñèëû òÿæåñòè a M g = mg ⋅ . 3 Ðàìêà íà÷íåò ïðèïîäíèìàòüñÿ îòíîñèòåëüíî âåðøèíû D, êîãäà M A ≥ M g , èëè 3 4 2 Ia B ≥ mg a 3 . Îòñþäà 4 mg . 3aB Çàäà÷à 3. Íà íåïðîâîäÿùåé ãîðèçîíòàëüíîé ïîâåðõíîñòè ñòîëà ëåæèò ïðîâîäÿùàÿ òîíêàÿ æåñòêàÿ êâàäðàòíàÿ ðàìêà èç îäíîðîäíîãî êóñêà ïðîâîäà ñî ñòîðîíîé à. Ðàìêà íàõîäèòñÿ â ìàãíèòíîì ïîëå äëèííîãî ãîðèçîíòàëüíîãî ïðîâîäà ñ òîêîì, ðàñïîëîæåííîãî ñèììåòðè÷íî íàä ðàìêîé (ðèñ.5). Ìàññà ðàìêè m, èíäóêöèÿ ìàãíèòíîãî ïîëÿ ó áîêîâûõ ñòîðîí ðàìêè 1 è 2 ðàâíà Â, êîýôôèöèåíò òðåíèÿ ñêîëüæåíèÿ ðàìêè î ïîâåðõíîñòü ñòîëà µ ( µ < 1 3 ). Êàêîé òîê íóæíî ïðîïóñòèòü ïî ðàìêå, ÷òîáû îíà íà÷àëà ñêîëüçèòü ïî ñòîëó, íå îòðûâàÿñü îò íåãî? Ïóñòü ïî êâàäðàòíîé ðàìêå òå÷åò òîê I ïî ÷àñîâîé ñòðåëêå, åñëè ñìîòðåòü ñâåðõó. Íà áîêîâûå ñòîðîíû ðàìêè → áóäóò äåéñòâîâàòü ñèëû Àìïåðà F1 è I≥ Âèä ñïåðåäè a 2 1 2 Âèä ñâåðõó → ëåíà íà íàñ, ñèëû FAD è FDC ðàâíû > C FAD = FDC = IaB sin α 2 = IaB 2 o (ïîñêîëüêó α = 60 ) è íàïðàâëåíû îò íàñ. Ñóììàðíûé ìîìåíò âñåõ òðåõ ñèë Àìïåðà îòíîñèòåëüíî îñè PP ′ ðàâåí M A = IaB ⋅ 3 2 a− IaB 2 IaB 2 ⋅ 3 4 ⋅ 3 4 a= a a− 3 4 2 Ia B . Рис. 5