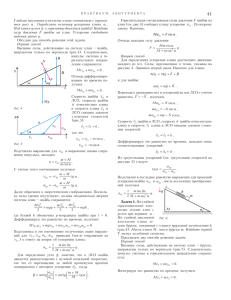
Ïóñòü «ïîëîâèíà îñòàâøåãîñÿ ïóòè» ñîñòàâëÿåò x. Òîãäà + x v
реклама

ÇÀÄÀ×ÍÈÊ «ÊÂÀÍÒÀ» Ïóñòü «ïîëîâèíà îñòàâøåãîñÿ ïóòè» ñîñòàâëÿåò x. Òîãäà âòîðàÿ ïîëîâèíà âðåìåíè ïîåçäêè ðàâíà x v2 + x v3 , à âñå ðàññòîÿíèå ìåæäó ãîðîäàìè ðàâíî 2x + v1 x v2 + x v3 . Îñòàëîñü ðàçäåëèòü ýòó âåëè÷èíó íà ïîëíîå âðåìÿ ïîåçäêè 2 x v2 + x v3 è ñîêðàòèòü íà õ.  ðåçóëüòàòå äëÿ èñêîìîé ñðåäíåé ñêîðîñòè ïîëó÷àåì v 2v 3 v vcp = + 1 ≈ 54,3 êì/÷. 2 v2 + v3 Ç.Ðàôàèëîâ Óäîáíî òåïåðü óñêîðåíèå òåëåæêè ïðåäñòàâèòü â âèäå ñóììû äâóõ ïåðïåíäèêóëÿðíûõ ñîñòàâëÿþùèõ âäîëü è ïîïåðåê íàêëîííîé ïëîñêîñòè, ðàâíûõ Ô1669. Íà ãîðèçîíòàëüíîé ïîâåðõíîñòè ïîêîèòñÿ ãëàäêèé êëèí ìàññîé Ì ñ óãëîì α ïðè îñíîâàíèè. Êóá òàêîé æå ìàññû ëåæèò íà m ñòîëå, êàñàÿñü êëèíà (ðèñ.1). Êîýôôèöèåíò òðåíèÿ ìåæäó êóáîì è ñòîëîì M M µ µ . Íà êëèí ñòàâÿò α òåëåæêó ìàññîé m, Ðèñ.1 êîòîðàÿ ìîæåò ñêîëüçèòü ïî êëèíó áåç òðåíèÿ, è îòïóñêàþò. Êàêóþ ñêîðîñòü ïðèîáðåòåò òåëåæêà, îïóñòèâøèñü íà âûñîòó h (ïðè ýòîì îíà âñå åùå íàõîäèòñÿ íà ïîâåðõíîñòè êëèíà)? b èëè, ïîñëå ïîäñòàíîâêè çíà÷åíèé äëÿ à è b, c b h g Åñëè ñèëà òðåíèÿ äîñòàòî÷íà äëÿ óäåðæàíèÿ ñèñòåìû íà ìåñòå, òî ñêîðîñòü òåëåæêè áóäåò ðàâíà v = ýòîì ñïðàâåäëèâû ñîîòíîøåíèÿ 2 gh . Ïðè N = mg cos α è N sin α = Fòð ≤ µMg , ãäå N ñèëà ðåàêöèè, äåéñòâóþùàÿ íà òåëåæêó ñî ñòîðîíû êëèíà. Åñëè æå ñèëà òðåíèÿ íåäîñòàòî÷íàÿ, â äâèæåíèå ïðèäóò âñå òåëà ñèñòåìû. Ïðåäñòàâèì óñêîðåíèå òåëåæêè â âèäå ñóììû (âåêòîðíîé) äâóõ óñêîðåíèé (ðèñ.2): óñêîðåíèÿ N a a b α a mg Ðèñ.2 → a , ñ êîòîðûì òåëåæêà äâèæåòñÿ âìåñòå ñ êëèíîì, è → óñêîðåíèÿ b îòíîñèòåëüíî êëèíà. Çàïèøåì óðàâíåíèÿ âòîðîãî çàêîíà Íüþòîíà äëÿ òåëåæêè, â ïðîåêöèÿõ íà íàïðàâëåíèÿ âäîëü êëèíà è ïåðïåíäèêóëÿðíî åìó, è äëÿ êëèíà âìåñòå ñ êóáîì, â ïðîåêöèÿõ íà ãîðèçîíòàëüíîå íàïðàâëåíèå: mg sin α = m b − a cos α , mg cos α − N = ma sin α , b g N sin α − µMg = 2 Ma . Èñêëþ÷àÿ N, íàõîäèì a=g m sin α cos α − µM 2 2 M + m sin α b = g sin α ⋅ 2 M + m − µM ctg α 2 2 M + m sin α Âðåìÿ äâèæåíèÿ òåëåæêè âíèç ðàâíî τ= 6 Êâàíò ¹2 , 2h b sin α . . a1 = b − a cos α = g sin α è a2 = a sin α . Òîãäà äëÿ ñêîðîñòè òåëåæêè ïîëó÷àåì v= ca τh + ca τh = = τ b g sin α g + ba sin α g 2 1 2 2 2 v= b 2 = 2h sin α 2 gh m sin α cos α − µM g g 2 + a2 , b2 M + m − µM ctg α ge2 M + m sin α j 2 . À.Êëèíîâ Ô1670. Êîìíàòà ïëîùàäüþ S = 20 ì 2 ñ âûñîòîé ïîòîëêà Í = 3 ì çàïîëíåíà âîçäóõîì ïðè íîðìàëüíûõ óñëîâèÿõ. Îöåíèòå ÷èñëî óäàðîâ ìîëåêóë î ïîòîëîê çà âðåìÿ τ = 1 ÷. Êóäà ÷àùå óäàðÿþò ìîëåêóëû â ïîë èëè â ïîòîëîê êîìíàòû? Îöåíèòå ðàçíîñòü ÷èñåë óäàðîâ ìîëåêóë î ïîë è î ïîòîëîê çà âðåìÿ τ . Ñ÷èòàéòå òåìïåðàòóðó âîçäóõà â êîìíàòå ïîâñþäó îäèíàêîâîé. Ïóñòü vz «ñðåäíÿÿ» ïðîåêöèÿ ñêîðîñòè ìîëåêóëû íà íàïðàâëåíèå «ê ïîòîëêó», nêîíöåíòðàöèÿ ìîëåêóë. Òîãäà ÷èñëî óäàðîâ ìîëåêóë î ïîòîëîê çà âðåìÿ τ áóäåò Nóä = 0,5 nvz Sτ . Îöåíèì vz ïî ñðåäíåìó êâàäðàòó ñêîðî- ñòè ìîëåêóëû (íå çàáûâàÿ âçÿòü îò ýòîãî çíà÷åíèÿ îäíó òðåòü): RT vz = ≈ 3 ⋅ 102 ì ñ , Μ ãäå òåìïåðàòóðà âîçäóõà T ≈ 300 Ê, à ñðåäíÿÿ ìîëÿðíàÿ ìàññà âîçäóõà Ì = 0,029 êã/ìîëü. Êîíöåíòðàöèþ íàéäåì èç ñîîòíîøåíèÿ p n= ≈ 2,5 ⋅ 1025 ì −3 , kT ãäå äàâëåíèå âîçäóõà p ≈ 10 5 Ïà, à ïîñòîÿííàÿ Áîëüöìàíà k = 1,38 ⋅ 10 −23 Äæ Ê . Òàêèì îáðàçîì, Nóä = 0,5nv z Sτ ≈ 2,5 ⋅ 10 32 . Ðàçíîñòü ÷èñåë óäàðîâ î ïîë è ïîòîëîê ïðè íåèçìåííîé òåìïåðàòóðå îïðåäåëÿåòñÿ ðàçíîñòüþ êîíöåíòðàöèé ìîëåêóë (ó ïîëà äàâëåíèå âûøå íà ∆p = ρgH = pΜ gH RT : Nóä ∆p N óä ΜgH 1 29 ∆Nóä = = ≈ 10 ≈ Nóä . p 4000 RT Ð.Àëåêñàíäðîâ b g Ô1671. Òðè ïàðàëëåëüíûõ òîíêèõ íåïðîâîäÿùèõ ñòåð- æíÿ íàõîäÿòñÿ â ãîðèçîíòàëüíîé ïëîñêîñòè; ðàññòîÿíèå ìåæäó ñîñåäíèìè ñòåðæíÿìè d (ñì. ðèñóíîê). Íà ñòåðæíè íàñàd L æåíû òÿæåëûå øàéáû ìàññîé Ì êàæäàÿ, çàðÿd æåííûå îäèíàêîâûìè çàðÿäàìè Q.  íà÷àëüíûé ìîìåíò òðè èç íèõ íåïîäâèæíû è íàõîäÿòñÿ íà ïðÿìîé, ïåðïåíäèêóëÿðíîé ñòåðæíÿì, à ÷åòâåðòàÿ äâèæåòñÿ èçäàëè ïî ñðåäíåìó ñòåðæíþ ñî ñêîðîñòüþ