task_13437

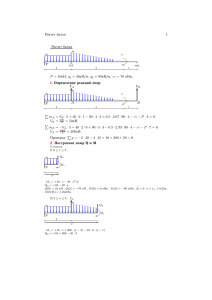
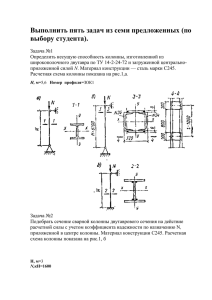
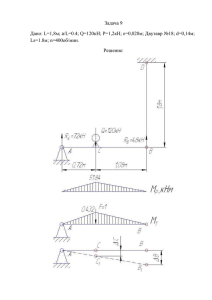
Суть того что надо сделать:
Изменить исходные данные и произвести расчеты
задачи выделеные красно-черным цветом,
За остальные цвета прошу прощения,
это - «фантазия преподавателя».
Инструкция продвинутому студенту!
Студент
должен
изучить
задачи,
законспектировать
собственной ручонкой (переписать). В каждой задаче по своему
решению изменить исходные данные и произвести расчеты
5 семестр. Основы функционирования
машин и их элементов в системе
промышленного сервиса
Теоретическая механика это наука, в которой
изучаются общие законы механического движения и механического
взаимодействия материальных тел.
Раздел 1.Статика- это
раздел механики, в котором
изучаются методы преобразования систем сил в эквивалентные системы
и устанавливаются условия равновесия сил, приложенных к твердому
телу.
Сила - это мера механического взаимодействия тел, определяющая
интенсивность и направление этого взаимодействия. Сила определяется
тремя элементами: числовым значением (модулем), направлением и
точкой приложения. Сила изображается вектором.
Реакцией связи называется сила или система сил, выражающая
механическое действие связи на тело.Одним из основных положений
механики является пpuнцип освобождаемости т тел от связей, согласно
которому несвободное твердое тело можно рассматривать как свободное, на
которое кроме задаваемых сил действуют реакции связей.
2
( Задача №1 )
З А ДАЧ А 1 . Определение реакций опор составной
конструкции
Конструкция состоит из двух тел, соединенных шарнирно в точке С.
Тело АС закреплено с помощью заделки, тело ВС имеет шарнирноподвижную (скользящую) опору (рис. 1). На тела системы действуют
распределенная по линейному закону сила с максимальной интенсивностью
qтах = 2 кН/м, сила F = 4 кН под углом α = 30o и пара сил с моментом М = 3
кНм. Геометрические размеры указаны в метрах. Определить реакции опор и
усилие, передаваемое через шарнир. Вес элементов конструкции не
учитывать.
Рис. 1
Рис. 2
Решение.Если рассмотреть равновесие всей конструкции в целом,
учитывая, что реакция заделки состоит из силы неизвестного направления и
пары, а реакция скользящей опоры перпендикулярна опорной поверхности,
то расчетная схема будет иметь вид, представленный на рис. 2.
Здесь равнодействующая распределенной нагрузки
1
1
Q  qmax  6   2  6 кН
2
2
расположена на расстоянии двух метров (1/3 длины AD) от точки А; МА —
неизвестный момент заделки.
В данной системе сил четыре неизвестных реакции (ХА, YA, MA, RB), и
их нельзя определить из трех уравнений равновесия плоской произвольной
системы сил.
Поэтому расчленим систему на отдельные тела по шарниру (рис.3).
3
Рис. 3
Силу, приложенную в шарнире, следует при этом учитывать лишь на
одном теле (любом из них). Уравнения для тела ВС:
x :  X C  RB  0;
y :  YC  0;
M C : M  RB  3  0.
Отсюда ХС = – 1 кН; УС = 0; RB = 1 кН.
Уравнения для тела АС:
x : X A  Q  F cos   X C  0;
y : YA  F sin   YC  0;
M A : M A  Q  2  F cos   6  F sin   2  YC  2  X C  6  0.
Здесь при вычислении момента силы F относительно точки А
использована теорема Вариньона: сила F разложена на составляющие Fcos α
и Fsin α и определена сумма их моментов.
Из последней системы уравнений находим:
ХА = – 1,54 кН; УА = 2 кН; МА = – 10,8 кНм.
Для проверки полученного решения составим уравнение моментов сил
для всей конструкции относительно точки D(рис. 2):
M
Di
 M A  X A  6  Q  4  F sin   2  M  RB  3 
 10,8  9,24  24  4  3  3  27,04  27  0.
Вывод: проверка показала, что модули реакций определены верно. Знак
минус у реакций говорит о том, что реально они направлены в
противоположные стороны.
4
Раздел 2. Кинематика это раздел механики,
в котором
изучается движение материальных тел в пространстве с
геометрической точки зрения, вне связи с силами, определяющими это
движение.
Скорость — это векторная величина, характеризующая быстроту и
направление движения точки в данной системе отсчета.
При неравномерном криволинейном движении точки изменяются
модуль и направление ее скорости. Ускорение точки характеризует быстроту
изменения модуля и направления скорости точки.
Поступательным движением твердого тела называется такое движение, при котором любая прямая, проведенная в теле, остается во все время
движения тела параллельной своему начальному положению.
Все точки твердого тела. движущегося поступательно описывают
одинаковые (совпадающие при наложении) траектории и в каждый момент
времени имеют геометрически равные скорости и ускорения.
Вращательным движением твердого тела называется такое его
движение, при котором все точки, принадлежащие некоторой прямой,
неизменно связанной с телом, остаются неподвижными.
Величина, характеризующая быстроту изменения угла поворота φ с
течением времени, называется угловой скоростью тела.
~ 
d
  .
dt
Числовая величина, характеризующая быстроту изменения угловой
скорости с течением времени, называется угловым ускорением тела.
5
( Задача №2 )
Задача 1. Определение кинематических
характеристик поступательного и вращательного движений твердого
тела
Груз 1 (рис. 1), опускаясь, согласно уравнению s = 3 t 3 +15, где s - расстояние
груза от места схода нити с поверхности вала в сантиметрах; t - время в секундах,
приводит в движение колесо 2, ременную передачу, колесо 3 и рейку 4.
Рис.1
Пренебрегая скольжением ремня по ободам колес, определить для момента
времени t1 =1 с скорость и ускорение рейки 4, угловые скорости и ускорения колёс 2, 3
и ускорение точки А, если r2 =30 см; R2 =50 см - радиусы ступеней колеса 2; r3 =40 см;
R3 =60 см - радиусы ступеней колеса 3.
Дано: s  3t 3  15 ; r2 =30
см; R =50 см;
2
R3 =60
см.
Определить: V4 , a4 , 2 , 3 ,  2 ,  3 , aA при t1  1 с.
1. Найдём
2 , 3 . Зная уравнение движения груза 1, определим его скорость
V1 = s = 9 t 2 . Груз подвешен на нерастяжимом канате,
поэтому скорость груза 1 такая же, как скорости точек на ободе колеса 2 радиуса r2 ,
как функцию времени
2
т.е. VB  V1  9t . Найдем 2 как функцию времени:
VB 9t 2
2  
 0,3t 2 .
r2
30
(а)
Так как колёса 2 и 3 связаны ременной передачей (ремень нерастяжим), то
VE  VM , но VE  2  R2 ; VM  3 R3 .
2 R2  3 R3 ,
6
поэтому
3 
2 R2
R3
0,3t 2  50

 0, 25t 2 .
60
При t=1 с из (а) и (б) найдем
=
0,3 рад/с;
(б)
=0,25 рад/c.
2. Определим V4 . Так как V4 = VD  3r3 , то при t1 =1 с имеем V4 =10 см/c.
3. Найдем  2 ,  3 . Продифференцируем по времени выражения (а), (б):
 2  2  0, 6t ;  3  3  0,5t . При t1 =1с  2 =0,5 рад/ c .
2
4. Найдем a4 . Рейка 4 движется поступательно, поэтому все её точки имеют
одинаковые ускорения. Точка D одновременно принадлежит рейке 4 и ободу колеса 3

радиуса r3 , поэтому a4  aD   3r3 ; при t1 =1с и a4 =20 см/ c 2
5. Найдем
ускорение
вращательное ускорение;
При t1 =1с и
точки
А,
используя
формулу
aA   2 R2 -
a An  22 R2 .-центростремительное ускорение.
aA =30 см/ c ; a An =4,5 см/ c
2
2
;
aA  (aA )2  (aAn )2  30,34 см/ c 2 .
7
Раздел 3. Динамика раздел
механики, в котором
изучается движение материальных тел в пространстве в зависимости от
действующих на них сил.
( Задача №3 )
Задача 1. ПРИМЕНЕНИЕ ТЕОРЕМЫ ОБ
ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ К ИССЛЕДОВАНИЮ
ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
Каток для раскатывания асфальта (рис. 1) состоит из кузова массой т1
= 3∙103 кг и двух одинаковых барабанов. Масса барабана m2=103 кг, радиус
его r=0,5м, а радиус инерции ρ=0,4м. Коэффициент трения качения
барабанов fк=9 см. Определить скорость кузова катка после того, как он
проехал расстояние S=2 м, начальная скорость катка была равна 0,2 м/с. К
ведущему барабану приложен постоянный момент M=4,6 кНм.
Рис. 1
Рис. 2
Решение. Так как в задаче идет речь о конечном перемещении
системы, то следует применить теорему об изменении кинетической энергии
в интегральной (конечной) форме:
n
T  T0  
i 1
Aie
n
  Ai j .
i 1
8
Кинетическая энергия системы (поступательно движущийся кузов и
совершающие плоское движение барабаны) имеет вид
1
1
1

T  m1v 2  2 m2vC2  J zC 2  ,
2
2
2

где v — скорость кузова, vС — скорость центра масс барабана, ω — его
угловая скорость, JzC = m2ρ2 = 160 кгм2 — момент инерции барабана
относительно его оси (проходящей через центр масс).
Кинематические связи определяются тем, что каждый барабан
поворачивается вокруг своего мгновенного центра скоростей (точки Р), а
именно: vC = ωr; кроме того, v = vC, т. е. ω = v/r. Тогда кинетическая
энергия приводится к виду
1
T  mnp v 2 ,
2
где тпр= 6280 кг — приведенная к кузову масса системы. Начальная
кинетическая энергия системы
T0 
1
mnp v02  125,6 Дж.
2
Вычислим теперь величину работы действующих сил (рис. 2).
Внешние силы. Силы тяжести барабанов G2 и кузова G1 работы не
совершают, поскольку они перпендикулярны скоростям (и, соответственно,
перемещениям) точек их приложения. Также не работают нормальные
'
реакции Rn и R’n и силы трения Frp и Fmp , так как всегда равны нулю
скорости их точек приложения — мгновенных центров скоростей, и,
соответственно, постоянно равны нулю их мощности.
Работу будут совершать моменты сопротивления качению:
'
M ск  f к Rn и M ск
 f к Rn' ,
а именно:
 Aie  M ск  М ск'    f к ( Rn  Rn' ) ,
где
Rn  Rn'  G1  2G2 .
9
Здесь φ — угол поворота барабанов, для которого, интегрируя
уравнение кинематической связи ω = v/r с учетом нулевых начальных
условий для перемещений s и φ, легко получаем φ = s/r. Тогда
s
r
 Aie   f к (G1  2G2 ) .
Внутренние силы. Запишем, учитывая, что кузов не вращается,
суммарную работу внутренних сил (моментов) М и М’:
 Ai j  M  M '0  M
s
.
r
Тогда сумма работ всех сил запишется в виде
1
r
 Ai   Aie   Ai j  ( M  f к (G1  2G2 )) s .
Множитель, стоящий в этой формуле перед перемещением s, — это
приведенная сила системы
Итак
1
Fnp  ( M  f к (G1  2G2 ))  380 H .
r
 Ai  Fnp s  760 Дж.
Собирая правую и левую части теоремы, получаем
T  T0   Ai
или Т – 125,6 = 760, откуда
2  885,6
1
T  mnp v 2  885,6 Дж и v 
 0,53 м / с.
2
6280
Ответ: v = 0,53 м/с.
10
6 семестр. Основы расчета механизмов и машин.
Сопротивление материалов— это наука об инженерных
методах расчета на прочность, жесткость и устойчивость элементов
конструкций.
Способность конструкции (или отдельного ее элемента)
выдерживать заданную нагрузку не разрушаясь и без появления
остаточных деформаций называют прочностью.
Способность конструкции (или отдельного элемента) сохранять
исходную форму в заданных (обычно весьма малых) пределах
называется жесткостью.
Способность конструкции (или отдельного элемента) сохранять
первоначальную форму упругого равновесия называют устойчивостью.
Чтобы правильно рассчитать конструкцию на прочность или на
жесткость, необходимо уметь определять внутренние силы по нагрузке. Для
выявления внутренних сил в сопротивлении материалов применяется
метод сечений.
Правила знаков внутренних силовых факторов (ВСФ).
1. Продольная сила N считается положительной, если она
вызывает растяжение отсеченной части и отрицательной, если
вызывает ее сжатие.
2. Поперечная сила Q считается положительной, если она вращает
отсеченную часть по ходу часовой стрелки и отрицательной, если
вращение происходит против хода часовой стрелки.
11
3. Изгибающий момент положителен, если сжаты верхние
волокна отсеченной части, и отрицателен, если сжаты нижние волокна.
Эпюра изгибающих моментов строится на сжатых волокнах.
4. Правило знаков для крутящего момента удобно принимать
произвольным.
Интенсивность, равная величине внутренних сил, приходящихся на
единицу площади называется напряжением в точке и является ключевым
понятием в сопромате. Напряжения измеряются в Н/м2 (Па) и МПа.
Существует 2 вида напряжений:

Qy
Q
dN
; y 
; x  x ,
dF
dF
dF
причем  (сигма) — нормальное напряжение, действует по нормали
(перпендикуляру) к площадке;
 (тау) — касательные напряжения, они скользят по площадке,
касаются ее .
В сопромате различают несколько простых видов нагружения и
несколько сложных. К простым относятся следующие.
Центральное растяжение (сжатие) возникает в случае, когда
стержень нагружен силами, совпадающими по направлению с его осью В
этом случае из шести внутренних силовых факторов пять равны нулю и
только продольная сила
N  0.
На растяжение, сжатие работают многие элементы конструкций:
стержни ферм, колонны, штоки паровых машин и поршневых насосов,
стяжные винты, канаты лебедок и другие детали.
12
Сдвиг или срез возникает, когда внешние силы смещают два
параллельных сечения одно относительно другого, при неизменном
расстоянии между ними. На сдвиг или срез работают, например, заклепки
или болты, скрепляющие элементы, которые внешние силы пытаются
сдвинуть
Кручение возникает при действии на стержень внешних сил,
образующих моменты относительно продольной оси стержня. При этом
из шести внутренних сил только
M кр  0 .
На кручение работают
валы, шпиндели токарных и сверлильных станков, роторы двигателей и
другие детали
Изгиб — это такой вид нагружения, когда внешние силы вызывают
моменты относительно оси симметрии (или главной оси), расположенный
в плоскости поперечного сечения. Этот момент называется изгибающим.
Самый простой случай — это плоский изгиб, когда все внешние силы лежат
в одной плоскости, совпадающей во всех рассматриваемых нами случаях с
плоскостью симметрии (или главной плоскостью) балки.
Расчеты на прочность выполняются в напряжениях:
нормальных —  или касательных —  . Оценка прочности конструкции
сводится к сравнению расчетных напряжений с допускаемыми:
 max   ;
(1.1)
 max   .
(1.2)
Это и есть основные условия прочности, в которых в правой части
всегда стоит допускаемое напряжение, а в левой — максимальное
рабочее напряжение, иногда его называют «расчетным».
13
( Задача №4 ) Задача 1. Расчет на прочность бруса
при
растяжении
14
15
16
17
18
( Задача №5 )
Задача 2. Расчет вала на прочность при
кручении
19
20
21
22
( Задача №6 ) Десерт =)
« Здесь можно токо каплю изменить,
а если слишком мудреная можно не трогать»
Задача 3. Расчет балки на изгиб
23
24
Для балки ( рис. 3, а) построить эпюры поперечных сил и изгибающих
моментов. Из расчета на прочность по нормальным напряжениям подобрать
номер двутавра. Проверить прочность выбранного двутавра по главным
напряжениям, используя третью теорию прочности.
Исходные данные: F=60 кН; M=70 кНм; q=40 кН/м; а=1 м; b=3 м; с=2
м; [σ]=155 МПа.
25
Рис. 3 Решение.
1. Определим реакции опор Y A и YB , составив для этого уравнения
равновесия:
a2
c
 M A  0; F  a q  2  m  q  c  (b  2 )  YB  (b  c)  0 ;
c
1
q  c(b  )  Fa  qa2  m 40  2  4  60  1  40  0.5  70
2
2
YB 

 34 кН ;
bc
5
a
qc2
 M B  0; F (a  b  c)  qa  ( 2  b  c)  2  m  YА (b  c)  0 ;
a
c2
F (a  b  c)  qa(  b  c)  q  m 60  6  40  5.5  40  2  70
2
2
YA 

 146 кН
bc
5
2. Сделаем проверку:
 y  0;
YA  YB  q  a  q  c  F  0;146  34  40  1  40  2  60  0.
Реакции найдены правильно.
3.Построение эпюр.
Для построения эпюр разобьём балку на три участка и составим
уравнение для Q и М.
I участок: 0  z  a.
26
Q I   F  qz; M I   Fz  q
При z=0
При z=a
z2
;
2
Q I   F  60 кН ; M1  0.
Q I   F  qa  100 кН ;
M I   Fa  q
a2
 80 кН  м.
2
II участок: a  z  (a  b) .
Q II   F  qa  YA  46 кН ;
a

M II   Fz  qa z    YA  z  a .
2

При z=a
При z=a+b
a2
 80 кН  м.
2
a

M II   F a  b   qa b    YAb  58 кН  м.
2

M II   Fa  q
III участок: 0  z1  c .
z12
Q  YB  qz1; M
 m  YB z1  q .
2
III
III
Q  YB  34 кН ; M  m  70 кНм .
III
При z1=0
III
c2
Q  YB  qc  46 кН ; M
 m  YB  c  b
 58 кНм .
При z1=с
2
На этом участке график поперечной силы пересекает ось эпюры (рис.
III
III
3, б). Следовательно, в точке, где Q III  0 , изгибающий момент имеет
экстремум. Найдём его. Из условия Q III  0 получаем:
Y
34
 YB  qz1  0 : z1  B 
 0,85 м.
q 40
Изгибающий момент при z1=0,85:
III
M max
 70  34  0,85  40  0,5  0,85 2  84,45 кН  м .
По этим данным строим эпюру поперечных сил (рис. 3, б) и
изгибающих моментов (рис. 3, в).
27
3. Подберём сечение балки. Наибольший изгибающий момент
(рисунок 3, в) равен 84,45 кН∙м. Необходимый момент сопротивления:
4.
Wх 
M max
 

84,45  103
155  10 6
 545  10  6 м3  545 см 3.
По таблицам сортамента [1] ближайшими к этому значению являются
Wх=518 cм3 (двутавр №30а) и Wх=597 cм3 (двутавр №33).
5. Проверим, годится ли двутавр №30а. Напряжения в нём будут
равны:
M x max 84,45  103


 163  10 6 Па  163 МПа.
Wx
518  10  6
Перенапряжение составляет:
% 
   
163  155
 100% 
 100%  5%,
 
155
что допустимо.
Таким образом, в соответствии с расчётом по нормальным
напряжениям следует принять двутавр №30а. Однако в сечении над левой
опорой балки действуют одновременно значительный изгибающий момент
М=80 кН∙м и большая поперечная (перерезывающая) сила Q=100 кН (рис. 3).
Поэтому в этом сечении надо сделать проверку по главным напряжениям.
6. Проверим условие прочности по третьей теории прочности. Из
таблиц сортамента выпишем для двутавра №30а: Iх=7780 см4; h=300 мм;
t=10,7 мм; d=6,5 мм.
Тогда в точке К сечения (рис. 4)
28
Рис. 4
Qbt
100  10 3  145  10  3  10,7  10  3
h  t  
300  10,7   10 3 Па  44,38 МПа;


3

8
2dI х
2  6,5  10  7780  10
M h 
80 10 3
   t 
(150  10,7) 10  3  143,2 10 6 Па  143,2МПа .
I х  2  7780 10 8
Согласно третьей теории прочности должно выполняться условие:
 2  4 2   .
В нашем случае:
 2  4 2  143,22  4  44,382  168,5  155МПа .
7. Определим перенапряжение в точке К.
Перенапряжение составляет:
168,5  155
% 
 100%  8,7%,
155
что недопустимо велико (более 5%).
Таким образом, надо использовать двутавр большего размера.
Окончательно принимаем двутавр №33.
29