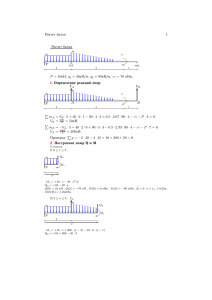
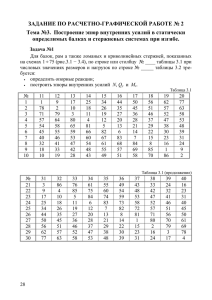
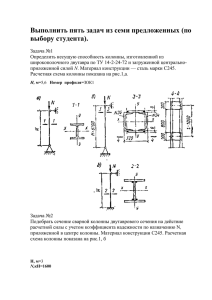
4.2. Подкрановая двухветвенная часть колонны Расчет производится для сечений III-III и IV-IV, т.е. на 8 сочетаний усилий: 1) М1 = 196,56 кНм 2) М2 = -53,98 кНм 3) М3 = 105,91 кНм 4) М4 = 69,65 кНм 5) М5 = 140,01 кНм 6) М6 = -238,80 кНм 7) М7 = -148,52 кНм 8) М8 = -36,01 кНм N1 = 1025,32 кН N2 = 537,72 кН N3 = 1136,46 кН N4 = 845,66 кН N5 = 1128,96 кН N6 = 735,22 кН N7 = 1240,10 кН N8 = 949,30 кН b1 = 1,0 b1 = 1,0 b1 = 1,0 b1 = 0.9 b1 = 1,0 b1 = 1,0 b1 = 1,0 b1 = 0.9 III-III IV-IV Из приведенных 8 сочетаний наиболее невыгодными являются №6 и №7, относящиеся к сечению IV, выбранному в месте заделки колонны в фундамент. Таким образом, все армирование подкрановой части колонны определяется расчетом прочности сечения IVIV. Геометрические характеристики подкрановой части колонны: 𝐻1 = 𝐻𝐻 = 10,8 м, h1 hн 1 м., b1 bk 0.5 м. Размеры сечения ветви: hc 0.25 м., bc b1 0.5 м., hc 0 0.25 0.04 0.21 м. Расстояние между осями ветвей: C h1 hc 1 0.25 0, 75 м. Количество панелей в соответствии с рисунком 2 n 4 . Среднее расстояние между осями распорок: 𝐻1 10,8 𝑆̅ = = = 2,7 м. 𝑛 4 а) для сочетаний усилий № 6. 𝑀6 238,8 = = 0,325 𝑁6 735,22 𝑙0 = 𝜓 ∙ 𝐻1 = 1,5 ∙ 10,8 = 16,2 м. 1.5 - т.к. в данном сочетании присутствует крановая нагрузка. Приведенный момент инерции сечения: 𝑒0 = 1 1 2 2 c2 0, 752 0.283 м. ired 2 2 3 0, 75 3 c 4 1 2 2 2 4 1 2 2 2 n hc 1.5 4 0.25 Приведенная гибкость: 𝑙 16,2 𝜆𝑟𝑒𝑑 = 0 = = 57,24 > 14 - в величине эксцентриситета необходимо учесть прогиб 𝑖𝑟𝑒𝑑 0,283 элемента. 2 2 b h3 0.5 0.253 c 0, 75 4 J1 2 c c bc hc 2 0.5 0.25 0.0364 м . 2 2 12 12 𝑀𝑙 = 𝑀пост + 𝑘1 ∙ 𝑀𝐶𝐻 + 𝑘2 ∙ 𝑀кр = −2,86 − 0,7 ∙ 8,77 − 0,5 ∙ 58,57 = −38,28 кНм; 𝑁𝑙 = 𝑁пост + 𝑘1 ∙ 𝑁𝐶𝐻 + 𝑘2 ∙ 𝑁кр = 530,23 + 0,7 ∙ 123,48 + 0,5 ∙ 104,29 = 668,81 кНм; 25 𝑐 0,75 = −38,28 − 668,81 ∙ = −289,08 кНм; 2 2 𝑐 0,75 𝑀61 = 𝑀6 ± 𝑁6 ∙ = −238,8 − 735,22 ∙ = −514,51 кНм; 2 2 𝑀6𝑙 289,08 𝜙𝑙 = 1 + 𝛽 = 1+1∙ = 1,56; 𝑀61 514,51 𝑒0 0,325 𝛿= = = 0,325 > 𝛿𝑚𝑖𝑛 = 0,15, ℎ2 1,0 принимаем 𝛿 = 0,325. Железобетонные колонны ОПЗ изготавливаются в горизонтальной опалубке. В процессе высвобождения из опалубки и транспортировки колонна работает как изгибаемый элемент, в растянутой зоне которого могут образовываться трещины. Чтобы гарантировать их отсутствие, продольная арматура должна быть не менее 16 диаметра. Зададимся предварительным процентом армирования: 2 As 2 6.03 0.0115 , bc hc 0 50 21 где As 6.03 см2 – площадь сечения арматуры, принятой в виде 3Ø16 А400. 𝑀6𝑙 = 𝑀𝑙 ± 𝑁𝑙 ∙ 2 0,852 c 0.000436 м4. Тогда I s 2 bc hc 0 2 0.0115 0.5 0.21 4 2 Критическая сила: 0,15 ∙ 𝐸𝑏 ∙ 𝐼 0,15 ∙ 30 ∙ 106 ∙ 0,000436 𝐷= + 0,7 ∙ 𝐸𝑠 ∙ 𝐼𝑠 = + 0,7 ∙ 20 ∙ 107 ∙ 0,000436 𝜙𝑙 ∙ (0,3 + 𝛿𝑒 ) 1,56 ∙ (0,3 + 0,325) = 0,63 ∙ 105 кН ∙ м2 𝑁𝑐𝑟 = 𝜋 2 ∙𝐷 𝑙02 = 3,142 ∙0,63∙105 16,22 = 2369 кН > 𝑁 = 735,22 кН - условие выполнено 1 = 1,45. 𝑁 735,22 1 − 𝑁6 1 − 2369 𝑐𝑟 Определяем усилия в ветвях колонны: поперечная сила в сечении IV – IV для сочетания №6 𝑄6 = 27,96 кН: 𝑁 𝑀 ∙𝜂 735,22 238,8∙1,45 𝑁𝑏1 = 26 + 6𝑐 = 2 + 0,75 = 436,98 кН - ветвь сжата; 𝜂= 𝑁6 𝑀6 ∙𝜂 735,22 1 = 238,8∙1,45 = 269,24 кН - ветвь сжата; 𝑄6 ∙ 𝑆̅ 27,96 ∙ 2,7 𝑀𝑏 = = = 18,87 кНм; 4 4 𝑀𝑏 18,87 𝑒0 = = = 0,043 м = 4,3 см. 𝑁𝑏1 436,98 Случайный эксцентриситет продольной силы ea принимается наибольшим из следующих значений: 𝑁𝑏2 = 2 − 𝑆̅ 𝑐 = 2 − 0,75 270 1. 𝑒𝑎 = 600 = 600 = 0,45 см; hc 25 0.83 см; 30 30 3. ea 1 см. 2. ea Поскольку эксцентриситет 4,3 см > ea ,max 1 см, в дальнейших расчетах используем его, ℎ −𝑎 0,25−0,04 тогда 𝑒 = 𝑒0 + 𝑐2 = 0,043 + = 0,148 м. 2 Окончательно, для сочетания усилий №6, на одну ветвь имеем: 𝑁𝑏1 = 436,98 кН; 𝑒 = 0,148 м. 26 б) для сочетания усилий №7. 𝑀7 148,52 = = 0,12; 𝑁7 1240,1 𝑙0 = 𝜓 ∙ 𝐻1 = 1,5 ∙ 10,8 = 16,2 м. 𝑙0 16,2 𝜆𝑟𝑒𝑑 = = = 57,24 > 14, 𝐼1 = 0,0364 м4 . 𝑖𝑟𝑒𝑑 0,283 𝑀𝑙 = 𝑀пост + 𝑘1 ∙ 𝑀𝐶𝐻 + 𝑘2 ∙ 𝑀кр = −2,86 − 0,5 ∙ 0,95 ∙ 8,77 − 0,5 ∙ 1 ∙ 54,03 = −34,04 кНм; 𝑁𝑙 = 𝑁пост + 𝑘1 ∙ 𝑁𝐶𝐻 + 𝑘2 ∙ 𝑁кр = 530,23 + 0,5 ∙ 0,95 ∙ 123,48 + 0,5 ∙ 1 ∙ 665,26 = 921,51 кНм; 𝑐 0,75 𝑀7𝑙 = 𝑀𝑙 ± 𝑁𝑙 ∙ = −34,04 − 921,51 ∙ = −379,61 кНм; 2 2 𝑐 0,75 𝑀71 = 𝑀7 ± 𝑁7 ∙ = −148,52 − 1240,0 ∙ = −613,56 кНм; 2 2 𝑀7𝑙 379,61 𝜙𝑙 = 1 + 𝛽 =1+1∙ = 1,619; 𝑀71 613,56 𝑒0 0,12 𝛿= = = 0,12 < 𝛿𝑚𝑖𝑛 = 0,15, ℎ2 1,0 принимаем 𝛿 = 0,15 I s 0.000436 см2 0,15 ∙ 𝐸𝑏 ∙ 𝐼 0,15 ∙ 30 ∙ 106 ∙ 0,000436 𝐷= + 0,7 ∙ 𝐸𝑠 ∙ 𝐼𝑠 = + 0,7 ∙ 20 ∙ 107 ∙ 0,000436 𝜙𝑙 ∙ (0,3 + 𝛿𝑒 ) 1,619 ∙ (0,3 + 0,15) = 0,64 ∙ 105 кН ∙ м2 𝑒0 = 𝑁𝑐𝑟 = 𝜋 2 ∙𝐷 𝑙02 = 3,142 ∙0,64∙105 16,22 = 2404 кН > 𝑁 = 1240,1 кН - условие выполнено 𝜂= Усилия в ветвях: 1 𝑁 1 − 𝑁7 𝑐𝑟 = 1 = 2,065. 1240,1 1 − 2404 𝑁7 𝑀7 ∙ 𝜂 1240,1 148,52 ∙ 2,065 + = + = 1028,98 кН 2 𝑐 2 0,75 𝑁7 𝑀7 ∙ 𝜂 1240,1 148,52 ∙ 2,065 𝑁𝑏2 = − = − = 211,12 кН 2 𝑐 2 0,75 𝑄7 ∙ 𝑆̅ 30,13 ∙ 2,7 𝑀𝑏 = = = 20,34 кНм; 4 4 𝑀𝑏 20,34 𝑒0 = = = 0,02 м = 2,0 см. 𝑁𝑏1 1028,98 ℎ𝑐 − 𝑎 0,25 − 0,04 𝑒 = 𝑒0 + = 0,02 + = 0,12 м. 2 2 Для сочетания усилий №7 имеем: 𝑁𝑏1 = 1028,98 кН; 𝑒 = 0,12 м. 𝑁𝑏1 = Сравнение основных параметров, при прочих равных условиях, определяющих необходимое для обеспечения прочности сечения колонны количество арматуры ( N b1 и e ), показывает, что в качестве наиболее неблагоприятного можно принять сочетание №7. Сочетание №7 27 𝑁𝑏1 1028,98 = = 0,676 𝛾𝑏1 ∙ 𝑅𝑏 ∙ 𝑏 ∙ ℎ𝑐0 1,0 ∙ 14,5 ∙ 1000 ∙ 0,5 ∙ 0,21 0,8 0,8 𝜉𝑅 = = = 0,533 < 𝛼𝑛 = 0,676 𝑅𝑠 350 1 + 700 1 + 700 𝛼 +𝜉 0,676+0,533 𝜉1 = 𝑛 2 𝑅 = = 0,605 < 1, т.е. дальнейший расчет выполняем при 𝜉1 = 0,605. 2 𝑀𝑏 + 𝑁𝑏1 ∙ (ℎ𝑐0 − 𝑎′ )/2 20,34 ∙ 105 + 1028980 ∙ (21 − 4)/2 𝛼𝑚1 = = = 0,337; 2 1 ∙ 14,5 ∙ 50 ∙ 212 ∙ 100 𝛾𝑏1 𝑅𝑏 𝑏ℎ𝑐0 a' 4 0.19 hс 0 21 𝛼𝑚1 − 𝜉1 (1 − 𝜉1 /2) 0,337 − 0,605 ∙ (1 − 0,605/2) 𝛼𝑠 = = = 0,105 1−𝛿 1 − 0,19 𝛼𝑛 (1 − 𝜉𝑅 ) + 2𝛼𝑠 𝜉𝑅 0,676 ∙ (1 − 0,533) + 2 ∙ 0,105 ∙ 0,533 𝜉= = = 0,632 1 − 𝜉𝑅 + 2𝛼𝑠 1 − 0,533 + 2 ∙ 0,105 𝜉 0,632 𝛾𝑏1 𝑅𝑏 𝑏ℎс0 𝛼𝑚1 − 𝜉 (1 − 2) 1,0 ∙ 14,5 ∙ 50 ∙ 21 0,337 − 0,632 ∙ (1 − 2 ) 𝐴𝑠 = 𝐴′𝑠 = ∙ = ∙ 𝑅𝑠 1−𝛿 350 1 − 0,19 = 5,12 см2 2 ∙ 𝐴𝑠 2 ∙ 5,12 𝜇= = = 0,01 < 𝜇 = 0,0115. 𝑏𝑠 ∙ ℎ𝑐0 50 ∙ 21 Так как процент армирования получился меньше, чем принятый ранее из условия трещиностойкости, то перерасчет не делаем. Принимаем 316 А400 с Аs = 6,03 см2. Поперечная арматура принята 6 А240 (из условия сварки) с шагом 200 мм, что меньше 15d = 1516 = 240 мм и не более 500 мм. 𝛼𝑛 = Расчет колонны из плоскости поперечной рамы Проверим необходимость расчета подкрановой части колонны перпендикулярной к плоскости поперечной рамы: 0,8 - при наличии вертикальных связей между колоннами 𝑙0 = 𝜓 ∙ 𝐻1 = 0,8 ∙ 10,8 = 8,64 м. b2 502 i 1 14, 43 см; 12 12 𝑙′0 864 𝜆′ = = = 59,88. 𝑖′ 14,43 Т.к. ’ = 59,88 > red = 53 расчет из плоскости рамы необходим. в плоскости, Проведем расчет из плоскости рамы для сочетания 7. М7‘= 0 кНм N7 = 1240,1 кН Nl = 921,51 кН. 𝐻1 1080 𝑒𝑎 = = = 1,8 > 1 см 600 600 Так как расчет производится из плоскости рамы, то изменяются функции рассматриваемого сечения IV-IV. b = 0.5м – высота сечения; 2hc = 0.5м – ширина сечения. h0б 0.5 0.04 0.46 м. ℎоб − 𝑎′ 0,46 − 0,04 𝑀′7𝑙 = 0 ± 𝑁𝑙 ∙ (𝑒𝑎 + ) = 0 + 921,51 ∙ (0,018 + ) = 210,1 кНм; 2 2 28 ℎоб − 𝑎′ 0,46 − 0,04 𝑀′7𝑙 = 0 ± 𝑁7 ∙ (𝑒𝑎 + ) = 0 + 1240,1 ∙ (0,018 + ) = 228,74 кНм; 2 2 𝑀′7𝑙 210,1 𝜙𝑙 = 1 + 𝛽 = 1+1∙ = 1,92; 𝑀′71 228,74 𝑒𝑎 0,018 𝛿= = = 0,036, 𝑏1 0,5 min 0,15 ; т.к. < min, принимаем = 0.15; 𝐼𝑠 = 2 ∙ ̅̅̅ 𝐴𝑠 ∙ (0,5 ∙ 𝑏1 − 𝑎′ ) = 2 ∙ (4 ∙ 2,01) ∙ 10−4 ∙ (0,5 ∙ 0,5 − 0,04) = 0,000071 м4 h b 3 0.25 0.53 I 2 c c 2 0.00521 12 12 Критическая сила: 0,15 ∙ 𝐸𝑏 ∙ 𝐼 0,15 ∙ 30 ∙ 106 ∙ 0,00521 𝐷= + 0,7 ∙ 𝐸𝑠 ∙ 𝐼𝑠 = + 0,7 ∙ 20 ∙ 107 ∙ 0,000071 𝜙𝑙 ∙ (0,3 + 𝛿𝑒 ) 1,92 ∙ (0,3 + 0,15) = 0,371 ∙ 105 кН ∙ м2 𝑁𝑐𝑟 = 𝜋 2 ∙𝐷 𝑙02 = 3,142 ∙0,371∙105 8,64 2 = 4897 кН > 𝑁 = 1240,1 кН - условие выполнено 𝜂= 1 𝑁 1 − 𝑁7 𝑐𝑟 = 1 = 1,339. 1240,1 1 − 4897 ℎоб − 𝑎 0,46 − 0,04 𝑒′ = 𝜂𝑒𝑎 + = 1,339 ∙ 0,018 + = 0,234 м. 2 2 𝑁7 1240,1 ∙ 1000 𝛼𝑛 = = = 0,572 > 𝜉𝑅 = 0,533 𝛾𝑏1 ∙ 𝑅𝑏 ∙ 2ℎ𝑐 ∙ ℎоб 1,0 ∙ 14,5 ∙ 100 ∙ 50 ∙ 46 𝛼𝑛 + 𝜉𝑅 0,572 + 0,533 𝜉1 = = = 0,553 < 1 2 2 𝑁7 ∙ 𝑒′ 1240,1 ∙ 1000 ∙ 23,4 𝛼𝑚1 = = = 0,189; 2 1 ∙ 14,5 ∙ 50 ∙ 462 ∙ 100 𝛾𝑏1 𝑅𝑏 ∙ 2ℎ𝑐 ∙ ℎоб a' 4 0.087 h0 б 46 𝛼𝑚1 − 𝜉1 (1 − 𝜉1 /2) 0,189 − 0,553 ∙ (1 − 0,553/2) 𝛼𝑠 = = < 0. 1−𝛿 1 − 0,087 Арматура по расчету не требуется. Оставляем принятую арматуру из расчета в плоскости рамы 316 А400 с Аs = 6,03 см2. 4.3. Промежуточная распорка. Максимальная поперечная сила, действующая в сечениях подкрановой части колонны Q = 30,13 кН. Изгибающий момент в распорке: 𝑄 ∙ 𝑆̅ 30,13 ∙ 2,7 𝑀𝑑𝑠 = = = 40,68 кНм; 2 2 Поперечная сила в распорке: 2 ∙ 𝑀𝑑𝑠 2 ∙ 40,68 𝑄𝑑𝑠 = = = 108,47 кНм. 𝑐 0,75 Размеры сечения распорки: b b1 0.5 м, h 0.4 м, h0 h a 0.4 0.04 0.36 м. 29 Площадь продольной рабочей арматуры при симметричном армировании: 𝑀𝑑𝑠 40,68 ∙ 105 𝐴𝑠 = 𝐴′𝑠 = = = 3,63 см2 . 𝑅𝑠 ∙ (ℎ0 − 𝑎′ ) 350 ∙ 100 ∙ (36 − 4) Принимаем 3Ø16 А400 с As 6,03 см2 > 3,63 см2. Поперечная сила, воспринимаемая бетоном, b 2 b1 Rbt b h0 2 но не более 2,5 b1 Rbt b h0 и не менее 0,5 b1 Rbt b h0 Qb с b 2 1,5 c – величина проекции опасной наклонной трещины на продольную ось распорки, принимаемой равной 2h0, но не более расстояния в свету между внутренними гранями ветвей, т.е. (hн - 2hс) В нашем случае 2h0 2 0,36 0,72 (hн 2hc ) (1 2 0.25) 0.5 Принимаем c = 0.5м 𝑄𝑏 = 1,5∙1,0∙1,05∙1000∙0,5∙0,362 0,5 = 102,06 кН, что больше 0,5 b1 Rbt b h0 = 0,5 ∙ 1,0 ∙ 1,05 ∙ 1000 ∙ 0,5 ∙ 0,36 = 94,5 кН и не превышает 2,5 b1 Rbt b h0 = 2,5 ∙ 1,0 ∙ 1,05 ∙ 1000 ∙ 0,5 ∙ 0,36 = 472,5 кН. 𝑄𝑏 = 102,06 кН < 𝑄𝑑𝑠 = 108,47 кН , поэтому расчет поперечной арматуры необходим из условия: Q Qb Qsw Qsw sw qsw c Диаметр поперечной арматуры назначаем из условия сварки с продольной: Ø6 А400; Аsw 0,126см 2 , количество каркасов 2, Rsw 285МПа Проекция опасной наклонной трещины на продольную ось распорки c=0.5м. Максимально допустимый шаг поперечных стержней: 𝛾𝑏1 𝑅𝑏 𝑏ℎ02 1,0 ∙ 1,05 ∙ 50 ∙ 362 𝑠𝑚𝑎𝑥 = = = 62,7 см 𝑄𝑑𝑠 108,47 Требуемый шаг поперечных стержней по длине распорки: 𝜑 ∙𝑅 ∙𝐴 ∙𝑛∙𝑐 0,75∙285∙0,126∙2∙50 𝑠𝑠𝑤 = 𝑠𝑤 𝑄 𝑠𝑤−𝑄𝑠𝑤 = (108,47−102,06)∙10 = 42,02, что не превышает 𝑠𝑚𝑎𝑥 = 62,7 см. 𝑑𝑠 𝑏 Конструктивные требования: шаг из условия: S w 3 h0 270 мм 500 мм 4 Принимаем шаг поперечных стержней 50 мм. Проверим соблюдение требований принятого шага по интенсивности поперечного армирования по длине распорки 𝑅𝑠𝑤 ∙ 𝐴𝑠𝑤 ∙ 𝑛 285 ∙ 0,126 ∙ 2 ∙ 10 𝑞𝑠𝑤 = = = 143,64 кН/м > 0,25𝛾𝑏1 𝑅𝑏𝑡 𝑏 𝑠𝑠𝑤 5 = 0,25 ∙ 1 ∙ 1,05 ∙ 50 ∙ 10 = 131,25 см Поскольку условие выполняется, окончательно принимаем поперечную арматуру в виде Ø6 А400 с шагом 50. 30 V. РАСЧЕТ ФУНДАМЕНТА ПОД КРАЙНЮЮ КОЛОННУ Грунты основания – однородные. Преобладающий компонент – суглинки. Удельный вес грунта = 20 кН/м3. Условное расчетное сопротивление грунта R0 = 0,21 МПа. Усилия, передающееся с колонны на фундамент, соответствуют сочетанию №7 для сечения IV-IV. Для этого сочетания имеем: М = 148,52 кНм, N = 1240,1 кН, Q = -30,13 кН. Материалы фундамента. Бетон класса В15: – расчетное сопротивление осевому сжатию Rb = 8,5 МПа – расчетное сопротивление осевому растяжению Rbt = 0,75 МПа – начальный модуль упругости Eb = 24103 МПа Арматура класса А400: – расчетное сопротивление растяжению/сжатию I г.п.с. Rs = Rsс = 350 МПа – начальный модуль упругости Es = 2105 МПа Расчетная нагрузка от веса нижней стеновой панели и остекления на участке между отметками +2,0 м и +11,0 м: 𝐺𝑤3 = (2,5 ∙ 2,0 + 0,4 ∙ 9) ∙ 6 ∙ 1,1 ∙ 1 = 56,76 кН Расчетная нагрузка от собственного веса фундаментной балки: GФБ GСВБ f n 29 1.1 1 31,9кН Где, GСВБ 29кН собственный вес фундаментной балки при шаге колонн 6 м. Указанные нагрузки передаются на фундамент с эксцентриситетом: 1 1 e4 w h1 0,3 1 0,65 2 2 Тогда, расчетное значение момента от данных нагрузок будет равно: 𝑀Б.𝑊 = (𝐺𝑤3 + 𝐺ФБ ) ∙ 𝑒4 = (56,76 + 31,9) ∙ 0,65 = 57,63 кНм Окончательно для расчета имеем: М = 148,52 – 57,63 = 90,89 кНм N = 1240,1 + 56,76 + 31,9 = 1328,76 кН Q = 30,13 кН Диаметр продольной арматуры в подкрановой части колонны d = 16 мм. Высота фундамента определяется из условий: - обеспечения заделки колонны в фундаменте для двухветвенной колонны в плоскости поперечной рамы: H ф , з hз 0.25 м; hз 0.5 0.33 h1 0.5 0.33 1 0,83 0,85 м; hз 1.5 b1 1.5 0.5 0.75 м; Тогда: H ф, з hз 0, 25 м 0.85 0.25 1.1 м. - обеспечения анкеровки рабочей арматуры колонны: H ф, ан hан 0,25 м ; где 0,25м – минимальная толщина дна стакана (0,2м) с учетом доливки под колонну (0,05м) R A h0, an s s Rbond U s где As и Us – соответственно площадь поперечного сечения анкеруемого стержня арматуры и периметр его сечения ( в нашем случае для арматуры 16 As= 2,011 см2; 𝑈𝑠 = 𝜋𝑑 = 3,14 ∙ 1,6 = 5,02 см); 31 Rbond 1 2 Rbt 2,5 1 0,75 1,875 МПа – расчётное сопротивление сцепления арматуры с бетоном, принимаемое равномерно распределённым по длине анкеровки; 1 – коэффициент, учитывающий влияние вида поверхности арматуры (для горячекатаной арматуры периодического профиля 1=2,5); 2 – коэффициент, учитывающий влияние размера диаметра арматуры (для продольной арматуры диаметром 16 мм 2=1). 350 ∙ 2,011 ℎ0,𝑎𝑛 = = 74,78 см. 1,875 ∙ 5,02 Требуемая расчётная длина анкеровки арматуры с учётом конструктивного решения элемента в зоне анкеровки определяется по формуле: 𝐴𝑠,𝑐𝑎𝑙 3,63 ℎ𝑎𝑛 = 𝛼 ∙ ℎ0,𝑎𝑛 ∙ = 0,75 ∙ 74,78 ∙ = 33,76 см, 𝐴𝑠,𝑒𝑓 6,03 где As,cal и As,ef – площади поперечного сечения арматуры, соответственно требуемая по расчёту и фактически установленная (так как рабочая арматура по расчету не требуется, то As,cal=0 – коэффициент, учитывающий влияние на длину анкеровки напряжённого состояния бетона и арматуры (для сжатых стержней периодического профиля =0,75). Кроме того, согласно СП 52-101-2003 “Бетонные и железобетонные конструкции без предварительного напряжения арматуры”, фактическую длину анкеровки необходимо принимать ℎ𝑎𝑛 ≥ 0,3ℎ0,𝑎𝑛 = 0,3 ∙ 74,78 = 22,43 см ℎ𝑎𝑛 ≥ 15𝑑𝑠 = 15 ∙ 1,6 = 24 см han 20 см. Принимаем han 70см , тогда H ф, ан 0,7 0, 25 0,95 м H ф, з 1.1м Расчетная глубина промерзания равна d f 0.7 0.23 78,4 1.42 H ф, з 1.1м . Где, d0=0.23 – для песков средней крупности; Mt=78,4; kh=0.7. Глубина заложения фундамента должна быть не менее df. Принимаем высоту фундамента Н = 1,3 м (кратно 50 мм), что больше Нз = 1,1 м и Нан = 0,95 м. Глубина заложения при этом составит d H ф a1 1.3 0.15 1.45 м d f 1.42 м Размеры подошвы фундамента. Площадь подошвы: Nn A 1,1 R0 d где 1,05 – коэффициент, учитывающий наличие изгибающего момента; 𝑁 1240,1 𝑁𝑛 = = = 1078 кН 𝛾𝑓 1,15 Получим: 1078 А = 1,1 ∙ = 6,55 м2 0,21 ∙ 1000 − 20 ∙ 1,45 Зададимся соотношением большей стороны подошвы к меньшей: l / b = 1,2. Тогда 𝐴 6,55 𝑏 = √1,2 = √ 1,2 = 2,34 м; 𝑙 = 1,2𝑏 = 1,2 ∙ 2,34 = 2,81 м. 32 Принимаем lb = 3,32.7 м (кратно 0,3 м). Уточняем площадь подошвы: A l b 3,3 2,7 8,91 м2. Момент сопротивления: b l 2 2,7 3,32 W 4,9 м3. 6 6 Уточняем нормативное давление на грунт: k b b0 d d 0 , R R0 1 1 b0 2d 0 где k1= 0,005 – для суглинков; b0 = 1 м; d0 = 2 м. 0.005 (2,7 1) 1.45 2 R 0.21 1 2 2 0.183МПа . 1 Уточняем размеры подошвы: 1078 А = 1,1 ∙ = 7,75 м2 0,182 ∙ 1000 − 20 ∙ 1,45 𝐴 7,75 𝑏 = √1,2 = √ 1,2 = 2,54 м; 𝑙 = 1,2𝑏 = 1,2 ∙ 2,54 = 3,05 м. Принимаем lb = 3,63,0 м. Уточняем площадь подошвы: A l b 3,6 3 10,8 м2. Момент сопротивления: b l 2 3,0 3,62 W 6,48 м3. 6 6 Уточняем нормативное давление на грунт: k b b0 d d 0 , R R0 1 1 b0 2d 0 где k1= 0,005 – для суглинков; b0 = 1 м; d0 = 2 м. 0.005 (3,0 1) 1.45 2 R 0.21 1 2 2 0.183МПа . 1 Уточняем размеры подошвы: 1078 А = 1,1 ∙ = 7,7 м2 0,183 ∙ 1000 − 20 ∙ 1,45 𝐴 7,7 𝑏 = √1,2 = √1,2 = 2,53 м; 𝑙 = 1,2𝑏 = 1,2 ∙ 2,53 = 3,04 м. Принимаем lb = 3,63,0 м. Оставляемый принятый до этого фундамент. Размеры фундамента. Высота фундамента Н = 1,3 м. lи.с. 1.6 м, bи.с. 1.1 м , что на 0,6 м больше соответствующих размеров поперечного сечения подкрановой части колонны. Толщина стенки стакана по верху dh = 0,2 м. Вынос подошвы фундамента за грань стакана: 33 l lи .с. 3,6 1.6 1 м > 0,45 м, 2 2 поэтому устраиваем вторую ступень: h f 2 0.3 Высота стакана hи.с. H h f 1,3 0.3 2 0.7 м. Глубина стакана hh = 1,05 м Толщина дна стакана min 0,2 м. hbot H hh 1.3 1,05 0.25 м > hbot c2 Расчет прочности элементов фундамента. Определение краевых ординат эпюры давления от нормативных нагрузок. Момент в уровне подошвы: 90,89 30,13 𝑀𝑛,𝑓 = 𝑀𝑛 + 𝑄𝑛 𝐻𝑓 = + ∙ 1,3 = 136,81 кНм. 1,15 1,15 Нормативная нагрузка от веса фундамента и грунта на его обрезках: Gn l b d n 3,6 3 1.45 20 1 313,2 кН. l 3,6 𝑀𝑛,𝑓 136,81 0.6 м – эпюра напряжений в грунте 𝑒0 = 𝑁 +𝐺 = 1078+313,2 = 0,098 м < 𝑛 𝑛 6 6 трапецивидная. 𝑁 +𝐺 6𝑒 1078+313,2 6∙0,098 𝑃𝑛,𝑚𝑎𝑥 = 𝑛𝐴 𝑛 ∙ (1 + 𝑙 0) = ∙ (1 + ) = 154,06 кН/м2 < 10,8 3 < 1,2R = 1,2183 = 219,6 кН/м2, 1078 + 313,2 6 ∙ 0,098 𝑃𝑛,𝑚𝑖𝑛 = ∙ (1 − ) = 103,57 кН/м2 > 0. 10,8 3 Расчет арматуры подошвы фундамента а) в плоскости поперечной рамы 𝑁 𝑀𝑓 1078 136,81 ∙ 1,15 𝑃𝑚𝑎𝑥 = + = + = 124,09 кН/м2 𝐴 𝑊 10,8 6,48 𝑁 𝑀𝑓 1078 136,81 ∙ 1,15 𝑃𝑚𝑖𝑛 = − = − = 75,54 кН/м2 𝐴 𝑊 10,8 6,48 Сечение I-I. 𝑃𝑚𝑎𝑥 − 𝑃𝑚𝑖𝑛 124,09 − 75,54 ∙ 𝑐1 = 124,09 − ∙ 0,5 = 117,35 кН/м2 𝑙 3,6 (2𝑃𝑚𝑎𝑥 + 𝑃𝐼−𝐼 ) ∙ 𝑏 ∙ 𝑐12 (2 ∙ 124,09 + 117,35) ∙ 3 ∙ 0,52 𝑀𝐼−𝐼 = = = 45,69 кНм 6 6 Рабочая высота подошвы h01 h f a 0.3 0.05 0.25 м = 25 см. Площадь арматуры 𝑀𝐼−𝐼 45,69 ∙ 105 𝐴𝑠1 = = = 5,8 см2 𝑅𝑠 ∙ 0,9 ∙ ℎ01 350 ∙ 102 ∙ 0,9 ∙ 25 𝑃𝐼−𝐼 = 𝑃𝑚𝑎𝑥 − Сечение II-II. 𝑃𝐼𝐼−𝐼𝐼 = 𝑃𝑚𝑎𝑥 − 𝑃𝑚𝑎𝑥 − 𝑃𝑚𝑖𝑛 124,09 − 75,54 ∙ 𝑐2 = 124,09 − ∙ 1 = 110,6 кН/м2 𝑙 3,6 34 𝑀𝐼𝐼−𝐼𝐼 (2𝑃𝑚𝑎𝑥 + 𝑃𝐼𝐼−𝐼𝐼 ) ∙ 𝑏 ∙ 𝑐22 (2 ∙ 124,09 + 110,6) ∙ 3 ∙ 12 = = = 179,39 кНм 6 6 Рабочая высота подошвы h02 H a 0,6 0.05 0,55 м = 55 см. Площадь арматуры 𝑀𝐼𝐼−𝐼𝐼 179,39 ∙ 105 𝐴𝑠2 = = = 10,35 см2 𝑅𝑠 ∙ 0,9 ∙ ℎ02 350 ∙ 102 ∙ 0,9 ∙ 55 Сечение III-III. 𝑃𝑚𝑎𝑥 − 𝑃𝑚𝑖𝑛 𝑙 − ℎ1 124,09 − 75,54 3,6 − 1 ∙ = 124,09 − ∙ 𝑙 2 3,6 2 = 106,56 кН/м2 𝑙 − ℎ1 2 3,6 − 1 2 (2𝑃𝑚𝑎𝑥 + 𝑃𝐼𝐼𝐼−𝐼𝐼𝐼 ) ∙ 𝑏 ∙ ( 2 ) (2 ∙ 124,09 + 110,6) ∙ 3 ∙ ( 2 ) = = 6 6 = 299,76 кНм 𝑃𝐼𝐼𝐼−𝐼𝐼𝐼 = 𝑃𝑚𝑎𝑥 − 𝑀𝐼𝐼𝐼−𝐼𝐼𝐼 Рабочая высота подошвы h03 H a 1,3 0.05 1,25 м = 125 см. Площадь арматуры 𝑀𝐼𝐼𝐼−𝐼𝐼𝐼 299,76 ∙ 105 𝐴𝑠3 = = = 7,61 см2 𝑅𝑠 ∙ 0,9 ∙ ℎ03 350 ∙ 102 ∙ 0,9 ∙ 125 Проведем подбор арматуры. Из двух найденных Asi принимаем As,max = As2 = 14,89 см2. Зададимся шагом стержней S = 200 мм. Расстояние от края подошвы до первого стержня примем as = 50 мм. Количество стержней: l 2 as 3 2 0.05 n2 1 1 15,5 - нецелое число. S 0.2 Примем крайний шаг 200мм, а остальные 250мм. l 2 as 3 2 0.05 2 0, 2 n2 2 1 1 11 n2 13 S 0.25 В направлении короткой стороны подошвы имеем арматуру 1314 А400 с As = 20,07 см2. Процент армирования в сечениях: As 20,07 100% 100% 0.267% ; I-I: 1 b h01 300 25 As 20,07 II-II: 1 100% 100% 0.122% ; (300 2 0,475) 55 b 2сb1 h02 As 20,07 100% 100% 0.145% . III-III: 2 bи .с. h03 110 125 Поскольку во всех сечениях max = 1% > > min = 0,1%, количество принятой арматуры не изменяем. Принимаем: 1314 А400 с As = 20,07 см2. б) из плоскости поперечной рамы 35 Сечение V-V. 𝑃𝑚𝑎𝑥 + 𝑃𝑚𝑖𝑛 124,09 + 75,54 = = 99,82 кН/м2 2 2 2 𝑏−𝑏 3,0 − 1,1 2 𝑃𝐼𝑉−𝐼𝑉 ∙ 𝑙 ∙ ( 2 и.с. ) 99,82 ∙ 3,6 ∙ ( ) 2 = = = 162,15 кНм 2 2 𝑃𝐼𝑉−𝐼𝑉 = 𝑀𝐼𝑉−𝐼𝑉 Рабочая высота подошвы h01 h f a 0.6 0.05 0.55 м = 25 см. Площадь арматуры 𝑀𝐼𝑉−𝐼𝑉 162,15 ∙ 105 𝐴𝑠3 = = = 9,36 см2 𝑅𝑠 ∙ 0,9 ∙ ℎ01 350 ∙ 102 ∙ 0,9 ∙ 55 Зададимся шагом стержней S = 250 мм. Расстояние от края подошвы до первого стержня примем as = 50 мм. Количество стержней: l 2 as 3,6 2 0.05 n2 1 1 15 - целое число. S 0.25 В направлении длинной стороны подошвы имеем арматуру 1514 А400 с As = 23,09 см2. Процент армирования в сечении: As 23,09 V-V: 5 100% 100% 0,161% min 0,1% . (360 100)55 l c2 h02 As 23,09 100% 100% 0, 256% min 0,1% . l h01 360 25 As 23,09 100% 100% 0,115% min 0,1% . IV-IV: 6 luc h03 160 125 Принимаем: 1514 А400 с As = 23,09 см2. IV-VI: 4 Армирование стакана фундамента Площадь арматуры продольной арматуры определяют из расчета стенок стакана на внецентренное сжатие нормального сечения А-А. В данном курсовом примем площадь продольной арматуры без расчета, исходя из минимального % армирования. min 0,1% As min Ab 0.001 (luc buc aст bст ) 0,001(160 110 110 60) 11см 2 Принимаем 616 А400 с As = 12,07 см2. Поперечное армирование принимаем в виде горизонтальных сеток, с заведением из за ближайшую к стакану ступень (но не менее 5-ти сеток, шаг сеток 150мм), с расположением стержней у наружной и внутренней поверхности стенок стакана. Принимаем арматуру сеток по конструктивным соображениям из стержней 10А240. 36 37