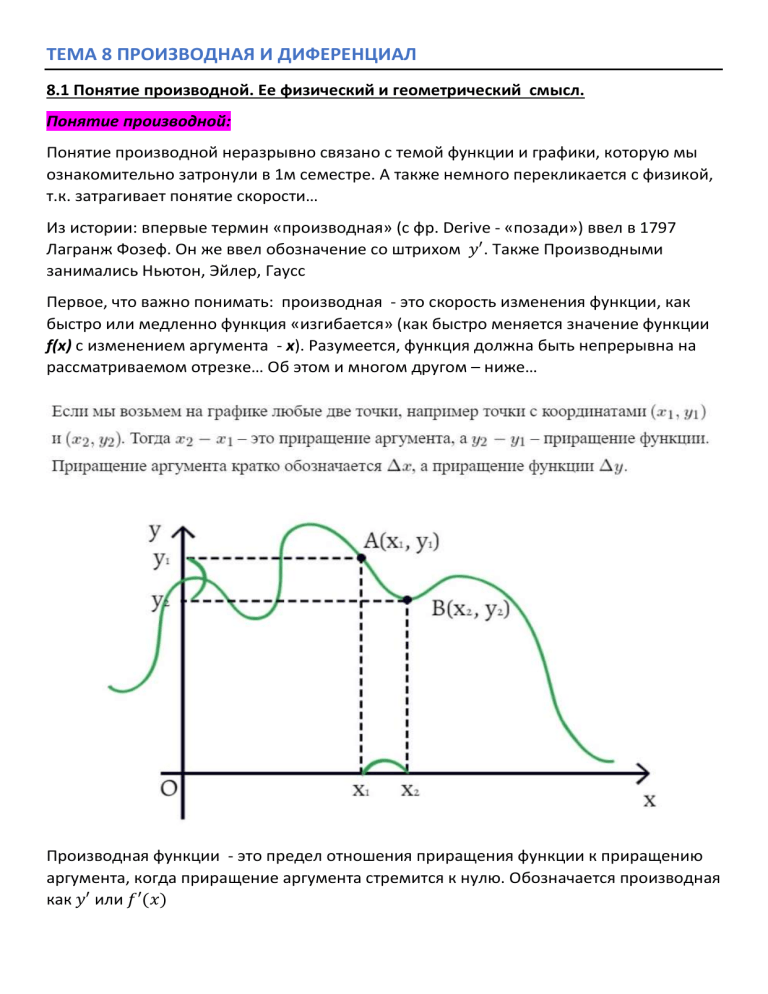
ТЕМА 8 ПРОИЗВОДНАЯ И ДИФЕРЕНЦИАЛ 8.1 Понятие производной. Ее физический и геометрический смысл. Понятие производной: Понятие производной неразрывно связано с темой функции и графики, которую мы ознакомительно затронули в 1м семестре. А также немного перекликается с физикой, т.к. затрагивает понятие скорости… Из истории: впервые термин «производная» (с фр. Derive - «позади») ввел в 1797 Лагранж Фозеф. Он же ввел обозначение со штрихом 𝑦′. Также Производными занимались Ньютон, Эйлер, Гаусс Первое, что важно понимать: производная - это скорость изменения функции, как быстро или медленно функция «изгибается» (как быстро меняется значение функции f(x) с изменением аргумента - x). Разумеется, функция должна быть непрерывна на рассматриваемом отрезке… Об этом и многом другом – ниже… Производная функции - это предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Обозначается производная как 𝑦′ или 𝑓′(𝑥) 𝑦 = lim ∆ → ∆𝑦 ∆𝑥 Т.е. рассматривается т.В, которая по графику сокращает расстояние до т.А, за счет того, что 𝑥 → 𝑥 (стремясь с ней слиться). Или, если так будет понятнее, воображаемый прямоугольный треугольник, со сторонами: ∆𝑥 = 𝑥 − 𝑥 и ∆𝑦 = 𝑦 − 𝑦 с достаточно видимого теперь начнет «сдуваться» пока не станет бесконечно малым у самой точки А. Геометрический смысл производной: Только по нашему рисунку есть замечание и знакомый вам момент из темы графики: У нас красная секущая, которая стремится стать касательной, убывает, а значит в ее уравнении (ур.прямой) угловой коэффициент будет отрицательным: 𝒚 = −𝒌𝒙 + 𝒃. А по нашей новой теме, мы уже знаем, что этот самый угловой коэффициент как раз и есть производная и в нашем конкретном случае имеем c ростом Х – падение Y (главная функция тоже убывает): ∆𝒚 = 𝒚𝟏 − 𝒚𝟐 , а значит ∆𝒚 < 𝟎. И этот минус подтянется и в ответ при расчете производной. Вот и отрицательный результат 𝑦 < 0 ⟹ 𝑡𝑔 𝛼 < 0. Требования к существованию производной: Производная существует (имеет вполне нормальное значение) не для всех подряд функций. Существуют четкие требования: А) Функция должна быть задана и непрерывна на рассматриваемом участке Б) Тот самый предел lim ∆ ∆ → ∆ существует и конечен. А вот если предела нет, то это, обычно, связано с тем, что в исследуемой точке как нельзя провести касательную к данной функции или же она будет под 90 градусов к оси ОХ (а вы помните из темы тригонометрия, что тангенса нет в 90град). В Этом случае 𝑦 = ∞ Примеры решалок по поиск приращения функции: Задание 1. Найти приращение ∆𝑦 для функции 𝑦 = 𝑥 , если 𝑥 = 2,5 𝑥 = 2 Решение: здесь все просто: находим значения функции 𝑦 = 𝑓(𝑥) и 𝑦 = 𝑓(𝑥 ) и потом остается найти из полученных значений ∆𝒚 = 𝒚 − 𝒚𝟎 𝑦 = 𝑓(𝑥) = 2,5 = 6,25 и 𝑦 = 𝑓(𝑥 ) = 2 = 4 ∆𝒚 = 𝑦 − 𝑦 = 6,25 − 4 = 𝟐, 𝟐𝟓 Или можно было записывать решение одной строкой: ∆𝒚 = 𝑦 − 𝑦 = 2,5 − 2 = 6,25 − 4 = 𝟐, 𝟐𝟓 Ответ: ∆𝒚 = 2,25 Задание 2 . Дана функция 𝑦 = . Найти приращение ∆𝑦 , если 𝑥 = 1 и ∆𝑥 = 0,2 Решение: пример очень похож на предыдущий. Для поиска ∆𝑦 необходимо найти значения функции 𝑦 = 𝑓(𝑥) и 𝑦 = 𝑓(𝑥 ) и потом ∆𝒚 = 𝒚 − 𝒚𝟎 1)Но сначала найдем 𝑥 = 𝑥 + ∆𝑥: 𝑥 = 1 + 0,2 = 1,2 2) 𝑦 = 𝑓(𝑥 ) = = 1 и 𝑦 = 𝑓(𝑥) = , = 0,83 3) ∆𝑦 = 𝑦 − 𝑦 = 0,83 − 1 = −0,17 Ответ: ∆𝒚 = −0,17 Физический смысл производной: Как мы говорили в начале статьи, производная – это скорость изменения функции. Вот как раз о скорости, как о физической составляющей производной и поговорим…. Если взглянуть на произвольный график скорости, то мы увидим функциональную зависимость S от t. (где как раз и видны более и менее скоростные участки графика) И изучаемая нами производная измеряет именно мгновенную скорость в конкретный момент времени. В нашем случае все рассматривается так: Есть т.наз. средняя скорость, найденная как отношение пройдённого отрезка дистанции ∆𝑆 за определенный интервал времени ∆𝑡: 𝑉ср = ∆𝑆 ∆𝑡 А мгновенная скорость – это скорость, измеренная за бесконечно малый промежуток времени ∆𝑡 → 0, как некий предел средней скорости в данной точке 𝑡 А этот механизм и рассчитывается производной: 𝑉мгн = lim перемещение показывают вектором) ∆ ∆ → ∆ (векторная величина, т.к. Мгновенную скорость изображают как вектор в данной точке (как раз та самая касательная к графику) Решать задачки на мгновенную скорость мы будем в следующем материале 8.2. И, как видите, тема очень интересная. Она затрагивает и функции и физику, является неотъемлемой частью почти всех вычислений высшей математики…







