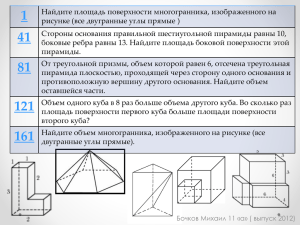
4*5=20 «********» 1*4=4 S=(17+16+20+4)

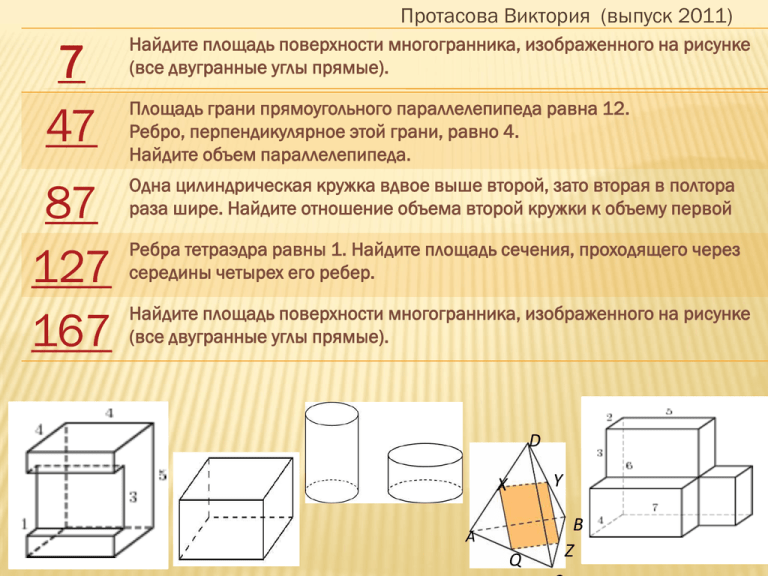
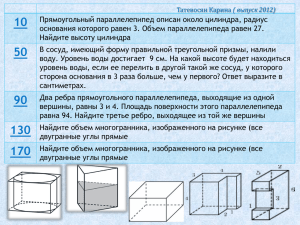
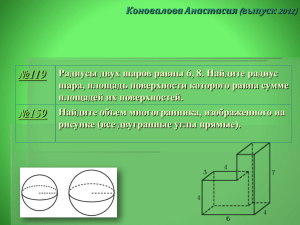
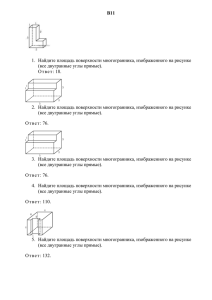
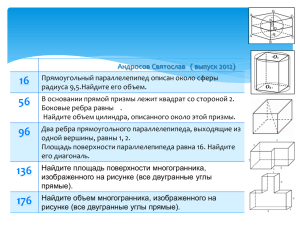
Протасова Виктория (выпуск 2011)
7
47
87
127
167
Найдите площадь поверхности многогранника, изображенного на рисунке
(все двугранные углы прямые).
Площадь грани прямоугольного параллелепипеда равна 12.
Ребро, перпендикулярное этой грани, равно 4.
Найдите объем параллелепипеда.
Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора
раза шире. Найдите отношение объема второй кружки к объему первой
Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через
середины четырех его ребер.
Найдите площадь поверхности многогранника, изображенного на рисунке
(все двугранные углы прямые).
D
Y
X
А
Q
B
Z
№7.( № 25661)
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
Ответ: S=114
ЛЕВАЯ-ПРАВАЯ:
4*5 – 1*3 = 17
ВЕРХНЯЯ –НИЖНЯЯ:
4*4 = 16
ЗАДНЯЯ-ПЕРЕДНЯЯ:
4*5=20
«ЗАПЛАТКИ»
1*4=4
S=(17+16+20+4)*2=114
№47(№ 27076)
ПЛОЩАДЬ ГРАНИ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА РАВНА 12.
РЕБРО, ПЕРПЕНДИКУЛЯРНОЕ ЭТОЙ ГРАНИ, РАВНО 4.
НАЙДИТЕ ОБЪЕМ ПАРАЛЛЕЛЕПИПЕДА.

V=Sосн * H =12*4=48

Ответ:V=48
№87(№ 27118)
ОДНА ЦИЛИНДРИЧЕСКАЯ КРУЖКА ВДВОЕ ВЫШЕ ВТОРОЙ, ЗАТО ВТОРАЯ В ПОЛТОРА
РАЗА ШИРЕ. НАЙДИТЕ ОТНОШЕНИЕ ОБЪЕМА ВТОРОЙ КРУЖКИ К ОБЪЕМУ ПЕРВОЙ.
№127(№ 27175)
РЕБРА ТЕТРАЭДРА РАВНЫ 1. НАЙДИТЕ ПЛОЩАДЬ СЕЧЕНИЯ, ПРОХОДЯЩЕГО ЧЕРЕЗ
СЕРЕДИНЫ ЧЕТЫРЕХ ЕГО РЕБЕР.
XYZQ-параллелограмм,
D
так как вершинами являются середины сторон пространственного
четырехугольника
Y
X
при этом УХ I УZ и УХ = УZ
так как УХǁAB , УХ=0,5AB и YZǁCD, YZ=0,5CD ,
B
а AB I CD , AB=CD по свойству правильного тетраэдра
А
Z
Q
=>XYZQ-квадрат ; S= 1/2 * 1/2 =0,25
С
Ответ: S=0,25
№167(№ 77156)
НАЙДИТЕ ПЛОЩАДЬ ПОВЕРХНОСТИ МНОГОГРАННИКА, ИЗОБРАЖЕННОГО НА
РИСУНКЕ (ВСЕ ДВУГРАННЫЕ УГЛЫ ПРЯМЫЕ).
2 способ
Площади поверхностей параллелепипедов
Прямоугольники «соприкосновения»
(5*3+2*3)*2=42
S=(104+62+32)-42=198-42=156
1 способ
Передняя-задняя
6*7-3*2 = 36
Левая-правая
6*4-2*3=18
Верхняя-нижняя
4*7-2*2=24
S=(36+18+24)*2=156