16 - yarkovskayaschool.ru

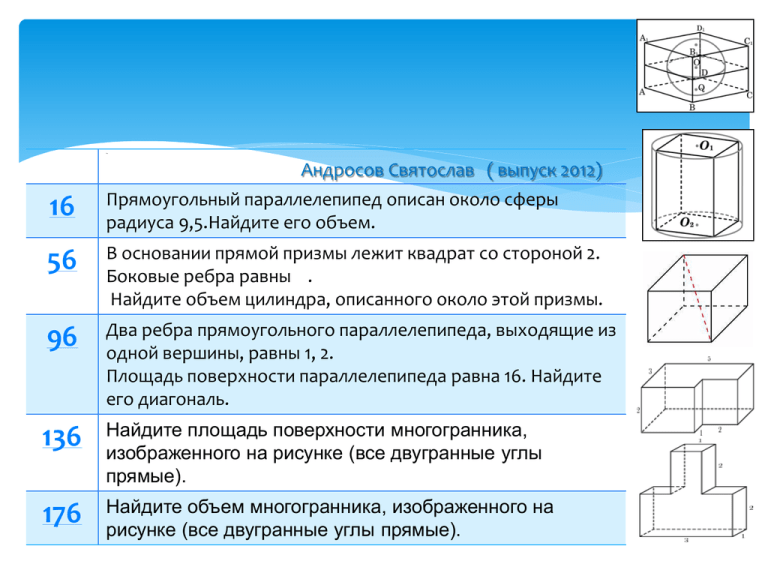
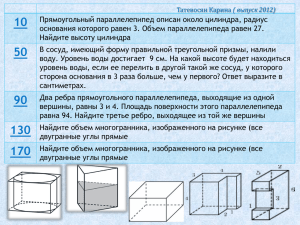
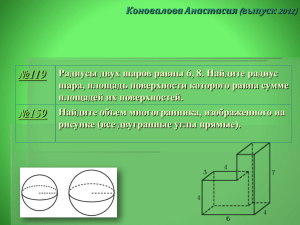
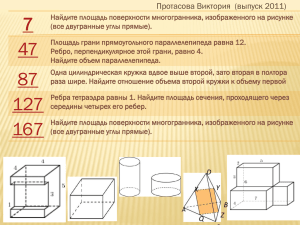
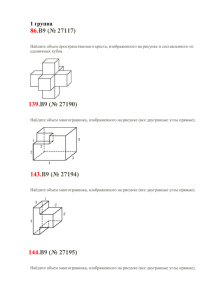
Анд
Андросов Святослав ( выпуск 2012)
16
Прямоугольный параллелепипед описан около сферы
радиуса 9,5.Найдите его объем.
56
В основании прямой призмы лежит квадрат со стороной 2.
Боковые ребра равны .
Найдите объем цилиндра, описанного около этой призмы.
96
Два ребра прямоугольного параллелепипеда, выходящие из
одной вершины, равны 1, 2.
Площадь поверхности параллелепипеда равна 16. Найдите
его диагональ.
136
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы
прямые).
176
Найдите объем многогранника, изображенного на
рисунке (все двугранные углы прямые).
Прямоугольный параллелепипед описан 4891
около сферы радиуса 9,5.
Найдите его объем.
Решение:
Ребро куба равно диаметру
вписанного в него шара,
а объем куба равен кубу его ребра.
Vk=(𝟗, 𝟓 + 𝟗, 𝟓)𝟑
Vk=6859
Ответ: 6859
В основании прямой призмы лежит квадрат со стороной 2.
Боковые ребра равны .
Найдите объем цилиндра, описанного около этой призмы.
Решение:
Диагональ квадрата в основании
призмы
𝒅=𝒂 𝟐=𝟐 𝟐
является диаметром описанного
вокруг призмы цилиндра.
Тогда его объем:
𝝅𝒅𝟐
V=H
𝟒
=
Ответ: 4
𝟐 𝝅(𝟐 𝟐)𝟐
( )
=4
𝝅
𝟒
Два ребра прямоугольного параллелепипеда,
выходящие из одной вершины, равны 1, 2.
Площадь поверхности параллелепипеда равна 16.
Найдите его диагональ.
S= 2(a·b + b·c +c·a)
16= 2(1·2 + 2·c +c·1)
8= 2+ 3·c ;
c=2
𝒅=
𝒂𝟐 + 𝒃𝟐 + 𝒄𝟐
𝒅=
𝟏𝟐 + 𝟐𝟐 + 𝟐𝟐 = 𝟑
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
Площадь поверхности заданного многогранника
равна:
3*5-1*2=13 (верхняя и нижняя грань)
2*3=6
(левая и правая грань)
2*5=10
(передняя и задняя грань)
S=(13+6+10)*2=58
Найдите объем многогранника,
изображенного на рисунке
(все двугранные углы прямые).
Решение:
Объем данного многогранника
равен сумме объемов
параллелепипедов со
сторонами 1,1,2 и 1,2,3:
V=V1+V2=2+6=8