Геометрическая вероятность. Урок 3
реклама

Урок 3
Геометрическая
вероятность.
Геометрическая модель.
Многие практические задачи приводят к
вопросам теории вероятности, которые не
укладываются в разобранную выше схему конечного
числа попарно несовместных исходов испытаний.
Пусть, например, стержень наудачу разламывается на
три части. Какова вероятность того, что из
получившихся отрезков можно будет построить
треугольник?
В этой задаче мы имеем бесконечное множество
исходов, так как разлом может попасть на любую точку
стержня. Здесь мы будем пользоваться иным
определением вероятности, которое назовем
геометрическим.
A
C
D
B
Рассмотрим следующую модель. Пусть на
отрезок АВ бросают наудачу точку. Назовем
вероятностью попадания этой точки на часть этого
отрезка отношение длины этой части к длине всего
отрезка ( если часть состоит из нескольких кусков,
то надо сложить длины этих кусков). Вместо
отрезка АВ можно взять некоторую
геометрическую фигуру, имеющую конечную
площадь и считать вероятностью попасть в часть X
этой фигуры отношение площадей указанной части
и всей фигуры.
Итак, геометрическая вероятность – это
вероятность попадания точки в некоторую область.
(отрезок, часть плоскости, шар, и т.д.)
Пусть Ω – область на плоскости, DΩ. μ(Ω),
μ(D) – площади этих областей.
В Ω наудачу бросается случайная точка ω.
Вероятность попадания в любую подобласть
области Ω зависит только от её площади. Тогда
P{ωD} = μ(D) / μ(Ω).
Замечание.
Геометрическая модель имеет ограниченную
область применения ввиду требования равновозможности
отдельных точек.
Пример 1. Вернемся к задаче о разламывании стержня.
Пусть на отрезок длины 1 бросают наудачу две точки. Они
разбивают отрезок на три отрезка. Какова вероятность,
что из полученных трех отрезков можно сложить
треугольник?
Заданный отрезок рассматриваем как отрезок [0,1]
числовой прямой. Тогда наудачу брошенные точки имеют
координаты – числа x и y, принадлежащие отрезку [0,1].
0
x
y
1
Но любую пару чисел можно
рассматривать как координаты точки на
плоскости. Поскольку 0≤x≤1, 0≤y≤1, то эти точки
(x,y) наудачу брошены в квадрат со стороной 1.
Посмотрим теперь какую фигуру образуют
точки, координаты которых удовлетворяют
условию примера.
Для того, чтобы из этих трех отрезков
можно было построить треугольник, необходимо
и достаточно, чтобы длины этих отрезков
удовлетворяли неравенству треугольника.
При x≤y получаем: x<(y-x)+(1-y);
y-x<x+(1-y);
1-y<x+(y-x),
что после преобразований дает систему
неравенств:
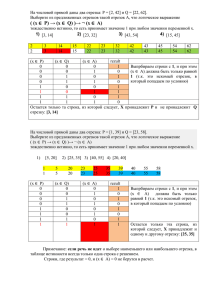
x 0, 5,
Y
y x 0, 5,
y 0, 5,
x y,
B
1
C
A
0,5
X
0,5
1
которой на плоскости XOY
соответствует треугольник
ABC, площадь которого S=1/8.
При x > y получаем: y < (x-y) +(1-x);
x-y < y +(1-x);
1-x < y +(x-y),
что после преобразований дает систему неравенств:
y 0, 5,
y x 0, 5,
x 0, 5,
x y,
Y
1
N
0,
5
M
K
0,5
1
X
которой на плоскости XOY
соответствует треугольник NMK
площадь которого S=1/8.
Площадь квадрата равна 1. Следовательно,
вероятность построить треугольник равна
P=(1/8+1/8)/1=1/4.
Пример 2. (задача Бюффона) . На плоскости
проведено семейство параллельных прямых.
Расстояние между соседними прямыми равно m.
На эту плоскость наудачу бросается отрезок
длины m. Какова вероятность, что отрезок
пересекается хоть с одной прямой из этого
семейства?
Решение.
x
y
B
A
Рис. 1
Y
y=m sinx
m
Рис.2
π
Обозначим через y расстояние от верхнего конца отрезка
до ближайшей снизу прямой. Проведем луч с началом в
верхней (левой) точке отрезка, параллельный прямым
семейства и идущий направо. Обозначим через x угол
между этим лучом и отрезком. Мы получили пару чисел,
удовлетворяющих неравенствам: 0≤x<π, 0≤y≤m. Точка
(x,y) с такими координатами наудачу брошена в
прямоугольник (рис2).
X
Для того, чтобы отрезок пересекался хотя
бы с одной из прямых семейства, необходимо и
достаточно выполнение неравенства
y ≤ |AB| = m sinx ,
которым на рисунке 2 определена заштрихованная
фигура. Найдем ее площадь:
S1 m sin x dx m cos x 0 2m.
0
Так как площадь прямоугольника, в
который наудачу брошена точка, S=πm, то
искомая в примере вероятность
p=S1/S=2m/πm=2/π.
Пример 3. (задача о встрече). Два школьника
условились встретиться в определенном месте между
12 и 13 часами дня. Пришедший первым ждет второго
в течении ¼ часа, после чего уходит. Какова
вероятность, что встреча состоится, если каждый
студент наудачу выбирает момент своего прихода?
Решение.
0 ≤ x ≤ 1, 0 ≤ y ≤ 1, |y-x| ≤ 1/4.
Y
Тогда
1
y ≤ x +1/4, y ≥ x - 1/4.
Sкв.=1, Sф=1-2(3/4·3/4·1/2)=
1/4
1/4
1
X
1-9/16 = =7/16.
Следовательно, p=Sф/Sкв.=7/16.