Документ 411066

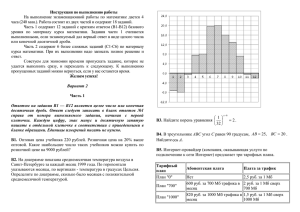
ГАУ ДПО (ПК) С «Брянский областной центр оценки качества образования»
Демонстрационный вариант теста в 20102011 учебном году, предлагаемый для
прохождения аттестации на вторую, первую
и высшую категории
Математика
г. Брянск
Инструкция по выполнению работы
На выполнение экзаменационной работы по математике дается 4 часа (240 мин).
Работа состоит из двух частей и содержит 18 заданий.
Часть 1 содержит 12 заданий с кратким ответом (В1-В12) базового уровня по
материалу курса математики. Задания части 1 считаются выполненными, если экзаменуемый
дал верный ответ в виде целого числа или конечной десятичной дроби.
Часть 2 содержит 6 более сложных заданий (С1-С6) по материалу курса математики.
При их выполнении надо записать полное решение и ответ.
Советуем для экономии времени пропускать задание, которое не удается выполнить
сразу, и переходить к следующему. К выполнению пропущенных заданий можно вернуться,
если у вас останется время.
В1-В12 оцениваются по 1 баллу
С1-С2 оцениваются по 2 балла
С3-С4 оцениваются по 3 балла
С5-С6-оцениваются по 4 балла
Максимальное количество баллов-30
Часть 1
Ответом на задания B1-B12 должно быть целое число или конечная десятичная дробь.
Ответ следует записать в бланк ответов № 1 справа от номера выполняемого задания,
начиная с первой клеточки. Каждую цифру, знак минус и запятую пишите в отдельной
клеточке в соответствии с приведенными в бланке образцами. Единицы измерений
писать не нужно.
B1
B2
Цена одной шоколадки в супермаркете 20 рублей, но в воскресенье действует
специальное предложение: заплатив за 2 шоколадки, покупатель получает 3 таких
шоколадки (одну бесплатно). Какое наибольшее количество шоколадок можно
получить в воскресенье, имея 380 рублей?
На рисунке жирными точками показано суточное количество осадков,
выпадавших в Архангельске с 5 по 14 ноября 1964 года. По горизонтали
указываются числа месяца, по вертикали - количество осадков, выпавших в
соответствующий день, в миллиметрах. Для наглядности жирные точки на
рисунке соединены линией. Определите по рисунку, сколько дней из данного
периода выпадало более 3 миллиметров осадков.
B3
B4
Найдите
корень
уравнения,
или
сумму
корней,
если
их
несколько
значений
функции
x 2  x  6   x 2  3x  18 .
Найти
сумму
наибольшего
и
y  144 sin 2 x  16 cos 2 x .
наименьшего
B5
Интернет-провайдер (компания, оказывающая услуги по подключению к сети
Интернет) предлагает три тарифных плана.
Тарифный план
Абонентская плата
Плата за трафик
1. План «0»
2. План «700»
Нет
900 рублей за 700 Мб трафика
в месяц
1300 рублей за 1000 Мб
трафика в месяц
4 рубля за 1 Мб
3,5 рубля за 1 Мб сверх 700 Мб
3. План «1000»
3 рубля за 1 Мб сверх 1000 Мб
Пользователь планирует, что его трафик составит 800 Мб и исходя из этого
выбирает наиболее дешевый тарифный план. Сколько рублей заплатит
пользователь за месяц, если его трафик действительно будет равен 800 Мб?
Какова масса пробкового шара диаметром 2м в тоннах? Плотность пробки 0,25 г
B6
/см
3
(ответ округлите до целых).
Найдите значение выражения:
B7
B8
2 log 3 8  log 2 3  2 log6 7  3log6 7
На рисунке изображены график функции y = f (x) и касательная к этому графику,
проведенная в точке с абсциссой x0. Найдите значение производной функции f (x)
в точке x0.
B9
B10
В цилиндрическом сосуде уровень жидкости достигает 80 см. На какой высоте
будет находиться уровень жидкости, если ее перелить во второй цилиндрический
сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в
сантиметрах.
Для одного из предприятий-монополистов зависимость объема спроса на
продукцию q (единиц в месяц) от ее цены p (тыс. руб.) задается формулой: q = 70
- 5p. Определите максимальный уровень цены p (в тыс. руб.), при котором
значение выручки предприятия за месяц
руб.
B11
B12
r  q p
составит не менее 240 тыс.
Найдите точку максимума функции
y  ( x 2  12 x  12)e5 x
Первая труба пропускает на 3 литра воды в минуту меньше, чем вторая труба.
Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом
130 литров она заполняет на 3 минуты быстрее, чем первая труба?
Часть 2
Для записи решений и ответов на задания C1-C6 используйте бланк ответов № 2.
Запишите сначала номер выполняемого задания, а затем полное обоснованное решение и
ответ.
С1
Найдите корни уравнения
определения функции
С2
С3
sin 2 2 x  2 cos 2 x,
принадлежащие области
y  sin x cos x .
В правильной треугольной призме ABCA1B1C1 известны ребра: AB= 3 3 . BB1 =
6. Точка M - середина ребра B1C1, а точка T - середина A1M. Найдите угол между
плоскостью BCT и прямой AT.
Решите неравенство
log 2 ( x 2  7 x  10)

log 5x6 ( x 2  9)
log 2 ( x 2  9)
log 5x6 10
С4
Две окружности, касающиеся прямой в точках A и B, пересекаются в точках C и
D, причем AB=12, CD=5. Найти медиану CE треугольника ABC.
С5
Найдите все значения a, при каждом из которых наименьшее значение функции f
(x)=- x2 + 7| x - a | - x на отрезке [-5; 5] принимается хотя бы на одном из концов
этого отрезка.
С6
Найдите все пары натуральных чисел a и b, удовлетворяющие равенству
ba  a b  20
(в левой части стоит число, получаемое дописыванием
десятичной записи числа a после десятичной записи числа b).