Инструкция по выполнению работы

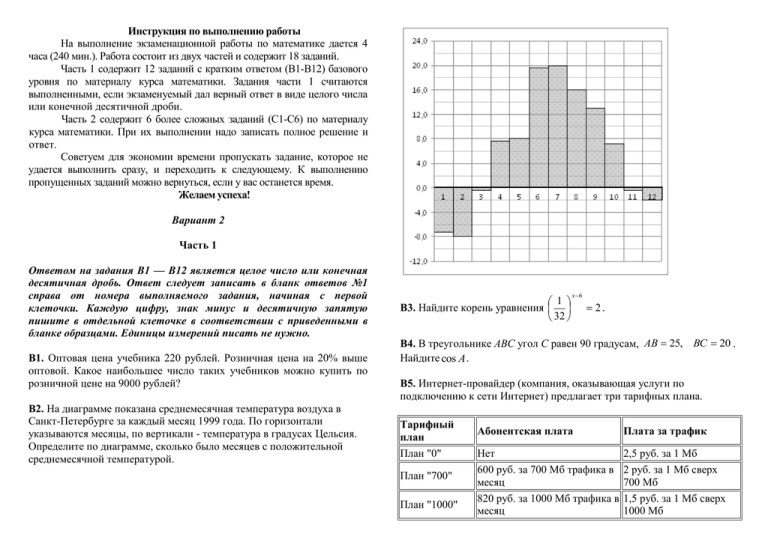
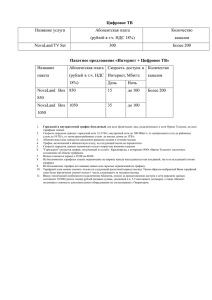
Инструкция по выполнению работы
На выполнение экзаменационной работы по математике дается 4
часа (240 мин.). Работа состоит из двух частей и содержит 18 заданий.
Часть 1 содержит 12 заданий с кратким ответом (В1-В12) базового
уровня по материалу курса математики. Задания части 1 считаются
выполненными, если экзаменуемый дал верный ответ в виде целого числа
или конечной десятичной дроби.
Часть 2 содержит 6 более сложных заданий (С1-С6) по материалу
курса математики. При их выполнении надо записать полное решение и
ответ.
Советуем для экономии времени пропускать задание, которое не
удается выполнить сразу, и переходить к следующему. К выполнению
пропущенных заданий можно вернуться, если у вас останется время.
Желаем успеха!
Вариант 2
Часть 1
Ответом на задания В1 — В12 является целое число или конечная
десятичная дробь. Ответ следует записать в бланк ответов №1
справа от номера выполняемого задания, начиная с первой
клеточки. Каждую цифру, знак минус и десятичную запятую
пишите в отдельной клеточке в соответствии с приведенными в
бланке образцами. Единицы измерений писать не нужно.
В1. Оптовая цена учебника 220 рублей. Розничная цена на 20% выше
оптовой. Какое наибольшее число таких учебников можно купить по
розничной цене на 9000 рублей?
В2. На диаграмме показана среднемесячная температура воздуха в
Санкт-Петербурге за каждый месяц 1999 года. По горизонтали
указываются месяцы, по вертикали - температура в градусах Цельсия.
Определите по диаграмме, сколько было месяцев с положительной
среднемесячной температурой.
 1 
В3. Найдите корень уравнения  
 32 
x 6
 2.
В4. В треугольнике ABC угол C равен 90 градусам, АВ  25, ВС  20 .
Найдите cos A .
В5. Интернет-провайдер (компания, оказывающая услуги по
подключению к сети Интернет) предлагает три тарифных плана.
Тарифный
план
План "0"
План "700"
План "1000"
Абонентская плата
Плата за трафик
Нет
600 руб. за 700 Мб трафика в
месяц
820 руб. за 1000 Мб трафика в
месяц
2,5 руб. за 1 Мб
2 руб. за 1 Мб сверх
700 Мб
1,5 руб. за 1 Мб сверх
1000 Мб
Пользователь предполагает, что его трафик составит 750 Мб в месяц и,
исходя из этого, выбирает наиболее дешевый тарифный план. Сколько
рублей заплатит пользователь за месяц, если его трафик действительно
будет равен 750 Мб?
Определите скорость велосипедиста, если известно, что он прибыл в
пункт В на 6 часов позже автомобилиста. Ответ дайте в км/ч.
В6. На клетчатой бумаге с клетками размером 1 см 1 см изображен
треугольник (см. рисунок). Найдите его площадь в квадратных
сантиметрах.
Для записи решений и ответов на задания С1 ― С6 используйте
бланк ответов № 2. Запишите сначала номер выполняемого
задания, а затем полное обоснованное решение и ответ.
Часть 2
tgx
 4  tgx
2

2
3 0





С1. Решите систему уравнений:  9 
;
3

 6 y  2 cos x  0
х 2
2 х
 5 х  1 при х  3
х
х
В8. Материальная точка движется прямолинейно по закону
x(t )  t 2  13t  23 (где x — расстояние от точки отсчета в метрах, t —
время в секундах, измеренное с начала движения). В какой момент
времени (в секундах) ее скорость была равна 3 м/с?
В9. Основанием прямой призмы является прямоугольный треугольник
4
с катетами 10 и 7. Боковые ребра равны . Найдите объем цилиндра,

описанного около этой призмы.
В10. Для одного из предприятий-монополистов зависимость объема
спроса на продукцию q (единиц в месяц) от цены p (тыс. руб.) задается
формулой: q=80-5p. Определите максимальный уровень цены p ( в тыс.
руб.), при котором значение выручки предприятия за месяц r=q∙p
составит не менее 315 тысяч рублей.
B11. Найдите наибольшее значение функции y  4 x  2tgx    9 на
 
отрезке 0;  .
 3
В12. Из пункта А в пункт В, расстояние между которыми 75 км,
одновременно выехали автомобилист и велосипедист. Известно, что за
час автомобилист проезжает на 40 км больше, чем велосипедист.
В7. Найдите значение выражения

C2. В правильной треугольной призме ABCA1B1C1 известны
ребра: АВ  6 3 , ВВ1  5 . Точка М – середина ребра В1С1, а точка Т –
середина А1М. Найдите угол между плоскостью ВСТ и прямой АТ.
С3. Решите неравенство:
log 7 x 8 18
log 5 x 2  9 x  18
;

log 7 x 8 x 2  16
log 5 x 2  16






С4. Две окружности, касающиеся прямой в точках А и В,
пересекаются в точках С и D, причем, АВ=28, СD=45. Найдите медиану
СЕ треугольника АВС.
5. Найдите все значения а при каждом из которых наименьшее
значение функции
f x    x 2  9 x  a  x на отрезке  9; 8
принимается хотя бы на одном из концов этого отрезка.
С6. Найдите все пары натуральных чисел а и в,
удовлетворяющие равенству ва  а в  90 (в левой части стоит число,
получаемое дописыванием десятичной записи числа а после
десятичной записи числа в).