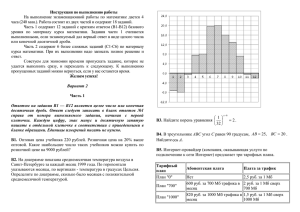
Свойства функции y=tg x
реклама

Государственной учреждение образования «Средняя школа № 12г.Гомеля» Функции y=tgx и y=ctgx их свойства и графики Свойства функции y=tg x 1.Область определения функции y=tgx-множество действительных чисел х ≠π/2+ πn, n ∈ Z. 2.Множество значений функции y=tgx – все действительные числа, т.е. множество R. 3.Функция y=tgx периодическая с периодом π. 4.Наибольшего и наименьшего значений функция y=tgx не имеет. 5.График функии проходит через точку(0;0)- на число координат; с осью Oy он пересекаетя только в точке(0;0),а с осью Ox- в точках(πn;0) n ∈ Z. 6. Нулями функции y=tgx являются значения аргумента x= πn, n ∈ Z. 7. Функция y=tgx принимает отрицательные значения на каждом из промежутков (- π/2+ πn; πn), n ∈ Z. 8. Функция y=tgx нечетная. 9. Функция y=tgx возрастает на каждом из промежутков (- π/2+ πn; π/2+ πn), n ∈ Z. свойствах функции y=ctgx 1.Область определения функции y=ctgxмножество действительных чисел х ≠πk, k ∈ Z. 2.Множество значений y=ctgx-все действительные числа,т.е. множество R. 3. Функция y=сtgx периодическая с периодом π. 4.Наибольшего и наименьшего значений функция y=сtgx не имеет. 5.График функии не имеет общих точек с осью Оу, а с осью Ох пересекается в точках(π/2+ πk; 0),k ∈ Z. 6.Нулями функции y=сtgx являются значения аргумента x= π/2 + πk, k ∈ Z. 7. Функция y=ctgx принимает отрицательные значения на каждом из промежутков (π/2+ πk; π+ πk), k ∈ Z. 8. Функция y=ctgx нечетная. 9. Функция y=ctgx убывает на каждом из промежутков (πk; π+ πk), k ∈ Z.