l 1
реклама

Задачи 1 тура отраслевой олимпиады по физике
9 класс
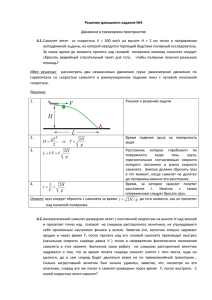
1. На дне сосуда с жидкостью укреплена шарнирно тонкая
деревянная палочка длиной 41 см, часть которой длиной 12 см
выступает над поверхностью жидкости. Найти отношение
плотности жидкости к плотности дерева.
𝑙
𝑙1
2
2
Решение: Из условия равновесия палочки: 𝑚𝑔 cos 𝛼 = 𝐹𝐴
cos 𝛼 , где l – длина
палочки, l1 – длина ее затопленной части. Отсюда 𝑚𝑔𝑙 = 𝐹𝐴 𝑙1 , 𝜌д 𝑆𝑙𝑔𝑙 = 𝜌ж 𝑔𝑆𝑙1 𝑙1 ,
𝜌д 𝑙2 = 𝜌ж 𝑙12 ,
𝜌ж
𝜌д
𝑙 2
= ( ) ≈ 2.
𝑙1
2. Период малых колебаний математического маятника возрастает в n = 1,05 раза в
ускоряющемся самолете. Самолет двигается по прямой с ускорением a = 0,23g. Под
каким углом к горизонту двигается самолет?
𝑙
𝑙
𝑔
𝑔`
Решение: 𝑇 = 2𝜋√ , 𝑇` = 2𝜋√
𝑚𝑔` =
𝑚𝑔
𝑛2
𝑛=
,
𝑇
𝑇`
=√
𝑔
𝑔`
, 𝑔` =
𝑔
𝑛2
. Сила натяжения 𝐹н =
. С другой стороны, 𝑚𝑎⃗ = 𝐹⃗н + 𝑚𝑔⃗ , отсюда 𝐹н2 = (𝑚𝑎)2 + (𝑚𝑔)2 −
π
𝑚2 (𝑎2 +𝑔2 )−𝐹н2
2
2𝑚2 𝑎𝑔
2𝑚𝑎𝑚𝑔 cos β, где β = − α, а α – искомый угол. cos β = sin α =
=
0,5. Значит, α = π/6.
3. В электрическом чайнике находится вода, имеющая температуру 22 °С,
удельную теплоемкость 4,2 кДж/(кг∙К) и удельную теплоту парообразования 2,3
МДж/кг. После включения чайника вода в нем закипела через 5 минут и
испарилась полностью еще через некоторое время. Найти это время.
Решение: 𝑃𝑡1 = 𝑐𝑚∆𝑇, 𝑃𝑡2 = 𝜆𝑚,
𝑡2
𝑡1
=
𝜆
𝑐Δ𝑇
, 𝑡2 =
𝜆𝑡1
𝑐Δ𝑇
= 35,1 мин.
4. Два резистора, сопротивление которых отличается в α = 4,8 раза, включают в
цепь постоянного тока при неизменном напряжении в цепи один раз
последовательно, а другой – параллельно. Каково отношение N2/N1 тепловых
мощностей, выделяющихся на резисторах во втором N2 и в первом N1 случаях?
Решение: 𝑅1 = 𝑅 + 𝛼𝑅, 𝑅2 =
𝑅𝛼𝑅
𝑅+𝛼𝑅
, 𝑁1 =
𝑈2
𝑅(𝛼+1)
, 𝑁2 =
𝑈 2 (𝛼+1)
𝛼𝑅
,
𝑁2
𝑁1
=
(𝛼+1)2
𝛼
≈ 7.
10 класс
1. Круглая горизонтальная платформа вращается вокруг своей оси с частотой 18
мин-1. В направлении к центру платформы со скоростью 7 м/c скользит шайба.
Найти скорость шайбы относительно платформы в момент, когда расстояние до
центра составляет 6 м.
Решение: 𝜔 = 2𝜋𝜈, 𝑣∥ = 𝜔𝑅 = 2𝜋𝜈𝑅. 𝑣 = √𝑣∥2 + 𝑣⊥2 =13,3 м/c.
2. Задана система двух частиц массами m1 = 5 кг и m2 = 3 кг, имеющих скорости
𝑣
⃗⃗⃗⃗=
3 𝑒⃗⃗⃗⃗𝑥 −2 ⃗⃗⃗⃗⃗
𝑒𝑦 + 𝑒⃗⃗⃗⃗𝑧 и ⃗⃗⃗⃗⃗=𝑒
𝑣2 ⃗⃗⃗⃗𝑥 +4 𝑒⃗⃗⃗⃗⃗𝑦 −6 ⃗⃗⃗⃗
𝑒𝑧 (м/с). Найти суммарный импульс частиц
1
после их столкновения и разлета.
Решение: 𝑝⃗ = ⃗⃗⃗⃗
𝑝1 + ⃗⃗⃗⃗⃗
𝑝2 = ⃗⃗⃗⃗⃗⃗
𝑝10 + ⃗⃗⃗⃗⃗⃗⃗
𝑝20 = 𝑚1 ⃗⃗⃗⃗
𝑣1 + 𝑚2 ⃗⃗⃗⃗⃗
𝑣2 =
(18 𝑒⃗⃗⃗⃗𝑥 +2 ⃗⃗⃗⃗⃗
15 𝑒⃗⃗⃗⃗𝑥 −10 𝑒⃗⃗⃗⃗⃗𝑦 +5 ⃗⃗⃗⃗
𝑒𝑧 +3 𝑒⃗⃗⃗⃗𝑥 +12 ⃗⃗⃗⃗⃗
𝑒𝑦 −18 𝑒⃗⃗⃗⃗=
𝑒𝑦 −13 𝑒⃗⃗⃗⃗)кг
∙ м/с.
𝑧
𝑧
3. Один моль идеального одноатомного газа совершает процесс
1231, при котором температура
T2 = 2T1, а отношение
количеств тепла, полученных газом, Q12/Q23 = 1,08. Найти
количество тепла, полученное газом в ходе цикла, если T1 = 100
К.
3
𝑄12
2
1,08
Решение: 𝑄12 = 𝜈𝑅Δ𝑇12 , 𝑄23 =
5
53
3
32
, 𝑄31 = Δ𝑈31 =
5
𝜈𝑅Δ𝑇21 = − 𝜈𝑅Δ𝑇12 ,
2
Δ𝑇12 = 𝑇2 − 𝑇1 = 𝑇1 , 𝑄 = 𝑄12 + 𝑄23 + 𝑄31 = 324,09 Дж.
4. Центр уединенной проводящей сферы радиуса R = 0,1 м
совпадает с началом координат, внутри и вне сферы – вакуум.
Координаты точечных зарядов Q = 4∙10-5 Кл и q = 5∙10-7 Кл
соответственно {0; 0,05} м
и {0,2; 0} м. Найти силу,
действующую на заряд q, если постоянная закона Кулона k =
9∙109 Н∙м2/Кл2.
Решение: геометрия задачи позволяет пренебречь отклонением заряда Q центра.
Поэтому 𝐹 =
𝑘𝑞𝑄
𝑟2
= 4,5 Н.
11 класс
1. Брусок находится на горизонтальной доске, с коэффициентом трения µ, которая
двигается в горизонтальном направлении по закону x = a∙sinωt, где х –
горизонтальная координата доски в момент времени t, a и ω – положительные
постоянные. При каком условии во время движения брусок не будет
проскальзывать по доске?
Решение: 𝑚𝑎макс < 𝐹тр = 𝜇𝑚𝑔 , 𝑎макс = 𝑎𝜔2 . Поэтому должно быть 𝑎𝜔2 < 𝜇𝑔.
2. Два автомобиля с двигателями мощностью N1 и N2 развивают скорости v1 и v2.
Какую скорость они развивают, если их сцепить буксировочным тросом?
Решение: 𝑁1 = 𝐹1 𝑣1 , 𝑁2 = 𝐹2 𝑣2 , 𝑁1 +𝑁2 = (𝐹1 +𝐹2 )𝑣 = (
𝑁1
𝑣1
+
𝑁2
𝑣2
)𝑣 .
3. В двух теплоизолированных баллонах объемом V1 и V2, соединенных трубкой с
краном, находится один и тот же идеальный газ при одинаковых давлениях, но
разных температурах T1 и T2. Какая температура установится в баллонах, если кран
открыть?
Решение: 𝑃(𝑉1 +𝑉2 ) = (𝜈1 +𝜈2 )𝑅𝑇 , 𝑃(𝑉1 +𝑉2 ) = (
𝑇=
𝑇1 𝑇2 (𝑉1 +𝑉2 )
𝑉1 𝑇2 +𝑉2 𝑇1
𝑃𝑉1
𝑅𝑇1
+
𝑃𝑉2
𝑅𝑇2
.
4. Частица массой m = 6,7∙10-27 кг с электрическим зарядом q =
3,2∙10-19 Кл, ускоренная разностью потенциалов U = 10 кВ,
влетает по нормали в «магнитный барьер» протяженностью l =
0,1 м поперек линий магнитной индукции. Величина индукции
однородного магнитного поля в «барьере» B = 30 мТл. Найти
угол, на который отклонится частица от первоначального
направления движения.
Решение: sin 𝜑 =
sin 𝜑 =
𝑙𝑞𝐵
𝑚
𝑚
𝑙
𝑅
,
𝑚𝑣 2
𝑅
= 𝑞𝑣𝐵 , 𝑅 =
√2𝑞𝑈 ≈ 0,147, 𝜑 = 8,4° .
𝑚𝑣
𝑞𝐵
,
𝑚𝑣 2
2
𝑉
𝑉
𝑇1
𝑇2
) 𝑅𝑇 , 𝑉1 +𝑉2 = ( 1 + 2) 𝑇 ,
2𝑞𝑈
= 𝑞𝑈, 𝑣 = √
𝑚
,