Отклонение частиц и световых лучей полем тяготения
реклама

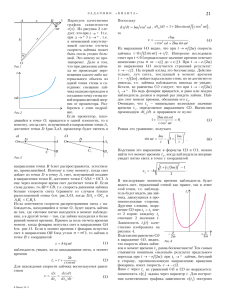
39 ÈÇÈ×ÅÑÊÈÉ ÔÀÊÓËÜÒÀÒÈÂ Ô È Ç ÈÔ × ÅÑÊÈÉ ÔÀÊÓËÜÒÀÒÈ Отклонение частиц и световых лучей полем тяготения îáå ÷àñòè â êâàäðàò è èñïîëüçóÿ òîæäåñòâî 1 cos2 θ ïîëó÷àåì ôîðìóëó (1). Çàïèøåì òåïåðü çàêîíû ñîõðàíåíèÿ ýíåðãèè Å è ìîìåíòà èìïóëüñà L ÷àñòèöû äëÿ ó÷àñòêà À åå òðàåêòîðèè (ñì. ðèñ.1): E A = EB , LA = LB , С.КОЖИНИН èëè 2 Р ÀÑÑÌÎÒÐÈÌ ÍÅÑÊÎËÜÊÎ ÈÍÒÅ- ðåñíûõ çàäà÷ î äâèæåíèè êëàññè÷åñêèõ ÷àñòèö è ôîòîíîâ â ïîëÿõ òÿãîòåíèÿ ïëàíåò è çâåçä. Задача 1. Рассеяние частицы полем Земли Íà êàêîé óãîë θ èçìåíèòñÿ íàïðàâëåíèå ñêîðîñòè ïðîëåòàþùåé ìèìî Çåìëè ìåòåîðíîé ÷àñòèöû ïîä äåéñòâèåì ïîëÿ çåìíîãî òÿãîòåíèÿ (ðèñ.1)? Ñêîðîñòü ÷àñòèöû íà áåñêî- α K mv ∞ r r θ/ O B O 2 2 = O′ 2 b − rm 2brm . (1) Äåéñòâèòåëüíî, ãèïåðáîëà ýòî ãåîìåòðè÷åñêîå ìåñòî òî÷åê, ðàçíîñòü ðàññòîÿíèé äî êîòîðûõ îò äâóõ çàäàííûõ òî÷åê Î è O ′ , íàçûâàåìûõ ôîêóñàìè (ðèñ.2), ïîñòîÿííà: r1 − r2 = const. Îäèí èç ôîêóñîâ ãèïåðáîëû Î ñîâïàäàåò ñ öåíòðîì Çåìëè, âòîðîé ôîêóñ O ′ ëåæèò íà ïðÿìîé, ïðîõîäÿùåé ÷åðåç öåíòð Çåìëè è áëèæàéøóþ ê öåíòðó òî÷êó  òðàåêòîðèè. Íà áåñêî- − 2 GMm rm , (2) bv∞ = rm vm , ãäå vm ñêîðîñòü ÷àñòèöû â òî÷êå Â; ìû ó÷ëè, ÷òî òî÷êà À íàõîäèòñÿ â áåñêîíå÷íîñòè, ïîýòîìó LA = L∞ = = r0 mv∞ sin α 0 = bmv∞ , LB = à o = rm mvm sin 90 = rm mvm . (Îòìåòèì, ÷òî âìåñòî çàêîíà ñîõðàíåíèÿ ìîìåíòà èìïóëüñà ìîæíî èñïîëüçîâàòü âòîðîé çàêîí Êåïëåðà.) Èç ðàâåíñòâ (2) ïîëó÷àåì 2GM 2 v∞ 2 rm − b = 0 . (3) Åñëè ñ÷èòàòü çàäàííûì ðàññòîÿíèå rm , òî äëÿ ïðèöåëüíîãî ðàññòîÿíèÿ b íàõîäèì b = rm 1 + N íå÷íîñòè ðàâíà v∞ . Âëèÿíèå àòìîñôåðû Çåìëè íå ó÷èòûâàòü. Ïðè ðåøåíèè çàäà÷è ó÷òåì (áåç âûâîäà), ÷òî ÷àñòèöà äâèæåòñÿ ïî ãèïåðáîëè÷åñêîé òðàåêòîðèè. Îïèðàÿñü íà ãåîìåòðè÷åñêèå ñâîéñòâà ãèïåðáîëû, ìîæíî äîêàçàòü, ÷òî óãîë ðàññåÿíèÿ θ , ïðèöåëüíîå ðàññòîÿíèå b è ðàññòîÿíèå rm îò öåíòðà ïëàíåòû äî áëèæàéøåé òî÷êè  òðàåêòîðèè ÷àñòèöû ñâÿçàíû ñîîòíîøåíèåì θ 2 θ ϕm M Рис. 1 r mvm = rm + A rm R 2 mv∞ 2 θ B tg b N A b íå÷íî áîëüøèõ ðàññòîÿíèÿõ îò Çåìëè êàê ïðè ïðèáëèæåíèè, òàê è ïðè óäàëåíèè ñêîðîñòü ÷àñòèöû íàïðàâëåíà ïî àñèìïòîòå ãèïåðáîëû, ïîýòîìó çàäà÷à ñîñòîèò â íàõîæäåíèè óãëà θ ìåæäó àñèìïòîòàìè. Òî÷êà ïåðåñå÷åíèÿ àñèìïòîò ëåæèò ïîñåðåäèíå ìåæäó ôîêóñàìè. Ïðèðàâíÿåì ðàçíîñòè ðàññòîÿíèé îò ôîêóñîâ Î è O ′ äî áåñêîíå÷íî óäàëåííîé òî÷êè ýòî îòðåçîê O′ C íà ðèñóí- Ïîëÿðíàÿ îñü K = 1 + tg2 θ , 2GM 2 rm v∞ . Åñëè ñ÷èòàòü çàäàííûì ðàññòîÿíèå b, òî äëÿ rm íàõîäèì rm = Рис. 2 êå 2 è äî áëèæàéøåé ê öåíòðó Çåìëè òî÷êè. Èç òðåóãîëüíèêà OO ′ C íàõîäèì OC = 2b, θ 2b . θ cos 2 Ðàçíîñòü ðàññòîÿíèé îò ôîêóñîâ äî òî÷êè  ñîñòàâëÿåò O ′ C = 2b tg 2 d 2 v∞ F GG GH i ãäå ÂÎ = rm . Òåïåðü óñëîâèå ðàâåíñòâà ðàçíîñòè ðàññòîÿíèé äî âûáðàííûõ òî÷åê ìîæíî çàïèñàòü â âèäå 2b 2b tg = − 2rm . θ 2 cos 2 Ïåðåíîñÿ 2rm â ëåâóþ ÷àñòü, âîçâîäÿ F bv I 1+ G H GM JK 2 ∞ 2 I − 1J . JJ K (4) Äëÿ îïðåäåëåííîñòè áóäåì ñ÷èòàòü èçâåñòíûì ïðèöåëüíûé ïàðàìåòð b. Òîãäà, ñ ó÷åòîì (3), äëÿ óãëà ðàññåÿíèÿ ïîëó÷àåì , OO ′ = BO ′ − BO = OO ′ − BO − BO , θ GM tg θ GM = . 2 bv∞2 (5) Ìåòåîðíàÿ ÷àñòèöà íå çàäåâàåò ïëàíåòó, åñëè rm Ú R (ñì. ðèñ.1). Ïðè rm = = R ðàññòîÿíèå b îêàçûâàåòñÿ ìèíèìàëüíûì è ðàâíûì bmin = R 1 + 2GM 2 Rv∞ = R 1+ Fv I GH v JK 2ê 2 , ∞ ãäå v2 ê = 2GM R âòîðàÿ êîñìè÷åñêàÿ (ïàðàáîëè÷åñêàÿ) ñêîðîñòü. Ïðè çàäàííîì çíà÷åíèè v∞ è ìèíèìàëüíîì ïðèöåëüíîì ðàññòîÿíèè bmin óãîë îòêëîíåíèÿ (èëè óãîë ðàññåÿíèÿ) ìàêñè-