Неопределенный интеграл
реклама

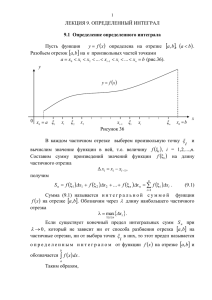
Определенный интеграл 8--1 Основная формула интегрального исчисления 8--2 Методы вычисления определенного интеграла 8-3 Вычисление площадей плоских фигур 8--4 Несобственные интегралы Эпиграф Нет ни одной области математики, … которая когданибудь не окажется применимой к явлениям действительного мира. Н.Лобачевский 2 Основная формула интегрального исчисления Формула ННььююттооннааЛейбница Свойства ооппррееддееллееннннооггоо ииннттееггррааллаа Примеры Формула Ньютона-Лейбница Определенный интеграл на отрезке [a, b] от функции f (x), непрерывной на этом отрезке, есть приращение ее первообразной F(x) на [a, b] : b f ( x)dx F (b) F (a) a Формула Ньютона-Лейбница для вычисления определенного интеграла Обсуждение обозначений Пишут также: b f ( x)dx F ( x) b a F (b) F (a) a Читается «интеграл от a до b эф от икс дэ икс». Числа a и b называются верхним и нижним пределом интегрирования. Функция f(x) называется подынтегральной функцией, - подынтегральным выражением. f(x)dx Различие между интегралами Неопределенный интеграл Определенный интеграл b f ( x)dx f ( x)dx a Функция Число Пример Вычислить определенный 3 интеграл: 2xdx b f ( x)dx F (b) F (a) Подсказка a 1 Решение. 3 2xdx x 2 3 1 32 12 9 1 8 1 Нашли Считаем интеграл первообразную по формуле Н-Л Получили ответ Свойства определенного интеграла Свойство 1. При вычислении можно использовать любую первообразную F(x) + C, в том числе C = 0. b Свойство 2. a f ( x)dx f ( x)dx a b a Свойство 3. f ( x)dx 0 a Нужно уметь проверять свойства непосредственно при помощи формулы НьютонаЛейбница. Свойства определенного интеграла Свойство 4. b c b a a c f ( x)dx f ( x)dx f ( x)dx где c [a, b]. Это означает, что отрезок интегрирования можно разбить на части. Свойство 5. Теорема о среднем (следующий слайд). Нужно уметь проверять свойства непосредственно при помощи формулы НьютонаЛейбница. Свойство 5. Теорема о среднем Теорема. Если функция f (x) непрерывна на отрезке [a, b], то найдется такая точка c [a, b], что: b f ( x)dx f (c)(b a) a Методы интегрирования Применение ффооррммууллыы ННььююттооннаа-Лейбница Замена переменной в ооппррееддееллеенннноомм ииннттееггррааллее Интегрирование «по ччаассттяямм» Замена переменной Замена переменной в определенном интеграле требует и замены пределов интегрирования: (b) b f ( x)dx f ( (t))d (t) a (a ) Условия использования: 1. Функция f (x) непрерывна на отрезке [a, b]. 2. Отрезок [a, b] есть множество значений функции x = имеющей непрерывную производную. (t), Пример Вычислить интеграл: 1 2 3 (1 x ) xdx 0 Решение. t 1 x 2 x 0 1 2 3 1 (1 x ) xdx xdx dt t 1 2 0 2 1 2 2 4 4 t 2 1 15 3 t dt 24 21 8 8 8 1 1 4 Интегрирование по частям b udv (uv) a b a b vdu a Условие использования: Функции u (x) и v (x) имеют непрерывные производные на отрезке [a, b]. Пример Вычислить интеграл: 2 xe dx x 1 Решение. du dx x xe dx e x dx dv v ex 1 u x 2 2 xe x 2 1 e dx 2e e e x 1 2 x 2 1 2e 2 e e 2 e e 2 Вычисление площадей плоских фигур Задача о ппллоощщааддии ккррииввооллииннееййнноойй ттррааппееццииии Составление ииннттееггррааллььнноойй ссууммммыы Классическое определение определенного интеграла Геометрические приложения Задача о площади криволинейной трапеции Область под кривой, ограниченная прямыми x=a и x=b, называется криволинейной трапецией. y y = f (x) y si а b x а xi Площадь si = f (xi) · b x xi Интегральная сумма Пусть функция y = f (x) задана на отрезке [a, b]. Разобьем весь отрезок на n промежутков точками x0, x1, …, xn: a x0 x1 ... xn1 xn b На каждом отрезке разбиения [xi-1, xi] выберем точку сi и положим: xi xi xi 1 Интегральной суммой для функции y = f (x) на отрезке [a, b] n называется: Sn f (ci )xi i 1 Иванов О.В. Кудряшова Л.В. 2005 18 Классическое определение Пусть предел интегральной суммы Sn при стремлении max xi к нулю существует и не зависит от выбора точек x1, x2, … и c1, c2…. Тогда этот предел называется определенным интегралом от функции y = f (x) на отрезке [a, b]: b f ( x)dx a n lim f (c )x max xi 0 i 1 i i Сама функция в этом случае называется интегрируемой (по Риману) на отрезке [a, b]. Пример Найти площадь фигуры, ограниченной линиями y x2 y x yx 2 y x Решение Находим определенный интеграл: 1 S 0 x3\2 x3 1 2 1 | x x dx 3\ 2 3 0 3 Приложения Два примера нахождения площадей Пример Найти площадь, ограниченную линиями y=6–xxy=5 Найти площадь этой фигуры Решение Находим определенный интеграл: 5 5 S 6 x dx x 1 dx 6 x х2 6 dx xdx 5 2 x 1 1 1 5 5 5ln x 15 25 1 30 5ln 5 6 0 12 5ln 5 2 2 |