Площадь криволинейной трапеции

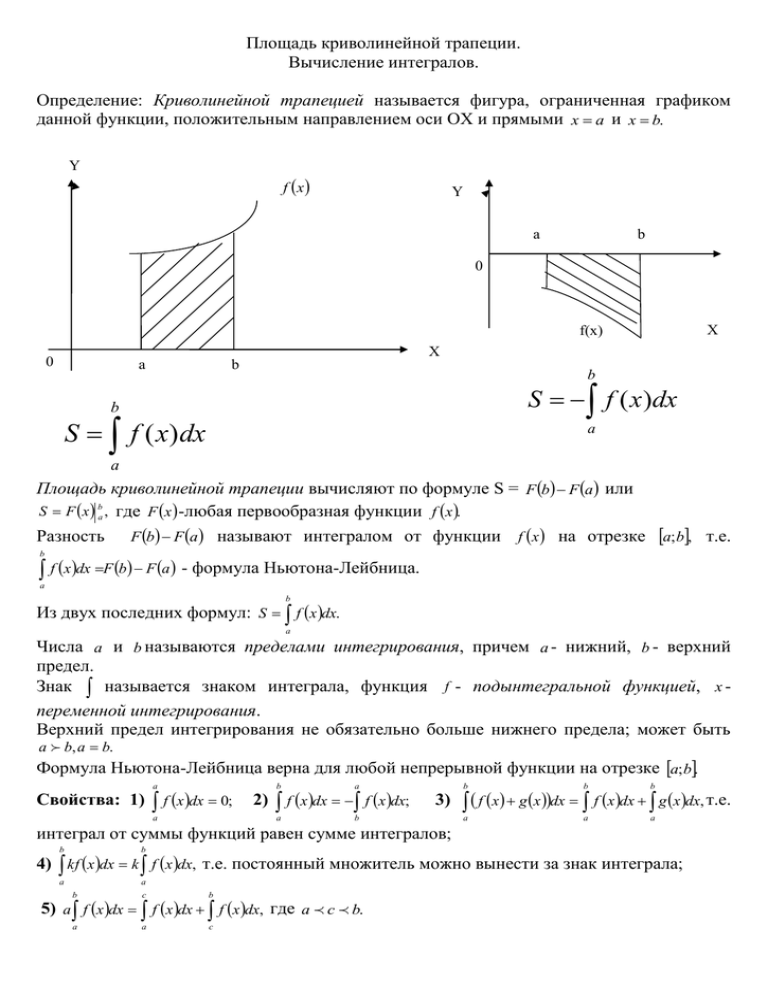
Площадь криволинейной трапеции.
Вычисление интегралов.
Определение: Криволинейной трапецией называется фигура, ограниченная графиком
данной функции, положительным направлением оси ОХ и прямыми x  a и x  b.
Y
f x 
Y
a
b
0
X
f(x)
X
0
a
b
b
S    f ( x)dx
b
S   f ( x)dx
a
a
Площадь криволинейной трапеции вычисляют по формуле S = F b  F a или
S  F x  ba , где F x  -любая первообразная функции f x .
Разность
F b  F a называют интегралом от функции
a;b, т.е.
f x  на отрезке
b
 f xdx F b  F a  - формула Ньютона-Лейбница.
a
b
Из двух последних формул: S   f x dx.
a
Числа a и b называются пределами интегрирования, причем a - нижний, b - верхний
предел.
Знак  называется знаком интеграла, функция f - подынтегральной функцией, x переменной интегрирования.
Верхний предел интегрирования не обязательно больше нижнего предела; может быть
a  b, a  b.
Формула Ньютона-Лейбница верна для любой непрерывной функции на отрезке a;b.
Свойства: 1)
a

f x dx  0;
b
2)

a
a
a
f x dx   f x dx;
3)
b
b
b
b
a
a
a
  f x  g xdx   f xdx   g xdx, т.е.
интеграл от суммы функций равен сумме интегралов;
b
b
4)  kf x dx  k  f x dx, т.е. постоянный множитель можно вынести за знак интеграла;
a
a
b
c
b
a
a
c
5) a  f x dx   f x dx   f x dx, где a  c  b.