О динамике криволинейного движения
реклама

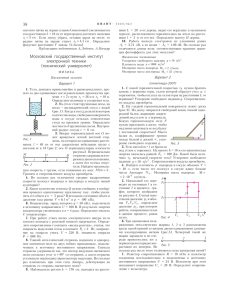
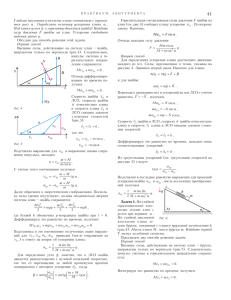
30 Í T ·À 2Á 0 0È 5 /Ò ¹Ó 2 Ð È Å Í Ò À Ï Ð À Ê Ò È ÊÊ ÂÓÀÌ Î äèíàìèêå êðèâîëèíåéíîãî äâèæåíèÿ Â.ÏËÈÑ È Ç ØÊÎËÜÍÎÃÎ ÊÓÐÑÀ ÔÈÇÈÊÈ ÈÇÂÅÑÒÍÎ, ×ÒÎ ÐÀÂ- íîìåðíîå äâèæåíèå ïî îêðóæíîñòè – òàê íàçûâàþò äâèæåíèå ìàòåðèàëüíîé òî÷êè ïî îêðóæíîñòè ñ ïîñòîÿííîé ïî âåëè÷èíå ñêîðîñòüþ – åñòü äâèæåíèå ñ óñêîðåíèåì. Ýòî óñêîðåíèå îáóñëîâëåíî ðàâíîìåðíûì èçìåíåíèåì ñ òå÷åíèåì âðåìåíè íàïðàâëåíèÿ ñêîðîñòè òî÷êè.  ëþáîé ìîìåíò âðåìåíè âåêòîð óñêîðåíèÿ íàïðàâëåí ê öåíòðó îêðóæíîñòè, à åãî âåëè÷èíà ïîñòîÿííà è ðàâíà v2 4π2 = ω2 R = 2 R , an = R T ãäå v – ëèíåéíàÿ ñêîðîñòü òî÷êè, R – ðàäèóñ îêðóæíîñòè, ω – óãëîâàÿ ñêîðîñòü ðàäèóñà-âåêòîðà òî÷êè, Ò – ïåðèîä îáðàùåíèÿ.  ýòîì ñëó÷àå óñêîðåíèå íàçûâàþò öåíòðîñòðåìèòåëüíûì, èëè íîðìàëüíûì, èëè ðàäèàëüíûì. Î÷åâèäíî, ÷òî âîçìîæíî êðèâîëèíåéíîå äâèæåíèå íå òîëüêî ïî îêðóæíîñòè è íå îáÿçàòåëüíî ðàâíîìåðíîå. Ïîãîâîðèì íåìíîãî î êèíåìàòèêå ïðîèçâîëüíîãî êðèâîëèíåéíîãî äâèæåíèÿ. Òåì áîëåå ÷òî â ïðîøëîì ãîäó â ïðîãðàììó âñòóïèòåëüíûõ ýêçàìåíîâ ïî ôèçèêå, íàïðèìåð â ÌÃÓ èì. Ì.Â.Ëîìîíîñîâà, âêëþ÷èëè âîïðîñ îá óñêîðåíèè ìàòåðèàëüíîé òî÷êè ïðè ïðîèçâîëüíîì äâèæåíèè ïî êðèâîëèíåéíîé òðàåêòîðèè. Ðàññìîòðèì ñíà÷àëà íåðàâíîìåðíîå äâèæåíèå ìàòåðèàëüíîé òî÷êè ïî îêðóæíîñòè. Ïðè òàêîì äâèæåíèè èçìåíÿåòñÿ ñî âðåìåíåì íå òîëüêî íàïðàâëåíèå âåêòîðà ñêîðîñòè v , íî è åãî âåëè÷èíà.  ýòîì ñëó÷àå ïðèðà ùåíèå Δv âåêòîðà ñêîðîñòè çà ìàëîå âðåìÿ îò t äî t + Δt óäîáíî ïðåäñòàâèòü â âèäå ñóììû: Δv = Δ v τ + Δ v n (ðèñ.1). Çäåñü Δv τ – êàñàòåëüíàÿ òàíÐèñ. 1 ãåíöèàëüíàÿ ñîñòàâëÿþùàÿ ïðèðàùåíèÿ ñêîðîñòè, ñîíàïðàâëåííàÿ ñ âåêòîðîì ñêîðîñòè è îáóñëîâëåííàÿ ïðèðàùåíèåì âåëè÷èíû âåêòîðà ñêîðîñòè íà Δvτ = Δv cos θ , à Δvn – íîðìàëüíàÿ ñîñòàâëÿþùàÿ, îáóñëîâëåííàÿ (êàê è â ñëó÷àå ðàâíîìåðíîãî äâèæåíèÿ ïî îêðóæíîñòè) âðàùåíèåì âåêòîðà ñêîðîñòè. Òîãäà åñòåñòâåííî è óñêîðåíèå ïðåäñòàâèòü â âèäå ñóììû êàñàòåëüíîé (òàíãåíöèàëüíîé) è íîðìàëüíîé ñîñòàâëÿþùèõ: Δv Δ v τ Δ v n = + = aτ + an . a= Δt Δt Δt Äëÿ ïðîåêöèé âåêòîðà óñêîðåíèÿ íà êàñàòåëüíîå è íîðìàëü- íîå íàïðàâëåíèÿ ñïðàâåäëèâû ñîîòíîøåíèÿ aτ = v2 Δvτ , an = . R Δt Îòìåòèì, ÷òî êàñàòåëüíàÿ ñîñòàâëÿþùàÿ aτ óñêîðåíèÿ õàðàêòåðèçóåò áûñòðîòó èçìåíåíèÿ âåëè÷èíû ñêîðîñòè, à íîðìàëüíàÿ ñîñòàâëÿþùàÿ an õàðàêòåðèçóåò áûñòðîòó èçìåíåíèÿ íàïðàâëåíèÿ ñêîðîñòè. Ïî òåîðåìå Ïèôàãîðà, a = aτ2 + an2 .  ñëó÷àå äâèæåíèÿ ïî ïðîèçâîëüíîé êðèâîëèíåéíîé òðàåêòîðèè âñå óêàçàííûå ñîîòíîøåíèÿ òàêæå ñïðàâåäëèâû, ïðè ýòîì â ôîðìóëå äëÿ íîðìàëüíîãî óñêîðåíèÿ an ïîä âåëè÷èíîé R íàäî ïîíèìàòü ðàäèóñ òàêîé îêðóæíîñòè, ñ ýëåìåíòàðíîé äóæêîé êîòîðîé ñîâïàäàåò ó÷àñòîê êðèâîëèíåéíîé òðàåêòîðèè â ìàëîé îêðåñòíîñòè òîãî ìåñòà, ãäå íàõîäèòñÿ äâèæóùàÿñÿ ìàòåðèàëüíàÿ òî÷êà. Âåëè÷èíó R íàçûâàþò ðàäèóñîì êðèâèçíû òðàåêòîðèè â äàííîé òî÷êå. Òåïåðü ðàññìîòðèì íåñêîëüêî êîíêðåòíûõ çàäà÷ íà êðèâîëèíåéíîå äâèæåíèå, ïðåäëàãàâøèõñÿ â ïîñëåäíèå ãîäû íà âñòóïèòåëüíûõ ýêçàìåíàõ è îëèìïèàäàõ ïî ôèçèêå â âåäóùèõ âóçàõ ñòðàíû. Çàäà÷à 1. Êàìåíü áðîøåí ñî ñêîðîñòüþ v0 ïîä óãëîì α ê ãîðèçîíòó. Íàéäèòå ðàäèóñ R êðèâèçíû òðàåêòîðèè â îêðåñòíîñòè òî÷êè ñòàðòà. Óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ g èçâåñòíî. Äëÿ îòâåòà íà âîïðîñ çàäà÷è âîñïîëüçóåìñÿ ñîîòíîøåíèåì äëÿ íîðìàëüíîãî óñêîðåíèÿ: an = v2 . R  ìàëîé îêðåñòíîñòè òî÷êè ñòàðòà v = v0 (ðèñ.2). Íîðìàëüíîå óñêîðåíèå an åñòü ïðîåêöèÿ óñ êîðåíèÿ ñâîáîäíîãî ïàäåíèÿ g íà íîðìàëü ê òðàåêòîðèè: an = g cos α . Ýòî äàåò R= v02 . g cos α Çàäà÷à 2. Îïðåäåëèòå âåñ Ð òåëà ìàññîé m íà ãåîãðàôè÷åñêîé øèðîòå ϕ . Óñêîðåíèå, ñîîáùàåìîå ñèëîé òÿæåñòè, ðàâ- Ðèñ. 2 íî g. Çåìëþ ñ÷èòàéòå îäíîðîäíûì øàðîì ðàäèóñîì R. Íàïîìíèì, ÷òî âåñ òåëà P – ýòî ñèëà, îáóñëîâëåííàÿ òÿãîòåíèåì, ñ êîòîðîé òåëî äåéñòâóåò íà îïîðó èëè ïîäâåñ. Äîïóñòèì, ÷òî òåëî ëåæèò íà ïîâåðõíîñòè âðàùàþùåéñÿ Çåìëè. Íà íåãî äåéñòâóþò ñèëà òÿæåñòè mg, íàïðàâëåííàÿ ê öåíòðó Çåìëè, è ñèëà ðåàêöèè îïîðû N (ðèñ.3). Ïî òðåòüåìó Íüþ çàêîíó òîíà, P = - N . Ïîýòîìó äëÿ îïðåäåëåíèÿ âåñà òåëà íàéäåì ñèëó ðåàêöèè N .  èíåðöèàëüíîé ñèñòåìå îòñ÷åòà, öåíòð êîòîðîé íàõîäèòñÿ â öåíòðå Çåìëè, òåëî ðàâíîìåðíî äâèæåòñÿ ïî îêðóæíîñòè ðàäèóñîì r = R cos ϕ ñ ïåðèîäîì îäíè ñóòêè, ò.å. Ò = Ðèñ. 3 ÏÐÀÊÒÈÊÓÌ = 86400 ñ, è öèêëè÷åñêîé ÷àñòîòîé 2π ω= = 7, 3 ◊ 10 -5 c -1 . T Óñêîðåíèå òåëà ïî âåëè÷èíå ðàâíî an = ω2r = ω2 R cos ϕ è íàïðàâëåíî ê îñè âðàùåíèÿ Çåìëè. Èç ýòîãî ñëåäóåò, ÷òî ðàâíîäåéñòâóþùàÿ ñèë òÿæåñòè è ðåàêöèè îïîðû òîæå äîëæíà áûòü íàïðàâëåíà ê îñè âðàùåíèÿ Çåìëè. Òîãäà ïðè 0 < ϕ < π 2 ñèëà ðåàêöèè îáðàçóåò ñ ïåðïåíäèêóëÿðîì ê îñè âðàùåíèÿ íåêîòîðûé óãîë α π ϕ . Ïî âòîðîìó çàêîíó Íüþòîíà, ma = mg + N . Ïåðåéäåì ê ïðîåêöèÿì ñèë è óñêîðåíèÿ íà ðàäèàëüíîå íàïðàâëåíèå: mω2 R cos ϕ = mg cos ϕ - N cos α è íà íàïðàâëåíèå, ïåðïåíäèêóëÿðíîå ïëîñêîñòè, â êîòîðîé ïðîèñõîäèò äâèæåíèå: 0 = -mg sin ϕ + N sin α . Èñêëþ÷àÿ α èç äâóõ ïîñëåäíèõ ñîîòíîøåíèé, íàõîäèì âåñ òåëà, ïîêîÿùåãîñÿ íà âðàùàþùåéñÿ Çåìëå: P=N= (mg)2 - m2ω2R (2g - ω2 R) cos2 ϕ . Çàäà÷à 3. Ðàññòîÿíèå îò Çåìëè äî äâîéíîé çâåçäû â ñîçâåçäèè Öåíòàâðà ðàâíî L = 2,62 ◊ 10 5 à.å. Íàáëþäàåìîå óãëîâîå ðàññòîÿíèå ìåæäó çâåçäàìè ïåðèîäè÷åñêè èçìåíÿåòñÿ ñ ïåðèîäîì Ò = 80 ëåò è äîñòèãàåò íàèáîëüøåãî çíà÷åíèÿ ϕ = 0,85 ◊ 10 -5 ðàä. Îïðåäåëèòå ñóììàðíóþ ìàññó Ì çâåçä. Ïîñòîÿííàÿ âñåìèðíîãî òÿãîòåíèÿ G = 6,67 ◊ 10 -11 (m ◊ ì 2 *ã2 ) , 1 =. = 1,5 ◊ 1011 ì . Îðáèòû çâåçä ñ÷èòàéòå êðóãîâûìè. Ïîä äåéñòâèåì ãðàâèòàöèîííûõ ñèë m1m2 F1 = F2 = G (r1 + r2 )2 çâåçäû äâèæóòñÿ ðàâíîìåðíî ñ ïåðèîäîì Ò ïî îêðóæíîñòÿì ðàäèóñîâ r1 è r2 âîêðóã öåíòðà ìàññ ñèñòåìû ñî ñêîðîñòÿìè v1 è v2 ñîîòâåòñòâåííî (ðèñ.4). Ïî âòîðîìó çàêîíó Íüþòîíà, m1v12 m1m2 =G , r1 (r1 + r2 )2 m2v22 m1m2 =G . r2 (r1 + r2 )2 Ñëîæèâ ýòè ðàâåíñòâà (ïîñëå ñîêðàùåíèÿ íà m1 è m2 ñîîòâåòñòâåííî), ïîëó÷èì G Ðèñ. 4 m1 + m2 (r1 + r2 ) 2 = v12 r1 + v22 r2 . Îòñþäà ñ ó÷åòîì ñîîòíîøåíèé r1 + r2 = Lϕ , v1 = 2πr1 2πr2 , v2 = T T ïðèõîäèì ê îòâåòó 2 3 3 Ê 2π ˆ L ϕ M = m1 + m2 = Á ˜ ª 3,5 ◊ 1027 *ã . ËT¯ G Çàäà÷à 4. Íà ãîðèçîíòàëüíîé ïëàòôîðìå ñòîèò ñîñóä ñ âîäîé (ðèñ.5).  ñîñóäå çàêðåïëåí òîíêèé ñòåðæåíü ÀÂ, 31 ÀÁÈÒÓÐÈÅÍÒÀ íàêëîíåííûé ê ãîðèçîíòó ïîä óãëîì α . Îäíîðîäíûé øàðèê ðàäèóñîì R ìîæåò ñêîëüçèòü áåç òðåíèÿ âäîëü ñòåðæíÿ, ïðîõîäÿùåãî ÷åðåç åãî öåíòð. Ïëîòíîñòü ìàòåðèàëà øàðèêà ρ0 , ïëîòíîñòü âîäû ρ , ρ0 < ρ . Ïðè âðàùåíèè ñèñòåìû ñ ïîñòîÿííîé óãëîâîé ñêîðîñòüþ âîêðóã âåðòèêàëüíîé îñè, ïðîõîäÿùåé ÷åðåç íèæíèé êîíåö À ñòåðæíÿ, öåíòð øàðèêà óñòàíàâëèâàåòñÿ íà ðàññòîÿíèè L îò ýòîãî êîíöà. Ñ êàêîé ïî âåëè÷èíå ñèëîé F øàðèê äåéñòâóåò íà ñòåðæåíü? Êàêîâà óãëîâàÿ ñêîðîñòü ω âðàùåíèÿ ïëàòôîðìû? Ïðè êàêîé ìèíèìàëüíîé óãëîâîé ñêîðîñòè ωmin øàðèê «óòîíåò», ò.å. îêàæåòñÿ ó äíà ñîñóäà? Îáîçíà÷èì îáúåì øàðè4 êà V ( V = πR3 ). Íà øà3 ðèê áóäóò äåéñòâîâàòü òðè ñèëû: ñèëà òÿæåñòè ρ0Vg , ñèëà íîðìàëüíîé ðåàêöèè N ñî ñòîðîíû ñòåðæíÿ Ðèñ. 5 (øàðèê äåéñòâóåò íà ñòåðæåíü ñ òàêîé æå ïî âåëè÷èíå è ïðîòèâîïîëîæíîé ïî íàïðàâëåíèþ ñèëîé) è ñèëà Àðõèìåäà FA . Íàéäåì àðõèìåäîâó ñèëó. Ðàññìîòðèì äâèæåíèå æèäêîñòè â îòñóòñòâèå øàðèêà. Ëþáîé ýëåìåíòàðíûé îáúåì âîäû ðàâíîìåðíî äâèæåòñÿ ïî îêðóæíîñòè ðàäèóñîì r â ãîðèçîíòàëüíîé ïëîñêîñòè. Ñëåäîâàòåëüíî, âåðòèêàëüíàÿ ñîñòàâëÿþùàÿ ñóììû ñèë äàâëåíèÿ (ñèëû Àðõèìåäà) óðàâíîâåøèâàåò ñèëó òÿæåñòè, äåéñòâóþùóþ íà æèäêîñòü â ðàññìàòðèâàåìîì îáúåìå, à ãîðèçîíòàëüíàÿ ñîñòàâëÿþùàÿ ñîîáùàåò ýòîé æèäêîñòè öåíòðîñòðåìèòåëüíîå óñêîðåíèå an = ω2r . Ïðè çàìåùåíèè æèäêîñòè øàðèêîì ýòè ñîñòàâëÿþùèå íå èçìåíÿþòñÿ, à ñèëà, äåéñòâóþùàÿ íà âîäÿíîé øàðèê ñî ñòîðîíû òîíêîãî ñòåðæíÿ, ðàâíà íóëþ. Òîãäà âåðòèêàëüíàÿ ñîñòàâëÿþùàÿ ñèëû Àðõèìåäà ïî âåëè÷èíå ðàâíà ñèëå òÿæåñòè âîäÿíîãî øàðà: FA z = ρVg , à íàïðàâëåííàÿ ê îñè âðàùåíèÿ ñîñòàâëÿþùàÿ ñèëû Àðõèìåäà ñîîáùàåò âîäÿíîìó øàðó öåíòðîñòðåìèòåëüíîå óñêîðåíèå an = ω2L cos α è ïî âåëè÷èíå ðàâíà FA n = ρVω2 L cos α . Ïîä äåéñòâèåì ïðèëîæåííûõ ñèë øàðèê äâèæåòñÿ ðàâíîìåðíî ïî îêðóæíîñòè ðàäèóñîì L cos α â ãîðèçîíòàëüíîé ïëîñêîñòè (ðèñ.6). Ïî âòîðîìó çàêîíó Íüþòîíà, ma = mg + N + FA . Ðèñ. 6 Ïåðåõîäÿ ê ïðîåêöèÿì ñèë è óñêîðåíèé íà âåðòèêàëüíóþ îñü, íàõîäèì ρVg - ρ0Vg - N cos α = 0 . Ïðîåêòèðóÿ ñèëû è óñêîðåíèÿ â ãîðèçîíòàëüíîé ïëîñêîñòè íà ðàäèàëüíîå íàïðàâëåíèå, ïîëó÷àåì ρ0VLω2 cos α = ρVLω2 cos α - N sin α . Èç äâóõ ïîñëåäíèõ ñîîòíîøåíèé îïðåäåëÿåì âåëè÷èíó ñèëû íîðìàëüíîé ðåàêöèè ñòåðæíÿ, à çíà÷èò, è ñèëó äàâëåíèÿ (Ïðîäîëæåíèå ñì. íà ñ. 34) ÊÂÀÍT· 2005/¹2 34 (Íà÷àëî ñì. íà ñ. 30) øàðèêà íà ñòåðæåíü: F= N= (ρ - ρ0 ) Vg cos α è óãëîâóþ ñêîðîñòü: g tg α . L cos α Êàê âèäèì, ñ ðîñòîì óãëîâîé ñêîðîñòè ω ðàññòîÿíèå L óìåíüøàåòñÿ.  ìîìåíò, êîãäà øàð ïðèáëèçèòñÿ êî äíó, R , ïðè ýòîì L= sin α g tg α . ωmin = R Çàäà÷à 5. Îäíîðîäíóþ öåïî÷êó äëèíîé L ïîìåñòèëè íà ãëàäêóþ ñôåðè÷åñêóþ ïîâåðõíîñòü ðàäèóñîì R òàê, ÷òî îäèí åå êîíåö çàêðåïëåí íà âåðøèíå ñôåðû. Âåðõíèé êîíåö öåïî÷êè îñâîáîæäàþò. Ñ êàêèì ïî âåëè÷èíå óñêîðåíèåì aτ áóäåò äâèãàòüñÿ ñðàçó ïîñëå îñâîáîæäåíèÿ êàæäûé ýëåìåíò öåïî÷êè? Ìàññà åäèíèöû äëèíû öåïî÷êè ρ . Óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ g. Ðàññìîòðèì ýëåìåíòàðíûé ó÷àñòîê öåïî÷êè äëèíîé ΔL = RΔϕ (ðèñ.7). Åãî ìàññà ðàâíà Δm = ρΔL . Ñèëû, äåéñòâóþùèå íà âûäåÐèñ. 7 ëåííûé ó÷àñòîê, ïîêàçàíû íà ðèñóíêå. Ïî âòîðîìó çàêîíó Íüþòîíà, Δma = T (ϕ + Δϕ) + T (ϕ) + Δmg + Δ N . ω= Ïåðåõîäÿ ê ïðîåêöèÿì ñèë è óñêîðåíèé íà êàñàòåëüíîå íàïðàâëåíèå, ïîëó÷àåì Δmaτ = T (ϕ + Δϕ) - T (ϕ) + Δmg sin ϕ . Ïåðåïèøåì ïîëó÷åííîå ñîîòíîøåíèå â âèäå ΔT = ρR (aτ - g sin ϕ) Δϕ . Ïðîñóììèðóåì ïðèðàùåíèÿ ñèëû íàòÿæåíèÿ ïî âñåé äëèíå öåïî÷êè:  ΔT = ρR (aτ - g sin ϕ) Δϕ . Òåïåðü ó÷òåì, ÷òî íà ñâîáîäíûõ êîíöàõ öåïî÷êè ñèëû  ΔT = 0 , ÷òî óñêîðåíèå L îäèíàêîâî ó âñåõ ýëåìåíòàðíûõ ôðàãìåíòîâ,  Δϕ = , R íàòÿæåíèÿ îáðàùàþòñÿ â íîëü, ò.å. aτ Δ (cos ϕ) = - sin ϕ Δϕ , è ïîëó÷èì RÊ Lˆ Á1 - cos ˜¯ . LË R Çàäà÷à 6. Âåäóùèå êîëåñà ïàðîâîçà ñîåäèíåíû ðåå÷íîé ïåðåäà÷åé, îäíî çâåíî êîòîðîé ïðåäñòàâëÿåò ñîáîé ïëîñêóþ ãîðèçîíòàëüíóþ øòàíãó, øàðíèðíî ïðèêðåïëåííóþ ê ñïèöàì ñîñåäíèõ êîëåñ íà ðàññòîÿíèè R/2 îò îñè, ãäå R – ðàäèóñ êîëåñà. Ïðè îñìîòðå ïàðîâîçà ìåõàíèê ïîñòàâèë íà ýòó øòàíãó ÿùèê è ïî ðàññåÿííîñòè çàáûë åãî òàì. Ïàðîâîç òðîãàåòñÿ ñ ìåñòà è î÷åíü ìåäëåííî íàáèðàåò ñêîðîñòü. Îöåíèòå ñêîðîñòü v1 ïàðîâîçà, ïðè êîòîðîé ÿùèê íà÷íåò ïðîñêàëüçûâàòü îòíîñèòåëüíî øòàíãè. Êîýôôèöèåíò òðåíèÿ ñêîëüæåíèÿ ÿùèêà ïî øòàíãå μ = 0,4 , ðàäèóñ êîëåñà R = 0,8 ì, óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ g = 10 ì “2 . aτ = g Ïåðåéäåì â ñèñòåìó îòñ÷åòà, ñâÿçàííóþ ñ ïàðîâîçîì (ðèñ.8). Ïîñêîëüêó ðàçãîí ïðîèñõîäèò î÷åíü ìåäëåííî, ýòó ñèñòåìó ìîæíî ñ÷èòàòü èíåðöèàëüíîé. Äî íà÷àëà ïðîñêàëüçûâàíèÿ ÿùèê äâèæåòñÿ Ðèñ. 8 ïî îêðóæíîñòè ðàäèóñîì r = R/2. Ïî âòîðîìó çàêîíó Íüþòîíà, ma = mg + N + F2! . Âåêòîð óñêîðåíèÿ ÿùèêà íàïðàâëåí ê öåíòðó îêðóæíîñòè è ïî âåëè÷èíå ðàâåí a = ω2r , ãäå ω – óãëîâàÿ ñêîðîñòü âðàùåíèÿ êîëåñ ïàðîâîçà. Îáîçíà÷èì óãîë, êîòîðûé âåêòîð óñêîðåíèÿ îáðàçóåò â äàííûé ìîìåíò âðåìåíè ñ ãîðèçîíòîì, áóêâîé β . Ïåðåõîäÿ ê ïðîåêöèÿì ñèë è óñêîðåíèÿ íà ãîðèçîíòàëüíóþ è âåðòèêàëüíóþ îñè, ñ ó÷åòîì òîãî, ÷òî F2! £ μN , ïîëó÷àåì mω2r cos β £ μN , mω2r sin β = mg - N . Èñêëþ÷èâ îòñþäà ñèëó ðåàêöèè îïîðû, ïðèõîäèì ê íåðàâåíñòâó ω2r (cos β + μ sin β) £ μg . Íàèáîëüøåå çíà÷åíèå âûðàæåíèÿ cos β + μ sin β = 1 + μ2 cos (β - α ) , ãäå óãîë α òàêîâ, ÷òî cos α = 1 è sin α = μ , 1 + μ2 1+ μ äîñòèãàåòñÿ ïðè β = α è ðàâíî 1 + μ2 . Äâèæåíèå ãðóçà áóäåò ïðîèñõîäèòü áåç ïðîñêàëüçûâàíèÿ äî òåõ ïîð, ïîêà óãëîâàÿ ñêîðîñòü âðàùåíèÿ êîëåñ ïàðîâîçà áóäåò óäîâëåòâîðÿòü íåðàâåíñòâó μg ω£ . r 1 + μ2 2 Îòñþäà äëÿ èñêîìîé ñêîðîñòè ïàðîâîçà v1 ïîëó÷àåì v1 = ωR = 2μgR 1 + μ2 ª 2, 4 ì “ . Çàäà÷à 7. Ãëàäêèé æåëîá ñîñòîèò èç ãîðèçîíòàëüíîé ÷àñòè À è äóãè îêðóæíîñòè BD ðàäèóñîì R = 5 ì (ðèñ.9). Øàéáà ñêîëüçèò ïî ãîðèçîíòàëüíîé ÷àñòè ñî ñêîðîñòüþ v0 = 10 ì “ . Îïðåäåëèòå âåëè÷èíó óñêîðåíèÿ øàéáû â òî÷êå Ñ è óãîë β , êîòîðûé âåêòîð a óñêîðåíèÿ øàéáû â ýòîò ìîìåíò ñîñòàâëÿåò ñ íèòüþ. Ðàäèóñ ÎÑ îáðàçóåò ñ âåðòèêàëüþ óãîë α = 60∞ . Óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ g = = 10 ì “2 . Äëÿ íàõîæäåíèÿ óñêî- Ðèñ. 9 ðåíèÿ øàéáû â òî÷êå Ñ íàéäåì òàíãåíöèàëüíóþ aτ è íîðìàëüíóþ an âåëè÷èíû ñîñòàâëÿþùèõ óñêîðåíèÿ â ýòîé òî÷êå. Íà òåëî, äâèæóùååñÿ â âåðòèêàëüíîé ïëîñêîñòè ïî äóãå BD, â ëþáîé òî÷êå äåéñòâóþò ñèëû òÿæåñòè mg è ðåàêöèè ÏÐÀÊÒÈÊÓÌ îïîðû N . Ïî âòîðîìó çàêîíó Íüþòîíà, ma = mg + N . èñêîìîãî âðåìåíè ïîëó÷àåì T= Ïåðåéäåì ê ïðîåêöèÿì ñèë è óñêîðåíèÿ íà òàíãåíöèàëüíîå íàïðàâëåíèå: 2 maτ = -mg sin α , îòêóäà aτ = - g sin α ª -8,7 ì “ . Äëÿ îïðåäåëåíèÿ íîðìàëüíîé ñîñòàâëÿþùåé óñêîðåíèÿ íàéäåì âåëè÷èíó v ñêîðîñòè øàéáû â òî÷êå Ñ (ïîñêîëüêó an = v2 R ). Îáðàòèìñÿ ê ýíåðãåòè÷åñêèì ñîîáðàæåíèÿì. Ïîòåíöèàëüíóþ ýíåðãèþ øàéáû íà ãîðèçîíòàëüíîé ÷àñòè æåëîáà áóäåì ñ÷èòàòü ðàâíîé íóëþ. Òîãäà, ïî çàêîíó ñîõðàíåíèÿ ïîëíîé ìåõàíè÷åñêîé ýíåðãèè, v2 v2 m 0 =m + mgR (1 - cos α ) , 2 2 îòêóäà v2 v02 an = = - 2g (1 - cos α ) = 10 ì “2 . R R Âåëè÷èíó óñêîðåíèÿ øàéáû â òî÷êå Ñ íàéäåì ïî òåîðåìå Ïèôàãîðà: a = aτ2 + an2 ª 13,2 ì “2 .  òî÷êå Ñ âåêòîð óñêîðåíèÿ a îáðàçóåò ñ íèòüþ óãîë β òàêîé, ÷òî aτ ª 0,87 , îòêóäà β ª 41∞ . an Çàäà÷à 8. Ïî ãëàäêîé ïðîâîëî÷íîé âèíòîâîé ëèíèè ðàäèóñîì R ñ øàãîì h, îñü êîòîðîé âåðòèêàëüíà, ñêîëüçèò ñ íóëåâîé íà÷àëüíîé ñêîðîñòüþ áóñèíêà ìàññîé m. Çà êàêîå âðåìÿ Ò áóñèíêà îïóñòèòñÿ ïî âåðòèêàëè íà Í? Ñ êàêîé ïî âåëè÷èíå F ñèëîé áóñèíêà äåéñòâóåò íà ïðîâîëîêó â ýòîò ìîìåíò? Óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ g. Íà áóñèíêó äåéñòâóþò ñèëû òÿæåñòè mg è íîðìàëüíîé ðåàêöèè N = N1 + N2 , ãäå N1 íàïðàâëåíà ãîðèçîíòàëüíî (ïåðïåíäèêóëÿðíî ïëîñêîñòè ðèñóíêà 10), à N2 ëåæèò â îäíîé Ðèñ. 10 ïëîñêîñòè ñ âåêòîðàìè mg è v . Äëÿ îòâåòà íà âîïðîñû çàäà÷è íàéäåì êàñàòåëüíóþ è íîðìàëüíóþ ñîñòàâëÿþùèå óñêîðåíèÿ. Ïî âòîðîìó çàêîíó Íüþòîíà, ma = mg + N1 + N2 . tg β = Ïåðåõîäÿ ê ïðîåêöèÿì ñèë è óñêîðåíèÿ íà êàñàòåëüíîå íàïðàâëåíèå, íàõîäèì aτ = g sin α . Çäåñü α – óãîë íàêëîíà âåêòîðà ñêîðîñòè ê ãîðèçîíòó òàêîé, ÷òî h sin α = . 2 2 4π R + h2 Ïî çàêîíó ñîõðàíåíèÿ ýíåðãèè, v2 = mgH , è v = 2gH . 2 Êàñàòåëüíàÿ ñîñòàâëÿþùàÿ óñêîðåíèÿ ïîñòîÿííà, íà÷àëüíàÿ ñêîðîñòü ðàâíà íóëþ, ñëåäîâàòåëüíî, ìîäóëü âåêòîðà ñêîðîñòè ðàñòåò ñî âðåìåíåì ïî ëèíåéíîìó çàêîíó. Îòñþäà äëÿ m 35 ÀÁÈÒÓÐÈÅÍÒÀ 2gH v = = aτ g sin α ( 2H 4π2 R2 + h2 gh2 ). Äëÿ îïðåäåëåíèÿ íîðìàëüíîé ñîñòàâëÿþùåé óñêîðåíèÿ ïåðåéäåì â ïîäâèæíóþ ñèñòåìó îòñ÷åòà, ïîñòóïàòåëüíî äâèæóùóþñÿ îòíîñèòåëüíî ëàáîðàòîðèè ïî âåðòèêàëè âíèç ñî ñêîðîñòüþ v sin α .  ýòîé ñèñòåìå áóñèíêà óñêîðåííî äâèæåòñÿ ïî îêðóæíîñòè ðàäèóñîì R ñî ñêîðîñòüþ v cos α , ïðè ýòîì íîðìàëüíàÿ ñîñòàâëÿþùàÿ óñêîðåíèÿ áóñèíêè ïî âåëè2 ÷èíå ðàâíà an = (v cos α ) R . Òàê êàê óñêîðåíèå ïîäâèæíîé ñèñòåìû ñîíàïðàâëåíî ñ g , íîðìàëüíàÿ ñîñòàâëÿþùàÿ óñêîðåíèÿ áóñèíêè ïðè ïåðåõîäå â ëàáîðàòîðíóþ ñèñòåìó îòñ÷åòà íå èçìåíèòñÿ (ýòî ñëåäóåò èç ïðàâèëà ñëîæåíèÿ óñêîðåíèé). Èç âòîðîãî çàêîíà Íüþòîíà íàõîäèì ñîñòàâëÿþùèå ñèëû, ñ êîòîðîé ïðîâîëîêà äåéñòâóåò íà áóñèíêó: (v cos α)2 = mg 2H cos2 α N1 = m , N2 = mg cos α , R R 2πR ãäå cos α = . 2 2 4 π R + h2 Ïî òðåòüåìó çàêîíó Íüþòîíà áóñèíêà äåéñòâóåò íà ïðîâîëî êó ñèëîé F = - N1 + N2 , âåëè÷èíà (ìîäóëü) êîòîðîé ðàâíà ( F= N12 + N22 = mg ) 2πR 4π2 R2 + h2 4π2 R2 + h2 + 16π2 H 2 . Óïðàæíåíèÿ 1. Ñôåðè÷åñêèé âîçäóøíûé øàð ðàäèóñîì R = 5 ì óäåðæèâàåòñÿ âåðòèêàëüíîé âåðåâêîé, åãî öåíòð íàõîäèòñÿ íà âûñîòå Í = = 6 ì íàä ãîðèçîíòàëüíîé ïîâåðõíîñòüþ. Ñ ýòîé ïîâåðõíîñòè áðîñàþò êàìåíü òàê, ÷òî îí ïåðåëåòàåò øàð, ïî÷òè êàñàÿñü åãî â âåðõíåé òî÷êå. Ñ êàêîé ìèíèìàëüíîé ñêîðîñòüþ v0 ñëåäóåò áðîñàòü êàìåíü è íà êàêîì ðàññòîÿíèè s îò öåíòðà øàðà áóäåò íàõîäèòüñÿ â ýòîì ñëó÷àå òî÷êà áðîñàíèÿ? Óêàçàíèå: óñêîðåíèå ñâîáîäíîãî ïàäåíèÿ ó ïîâåðõíîñòè Çåìëè â ýòîé è ïîñëåäóþùèõ çàäà÷àõ ðàâíî g = 10 ì “2 . 2. Èçâåñòíî, ÷òî ñïóòíèê, íàõîäÿùèéñÿ íà îðáèòå, âûñîòà êîòîðîé h = 3,6 ◊ 104 *ì , îáðàùàåòñÿ âîêðóã Çåìëè çà îäíè ñóòêè è ìîæåò «âèñåòü» íàä îäíîé è òîé æå òî÷êîé ýêâàòîðà. Äîïóñòèì, ÷òî îáñóæäàåòñÿ âîïðîñ î çàïóñêå íà òàêóþ æå âûñîòó ñïóòíèêà, êîòîðûé áóäåò «âèñåòü» íàä Ñàíêò-Ïåòåðáóðãîì. Êàêóþ ïî âåëè÷èíå è íàïðàâëåíèþ ñèëó òÿãè F äîëæåí ðàçâèâàòü äâèãàòåëü ñïóòíèêà, ÷òîáû óäåðæèâàòü åãî íà çàäàííîé îðáèòå? Ìàññà ñïóòíèêà m = 103 *ã , Ñàíêò-Ïåòåðáóðã íàõîäèòñÿ íà øèðîòå ϕ = 60∞ , ðàäèóñ Çåìëè R = 6,4 ◊ 10 3 *ì . 3. Ïî ãëàäêîìó ñòîëó äâèæóòñÿ äâà òåëà c ìàññàìè m1 è m2 , ñîåäèíåííûå ëåãêîé íåðàñòÿæèìîé íèòüþ äëèíîé L.  íåêîòîðûé ìîìåíò ïåðâîå òåëî îñòàíàâëèâàåòñÿ, à ñêîðîñòü âòîðîãî ðàâíà v è ïåðïåíäèêóëÿðíà íèòè. Íàéäèòå ñèëó Ò íàòÿæåíèÿ íèòè. 4. Îäíîðîäíóþ öåïî÷êó ìàññîé m è äëèíîé L ïîìåñòèëè íà ãëàäêóþ ñôåðè÷åñêóþ ïîâåðõíîñòü ðàäèóñîì R = 4L òàê, ÷òî îäèí åå êîíåö çàêðåïëåí íà âåðøèíå ñôåðû. Âåðõíèé êîíåö öåïî÷êè îñâîáîæäàþò. Íàéäèòå íàèáîëüøóþ âåëè÷èíó Tmax ñèëû íàòÿæåíèÿ öåïî÷êè ñðàçó ïîñëå åå îñâîáîæäåíèÿ. Óêàçàíèå: äëÿ ðàññìàòðèâàåìûõ â çàäà÷å óãëîâ ñ÷èòàéòå sin α ª α , cos α ª 1 - α2 2 . 5.  çàäà÷å 6 èç òåêñòà ñòàòüè íàéäèòå ñêîðîñòü v2 , ïðè êîòîðîé ÿùèê íà÷íåò ïîäïðûãèâàòü. 6. Äëÿ ýêîíîìèè ìåñòà âúåçä íà îäèí èç âûñî÷àéøèõ â ßïîíèè ìîñòîâ óñòðîåí â âèäå âèíòîâîé ëèíèè, îáâèâàþùåé öèëèíäð ðàäèóñîì R. Ïðè äâèæåíèè ïî òàêîé äîðîãå âåêòîð ñêîðîñòè àâòîìîáèëÿ ñîñòàâëÿåò óãîë α ñ ãîðèçîíòàëüíîé ïëîñêîñòüþ. Íàéäèòå íàïðàâëåíèå è âåëè÷èíó ñóììû ñèë, äåéñòâóþùèõ íà àâòîìîáèëü ìàññîé m, äâèæóùèéñÿ ïî òàêîé äîðîãå ñ ïîñòîÿííîé ïî âåëè÷èíå ñêîðîñòüþ v. Îñü âèíòîâîé ëèíèè âåðòèêàëüíà.