Переходные процессы
реклама

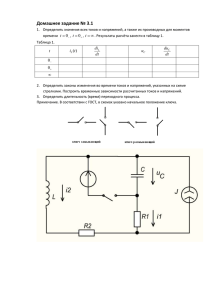
Переходные процессы - классический подход Ранее : рассмотрение цепей с постоянными элементами и с источниками постоянной или строго периодической ЭДС - расчет т.н. стационарных процессов. Но часто - нестационарные процессы, вызванные изменением параметров цепи (конфигурации, величин ЭДС, т.д.) - т.н. переходные процессы. Такое изменение параметров цепи (переход от одного режима работы к другому) называется коммутацией и вызывает переходной процесс - переход токов и напряжений от исходных значений (возникших в момент коммутации) к установившимся. Процесс коммутации часто считается мгновенным. Переходной процесс в общем случае неограниченно долог - но обычно считают завершенным при уменьшении отличия от нового стационарного процесса до заданной величины (например, до 1%). Переходной процесс всегда мгновенный только для цепей без реактивностей (нет "памяти"). Li 2 Cu 2 При наличии L , C энергии WL = и WC = не могут меняться мгновенно 2 2 - т.к. мощности в цепи не могут быть бесконечно велики - и переходного процесса нет, только если энергии (точнее - токи в индуктивностях и напряжения на емкостях), запасенные на момент коммутации уже соответствуют установившемуся режиму. Практически - переходные процессы как вредны (искрение в розетках и выключателях, экстратоки, т.д.), так и полезны (в импульсном формирователе основной режим работы). Для переходных процессов в линейных цепях - линейные дифференциальные уравнения; порядок уравнения = числу независимых "запасателей энергии" в цепи (т.е. таких, которые нельзя заменить одним реактивным элементом): Для решения необходимы так же начальные условия - и для порядка выше первого знание и токов, и напряжений в начальный момент времени (или токов и их производных по времени, или напряжений и их производных). ⇒ первый этап - определение начальных условий применением законов коммутации : Законы коммутации : в цепях с реактивными элементами соблюдается принцип непрерывности во времени потокосцепления в индуктивности и электрического заряда в емкости. iL (0+ ) = iL (0−) - токи в индуктивностях не меняются скачком uC (0+ ) = uC (0− ) - напряжения на емкостях не меняются скачком Но : напряжения на индуктивностях и токи через емкости меняться скачком могут! -----------------------------------------------------------------------------------------------------Но: разумная идеализация цепи : i→∞ CU 2 CE 2 WC = = 2 2 Но: Q = CU = CE ⇒ WE = CE 2 ⇒ ∆W = WE / 2 = WRi -----------------------------------------------------------------------------------------------------Значения токов в индуктивностях и напряжений на емкостях в момент коммутации - независимые начальные условия Нулевые начальные условия ( iL (0+ ) = iL (0−) = 0 , uC (0+ ) = uC (0− ) = 0 ) - в 0+ соответствие индуктивности разрыву, емкости - перемычке Ненулевые начальные условия ⇒ в момент времени 0+ индуктивность = генератор тока i = iL (0− ) емкость = генератор напряжения e = uC (0− ) -----------------------------------------------------------------------------------------------------Пример : Дано E, R1, R2, L, C ; Определить 1) i1 i2 i3 (t=0+), 2) dii dt t =0+ 2 запасателя энергии ⇒ 2 независимых условия для уравнения 2-го порядка До коммутации ( t=0- ) : i1 (0− ) = E = i2 ( 0 − ) R1 + R2 1) i1 (0+ ) = u c ( 0− ) = 0 ⇒ и E R1 i 2 ( 0 + ) = i2 ( 0 − ) = E R1 + R2 i3 (0+ ) = i1 (0+ ) − i2 (0+ ) = E R2 R1 ( R1 + R2 ) 2) uC (0+ ) = 0 = i2 (0+ ) ⋅ R2 + L 3) i3 (0+ ) = C duC dt но E = i1 R1 + uC ; ⇒ di2 dt ⇒ t =0+ di2 dt = −E t =0+ duC i3 (0+ ) = dt C d ∗ dt ⇒ 0 = R1 di1 duC + dt dt R2 L( R1 + R2 ) duC i3 (0+ ) = , то dt C и т.к. 4) di3 dt di3 dt = t =0+ di1 dt = −E t =0 + − t =0+ di2 dt di1 dt = t =0+ = −E t =0+ R2 R ( R1 + R2 )C 2 1 − ER2 − ER2 − R ( R1 + R2 )C L( R1 + R2 ) 2 1 ⇒ 1 R2 R − 1 R1 ( R1 + R2 ) R1C L ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------Принужденный и свободный режимы 1) Составление уравнений на основе законов Кирхгофа Пример - RLC-контур (последовательный колебательный контур) di 1 Ri + L + ∫ idt = e(t ) dt C d 2) Переход к дифференциальным уравнениям ∗ dt de(t ) di d 2i 1 R +L 2 + i= dt dt C dt 3) решение - как сумма принужденного (частное) и свободного (общего) решений Y (t ) = YПРИНУЖДЕННОЕ (t ) + YСВОБОДНОЕ (t ) YПРИНУЖДЕННОЕ (t ) - поведение под воздействием вынуждающей силы (источников) YСВОБОДНОЕ (t ) - внутренние процессы системы (т.е. для нулевой правой части); выбирается из начальных условий : Y (0+ ) = YПРИНУЖДЕННОЕ (0+ ) + YСВОБОДНОЕ (0+ ) dY dt = t =0+ dYПРИНУЖДЕННОЕ dt + 0+ dYСВОБОДНОЕ dt 0+ Если воздействующая (вынуждающая) сила - постоянная или периодическая то YПРИНУЖДЕННОЕ (t ) - так же и установившееся решение Функции, описывающие YСВОБОДНОЕ (t ) называют свободными составляющими -----------------------------------------------------------------------------------------------------di d 2i 1 Пример: R + L 2 + i = 0 dt dt C Характеристическое уравнение : Lp 2 + Rp + 1 =0 C Корни p1 / 2 ; если p1 ≠ p2 , то общее решение : iСВОБОДНОЕ (t ) = A1e p1t + A2 e p2t ⇒ полное решение i (t ) = iПРИНУЖДЕННОЕ (t ) + A1e p1t + A2 e p 2 t В момент t = 0 + имеем i (0+ ) = iПРИНУЖДЕННОЕ (0) + A1 + A2 di di = ПРИНУЖДЕННОЕ dt 0+ dt + A1 p1 + A2 p2 t =0 ⇒ находятся A1 / 2 Т.о. процедура : 1) частное решение (поведение при t → ∞ ) 2) n корней характеристического уравнения p1 ... pn 3) постоянные интегрирования A1 ... An (из 1,2 и начальных условий) Переходной процесс (полное решение) : i (t ) = iПРИНУЖДЕННОЕ (t ) + A1e p1t + A2 e p2t + ... + An e pnt ----------------------------------------------------------------------------------------------------Простейшие цепи. 1) RL-цепь e(t ) = Ri + L di dt R + Lp = 0 ⇒ iСВОБОДНЫЙ (t ) = Ae R − t L ⇒ p1 = − R L i (t ) = iПРИНУЖДЕННЫЙ (t ) + Ae , R − t L i ПРИНУЖДЕННЫЙ (t ) - зависит от e(t ) а) постоянный ток e(t ) = E = const (t ) : E i ПРИНУЖДЕННЫЙ (t ) = R т.к. R − t E ⇒ i (t ) = + Ae L R i ( 0+ ) = i ( 0− ) = 0 ⇒ A=− − t E E −t i (t ) = 1 − e L = 1 − e τ , R R R E R τ= L R б) отключение (замыкание) источника : e(t < 0) = E , e(t > 0) = 0 ⇒ iПРИНУЖДЕННЫЙ (t ) = 0 , i (t > 0) = 0 + Ae i ( 0+ ) = i ( 0− ) = E R ⇒ A= E R ⇒ i (t ) = E − tτ e R R − t L в) синусоидальная (после t=0) ЭДС : e(t < 0) = 0 , e(t > 0) = Em sin(ωt + ψ ) i ПРИНУЖДЕННЫЙ = I m sin(ωt + ψ − ϕ ) принужденное решение Im = ⇒ Em R + (ωL) i (t ) = I m sin(ωt + ψ − ϕ ) + Ae i ( 0+ ) = i ( 0− ) = 0 ⇒ 2 −t τ 2 , τ = , ϕ = arctg ωL R L R A = − I m sin(ψ − ϕ ) i (t ) = I m [sin(ωt + ψ − ϕ ) − sin(ψ − ϕ ) ⋅ e −t τ ] Важный случай: ψ = ϕ - в момент коммутации iПРИНУЖДЕННЫЙ (0) = 0 = i (0−) ⇒ нет переходного процесса - сразу установившийся режим -----------------------------------------------------------------------------------------------------Для RC-цепи : постоянный ток e(t ) = E uC (t ) = E + Ae − t τ ⇒ uC _ ПРИНУЖДЕННЫЙ = E , τ = RC A = − E , т.к. uC (0+ ) = uC (0−) = 0 - все похоже на RL-цепь ⇒ −t uC = E 1 − e τ -----------------------------------------------------------------------------------------------------RC и RL цепи как интегрирующие и дифференцирующие звенья 1) интегрирующее RC звено ("интегрирующая RC-цепочка") u ВХ (t ) = RC duC du + uC ; если uC << u ВХ (t ) , то u ВХ (t ) ≈ RC C dt dt ⇒ 1 u ВХ (t )dt - т.н. интегрирующее звено; RC ∫ "забывает" интеграл на временах > τ = RC ⇒ для более медленных сигналов прямое прохождение u ВЫХ (t ) = uC ≈ 2) дифференцирующее RC звено ("дифференцирующая RC-цепочка") i =C duC dt если RC i =C и uВХ (t ) = RC duC + uC dt duC << uВХ (t ) , то uC ≈ u ВХ (t ) ⇒ dt duC du (t ) ≈ C ВХ dt dt ⇒ uВЫХ (t ) ≈ RC duВХ (t ) dt - дифференцирующее звено; чем меньше RC , тем лучше дифференцирование на временах, меньших τ = RC , дифференцирования нет (прямое прохождение) -----------------------------------------------------------------------------------------------------Аналогично - для RL -цепей : uВЫХ (t ) ≈ uВЫХ (t ) ≈ R L uВХ (t )dt при t < τ = ∫ L R L duВХ (t ) R dt при t > τ = L R