Домашнее задание № 3.1 Определить значения всех токов и
реклама
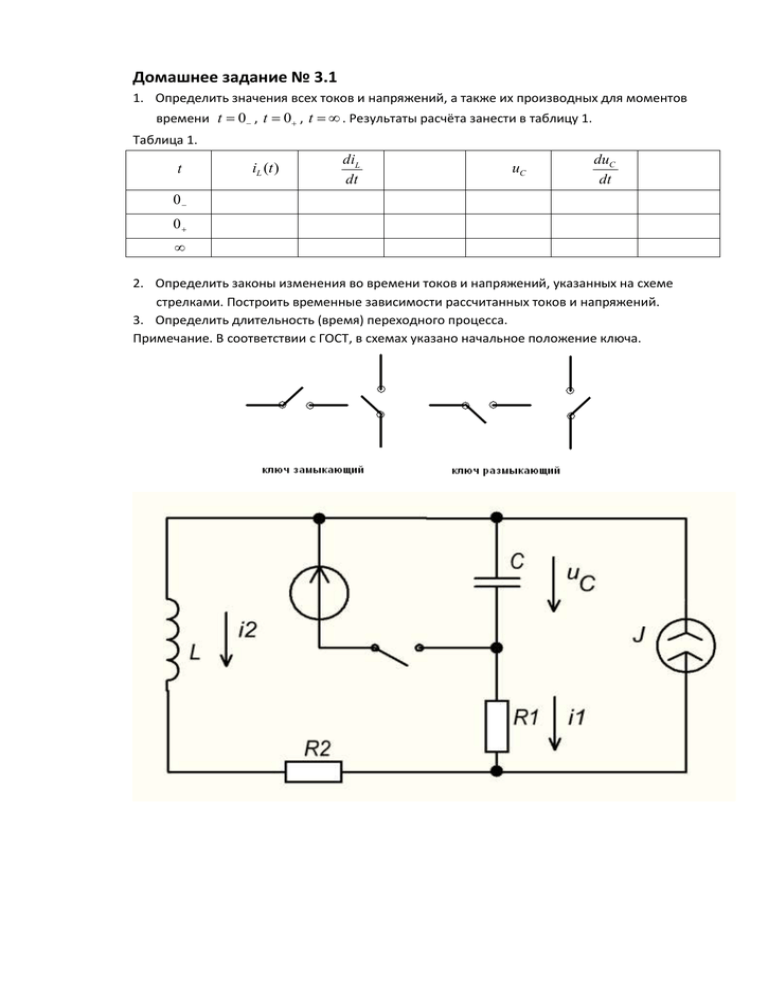
Домашнее задание № 3.1 1. Определить значения всех токов и напряжений, а также их производных для моментов времени t 0 , t 0 , t . Результаты расчёта занести в таблицу 1. Таблица 1. t iL (t ) diL dt uC duC dt 0 0 2. Определить законы изменения во времени токов и напряжений, указанных на схеме стрелками. Построить временные зависимости рассчитанных токов и напряжений. 3. Определить длительность (время) переходного процесса. Примечание. В соответствии с ГОСТ, в схемах указано начальное положение ключа. E 180 В J 1А R1 20 Ом R2 30 Ом L 0.05 Гн С 4 105 Ф 1. Определение значений токов и напряжений непосредственно до коммутации. До коммутации ключ замкнут. Поэтому по первому закону Кирхгофа: i1 (0 ) i2 (0 ) J 0 По второму закону Кирхгофа имеем для левого контура: i2 (0 ) R2 i1 (0 ) R1 E Решая совместно эти два уравнения, получим: i1 (0 ) 3 А i2 (0 ) 4 А Напряжение на конденсаторе до коммутации равняется напряжению источника ЭДС: uC (0 ) E 180 В Напряжение на индуктивности до коммутации равняется нулю uL (0 ) 0 В , так как сопротивление индуктивности постоянному току равняется нулю. Напряжения на резисторах равняются: uR1 (0 ) i1 (0 ) R1 (3) 20 60 В uR2 (0 ) i2 (0 ) R2 4 30 120 В До коммутации имеет место установившийся процесс, в котором iL i2 const и uC const , поэтому: diL 0 dt 0 duC 0 dt 0 2. Определение токов и напряжений непосредственно после коммутации. После коммутации ключ разомкнут. Согласно законам коммутации ток через индуктивность и напряжение на конденсаторе не могут измениться скачком, поэтому сразу после коммутации они равняются их значениям до неё: iL (0 ) i2 (0 ) 4 А uC (0 ) uC (0 ) E 180 В Согласно первому закону Кирхгофа, имеем: i1 (0 ) J i2 (0 ) 3 А По второму закону Кирхгофа для контура, образованного первой и второй ветвями: uL (0 ) i2 (0 ) R2 i1 (0 ) R1 uC (0 ) 0 Откуда: uL (0 ) 3 20 180 4 30 0 В diL di2 L , тогда: dt 0 dt 0 Но так как u L (0 ) L di2 0 dt 0 Так как сразу после коммутации ток через конденсатор равняется i1 (0 ) 3 А , тогда i (0 ) 3 du du i1 (0 ) С C C 1 7.5 104 В 5 с dt dt С 4 10 0 0 Так как токи не изменились сразу после коммутации, то напряжения на резисторах такие же: uR1 (0 ) i1 (0 ) R1 3 20 60 В uR2 (0 ) i2 (0 ) R2 4 30 120 В 3. Установившийся режим после коммутации ( t ). В установившемся режиме сопротивление индуктивности постоянному току равняется нулю (поэтому uL () 0 В ), а сопротивление конденсатора постоянному току равняется бесконечности, поэтому ток в первой ветви равен нулю: i1 () 0 А Тогда ток во второй ветви равняется току источника: i2 () J 1 А И напряжение на резисторе R1 равняется нулю: u R1 () 0 B Напряжение на резисторе R2 равняется: uR2 () i2 () R2 1 30 30 В Для левого контура по второму закону Кирхгофа и установившегося процесса имеем: uC () i1 () R1 i2 () R2 0 Но так как ток i1 () 0 А , то: uC () i2 () R2 30 В Составим таблицу: t iL (t ) i2 (t ) 0 4А diL dt 0А 0 4А 0А 1А 0А с с с duC dt 0В с u R1 (t ) uR2 (t ) uC (t ) 60 В 120 В 180 В 60 В 120 В 180 В 7.5 104 В 0В 30 В 30 В 0В По законам Кирхгофа для послекоммутационного режима: i1 i2 J di 1 i1dt i1R1 i2 R2 L 2 0 C dt Для свободных составляющих токов: с iC (t ) i1 (t ) 0А с 3 А 0А i1св i2св 0 di 1 i1св dt i1св R1 L 2св i2св R2 0 C dt Поэтому характеристическое уравнение имеет вид: 1 1 1 R1 pC Lp R2 0 Или после нахождения определителя и приведения к общему знаменателю: LCp 2 ( R1 R2 )Cp 1 0 pC Его корни равняются: ( R1 R2 )C ( R1 R2 ) 2 C 2 4 LC p1,2 2 LC Подставляя числовые значения, получим: p1 50 4 105 2.5 103 16 1010 4 0.05 4 105 500 500 j 2 0.05 4 105 p2 50 4 105 2.5 103 16 1010 4 0.05 4 105 500 500 j 2 0.05 4 105 Корни характеристического уравнения комплексно-сопряжённые вида p1,2 j0 , поэтому свободная составляющая тока i2 имеют вид: i2 св (t ) A2 e 500t sin(500t 2 ) Его производная: di2 св 500 A2 e 500t sin(500t 2 ) 500 A2e 500t cos(500t 2 ) dt Ток i2 равняется сумме свободной и принуждённой составляющих: i2 (t ) i2св (t ) i2 пр (t ) Принуждённая составляющая обусловлена источниками в схеме, поэтому принуждённая составляющая токов равняется: i2 пр (t ) i2 () 1 А Найдём значения свободной составляющей тока i2 в момент после коммутации t 0 : i2 св (0 ) i2 (0 ) i2 пр (0 ) 4 1 3 А Таким образом, получим первое уравнения для нахождения A2 и 2 : i2св (0 ) A2 sin 2 3 Первая производная от свободной составляющей тока i2 , учитывая, что принуждённая составляющая тока i2 пр (t ) 1 А const , в момент времени t 0 равняется: di2 св dt t 0 di2 dt 0А t 0 с Таким образом, получим второе уравнение: di2 св dt 500 A2 sin 2 500 A2 cos 2 0 t 0 Решим совместно систему уравнений: A2 sin 2 3 500 A2 sin 2 500 A2 cos 2 0 чтобы найти A2 и 2 . Отсюда получим: tg 2 1 2 450 И A2 3 3 2 4.243 А . sin 450 Значит, свободная составляющая тока i2 равняется: i2 св (t ) 4.243 e 500t sin(500t 450 ) Полный ток i2 равняется: i2 (t ) i2св (t ) i2 пр (t ) 3 2 e500t sin(500t 450 ) 1 4.243 e500t sin(500t 450 ) 1 Напряжение на конденсаторе тоже состоит из свободной и принуждённой составляющей: uС (t ) uСсв (t ) uСпр (t ) Свободная составляющая напряжения на конденсаторе имеет вид: uСсв (t ) Ae 500t sin(500t ) Найдём значение свободной составляющей напряжения на конденсаторе в момент времени t 0 : uС (0 ) 180 В Таким образом: uСсв (0 ) uС (0 ) uСпр (0 ) 180 30 150 В Так как производная от принуждённой составляющей напряжения на конденсаторе по времени равна нулю (так как uСпр (t ) 30 В const ), первая производная от свободной составляющей в момент времени t 0 равняется: duCсв dt 7.5 104 В t 0 с Первая производная имеет вид: duC 500 Ae 500t sin(500t ) 500 Ae 500t cos(500t ) dt duC 500 A sin 500 A cos dt t 0 Таким образом, воспользовавшись начальными условиями, получим 2 уравнения: A sin 150 500 A sin 500 A cos 7.5 104 Из этих уравнений найдём: arccos(0) 900 A 150 В Таким образом, свободная составляющая напряжения на конденсаторе имеет вид: uСсв (t ) 150e 500t sin(500t 900 ) И напряжение на конденсаторе: uС (t ) uСсв (t ) uСпр (t ) 150e500t sin(500t 900 ) 30 График uС (t ) : Найдём ток i1 : duC 4 105 150 (500) e 500t sin(500t 900 ) 3e 500t sin(500t 90 0 ) dt График i2 (t ) : i1 (t ) C Постоянная времени цепи: 2 0 2 0.013 с 500 Практическая длительность переходного процесса (4...5) , то есть порядка 0.065с . Ответ: t iL (t ) i2 (t ) 0 4А diL dt 0А 0 4А 0А 1А 0А с с с duC dt 0В с u R1 (t ) uR2 (t ) uC (t ) 60 В 120 В 180 В 60 В 120 В 180 В 7.5 104 В 0В 30 В 30 В 0В i1 (t ) 3e 500t sin(500t 900 ) i2 (t ) 4.243 e 500t sin(500t 450 ) 1 uС (t ) 150e500t sin(500t 900 ) 30 Длительность переходного процесса (4...5) , то есть порядка 0.065с с iC (t ) i1 (t ) 0А с 3 А 0А





