1) выполнить кинематический анализ; 2. Расчет плоских рам Вариант 36

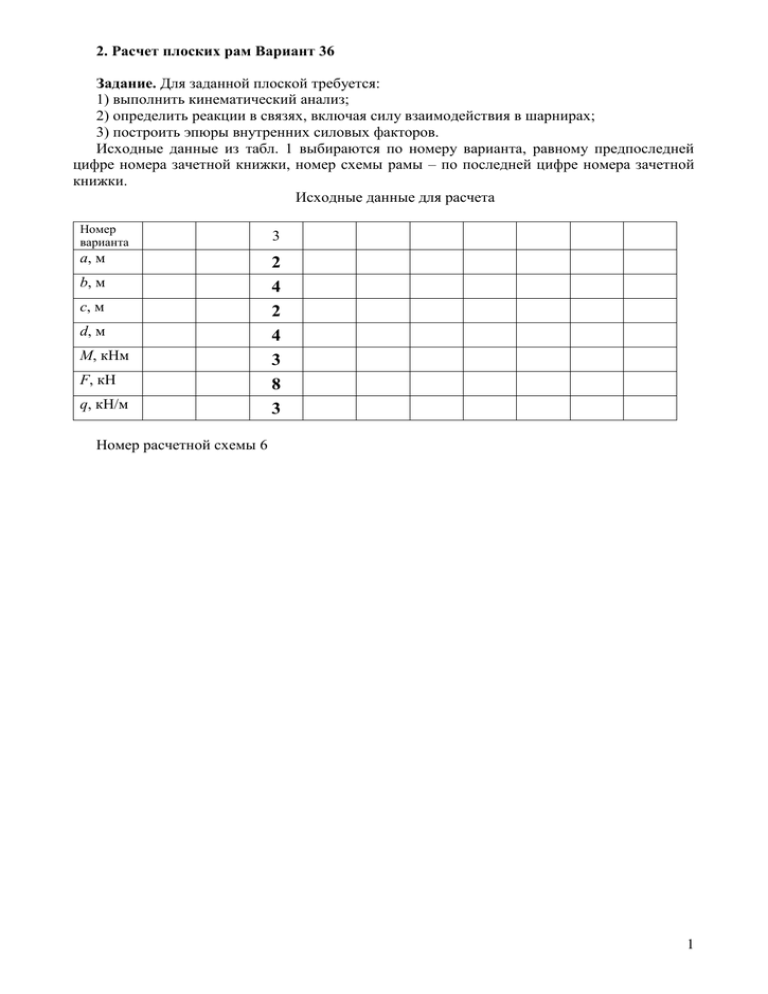
2. Расчет плоских рам Вариант 36
Задание. Для заданной плоской требуется:
1) выполнить кинематический анализ;
2) определить реакции в связях, включая силу взаимодействия в шарнирах;
3) построить эпюры внутренних силовых факторов.
Исходные данные из табл. 1 выбираются по номеру варианта, равному предпоследней
цифре номера зачетной книжки, номер схемы рамы – по последней цифре номера зачетной
книжки.
Исходные данные для расчета
Номер
варианта
a, м
b, м
c, м
d, м
M, кНм
F, кН
q, кН/м
3
2
4
2
4
3
8
3
Номер расчетной схемы 6
1
Рис. 4. Расчетные схемы статически определимых рам
2
Пример выполнения задания.
Расчетная схема к примеру показана на рис. 5. Исходные данные: Исходные данные a = 3
м, b = 2 м, c = 3 м, F = 5 кН, M = 10 кНм.
Рис. 5. Схема рамы к примеру расчета
1. Выполним кинематический анализ рамы. Кинематический анализ производится с
целью показать, что рассматриваемая рамная конструкция является статически определимой
и геометрически неизменяемой. С этой целью определяется степень свободы системы (для
статически определимых систем должна быть равна нулю). Для анализа геометрической
неизменяемости системы необходимо представить раму как совокупность простейших
геометрически неизменяемых систем (три диска, соединенные не лежащей на одной прямой
простыми шарнирами или два диска, соединенные тремя не параллельными и не
пересекающимися в одной точке связями). При этом земля рассматривается как
неизменяемый и неподвижный диск.
Степень свободы системы
W  3D  (2 Ш  С )  3  3  (2  2  5)  0.
Здесь D = 3 – число дисков (стержней без шарниров), Ш = 2 – число шарниров,
соединяющих стержни, С – число связей (3 связи – жесткая заделка, 2 связи – шарнирнонеподвижная опора).
Рама представляет собой систему из трех дисков, соединенных между собой шарнирами,
не лежащими на одной прямой (рис.6).
Рис. 6. Кинематический анализ рамы
Таким образом, геометрическая неизменяемость системы обеспечена.
3
2. Определим реакции в связях. Разъединим диски рамы, заменив шарниры и опоры
неизвестными усилиями. Из условий равновесия определим эти усилия.
Рис. 7. Определение усилий в шарнирах и реакций опор
Неизвестные усилия, заменяющие шарниры, должными быть приложены к соседним
дискам с разными знаками, внешняя сила, приложенная к шарниру, прикладываются к
любому из соседних дисков.
Записывая для дисков уравнения равновесия, получаем:
диск 1
X1  X A  5,
-
Y1  YA  10,
5 X1  2Y1  45,
- диск 2
X1  X 2 ,
Y1  Y2 ,
3 X 1  6Y1  10,
- диск 3
Y2  YB ,
X2  XB,
2X 2  M B.
Из шестого уравнения выражаем Х1 и подставляем в третье:
X1  10 / 3  2Y1 ,
45  50 / 3
50 / 3  12Y1  45  Y1 
 2,36 (кН) .
12
Определить остальные усилия не вызывает затруднений:
X 1  10 / 3  2  2.36  8, 05(кН),
YA  10  2,36  7, 64 (кН),
X A  5  8, 05  3, 05(кН),
X 2  X B  8, 05(кН),
Y2  YB  2,36 (кН),
M B  2  8, 05  16,1(кН  м).
4
Вычисленные усилия показаны на рис. 7.
Рис. 7. Направления и величины реакций
3. По найденным значениям строим эпюры продольных сил N, поперечных сил Q и
изгибающих моментов M.
а
б
в
Рис. 8. Эпюры продольных сил (а), поперечных сил (б), изгибающих моментов (в)
5
4. Проверяем равновесие жестких узлов C и D.
Рис. 9. Проверка равновесия узлов C и D.
Сумма проекций всех сил на горизонталь
– узел С
5  3, 05  8, 05  0;
– узел D
8, 05  8, 05  0.
Сумма проекций всех сил на вертикаль
– узел С
7, 62  2,36  10  0;
– узел D
2,36  2,36  0.
 FX
 FY
Сумма моментов  M
– узел С
15, 25  15, 25  0;
– узел D
24,15  10  14,15  0.
6