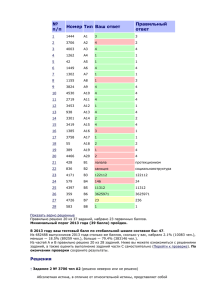
Объем одного шара в 2197 раз больше объема второго. Во... щадь поверхности первого шара больше площади поверхности второго?

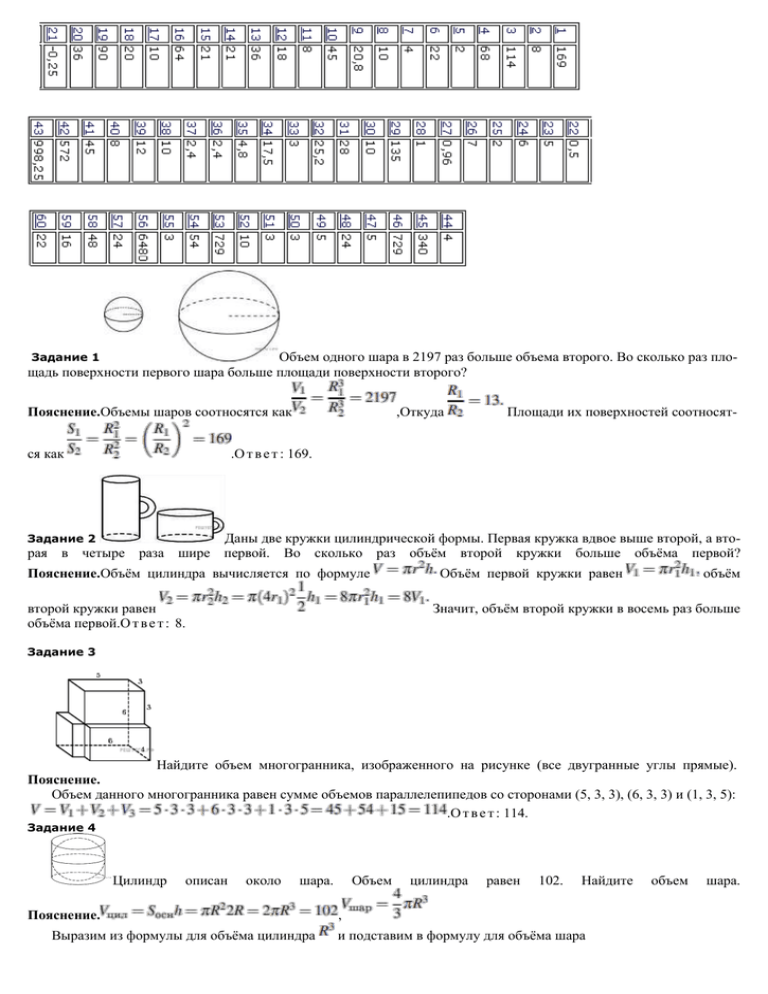
Задание 1
Объем одного шара в 2197 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Пояснение.Объемы шаров соотносятся как
ся как
,Откуда
Площади их поверхностей соотносят-
.О т в е т : 169.
Даны две кружки цилиндрической формы. Первая кружка вдвое выше второй, а вторая в четыре раза шире первой. Во сколько раз объём второй кружки больше объёма первой?
Задание 2
Пояснение.Объём цилиндра вычисляется по формуле
второй кружки равен
объёма первой.О т в е т : 8.
Объём первой кружки равен
объём
Значит, объём второй кружки в восемь раз больше
Задание 3
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Пояснение.
Объем данного многогранника равен сумме объемов параллелепипедов со сторонами (5, 3, 3), (6, 3, 3) и (1, 3, 5):
.О т в е т : 114.
Задание 4
Цилиндр
описан
около
шара.
Пояснение.
Выразим из формулы для объёма цилиндра
Объем
цилиндра
равен
102.
Найдите
,
и подставим в формулу для объёма шара
объем
шара.
О т в е т : 68.
Задание 5
Площадь боковой поверхности цилиндра равна
Пояснение.
Площадь
чит,
боковой
поверхности
, а диаметр основания — 1. Найдите высоту цилиндра.
цилиндра
находится
по
формуле:
,
зна-
.ответ: 2
Задание 6Рабочие
прокладывают тоннель длиной 87 метров, ежедневно увеличивая норму прокладки на одно и то
же число метров. Известно, что за первый день рабочие проложили 7 метров туннеля. Определите, сколько метров
туннеля проложили рабочие в последний день, если вся работа была выполнена за 6 дней.
Пояснение.Пусть рабочие в первый день проложили метров тоннеля, во второй — , …, в последний — метров
тоннеля.
Длина
имеем:
тоннеля.О т в е т : 22.
тоннеля
метров,
причем
,
где
дней.
Тогда
Следовательно, в последний день рабочие проложили 22 метра
Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?
Пояснение.Объемы подобных тел относятся как куб коэффициента подобия, поэтому один из кубов в 2 раза больше
другого. Площади поверхностей подобных тел относятся как квадрат коэффициента подобия, поэтому их отношение
равно 4.О т в е т : 4
Задание 8 Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно
70 км. На следующий день он отправился обратно в A со скоростью на 3 км/ч больше прежней. По дороге он сделал
остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь
из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч.
Пояснение.Пусть км/ч – скорость велосипедиста на пути из B в A, тогда скорость велосипедиста на пути
из A в B равна
км/ч. Сделав на обратном пути остановку на 3 часа, велосипедист затратил на обратный путь
столько же времени, сколько на путь из Aв B, отсюда
Задание 7
имеем:
Таким образом, скорость велосипедиста была равна 10 км/ч.О т в е т : 10.
Задание 9
Пирамида Снофру имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 220 м, а высота — 104 м. Сторона основания точной музейной копии этой пирамиды равна 44 см. Найдите
высоту музейной копии. Ответ дайте в сантиметрах.
Пояснение.Переведём сантиметры в метры и найдём во сколько раз сторона основания пирамиды отличается от музейной копии:
Найдём высоту музейной копии:
Задание 10
О т в е т : 20,8.
Найдите угол
многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.
Пояснение.
— квадрат со стороной 3, а
моугольный и равнобедренный,
. Поэтому угол
О т в е т : 45.
— его диагональ. Значит, треугольник
равен
— пря-
Ваш ответ: нет ответа. Правильный ответ: 45
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 11 № 500911 тип B13 (решено неверно или не решено)
Площадь боковой поверхности цилиндра равна
Пояснение.
Поскольку
а диаметр основания равен 5. Найдите высоту цилиндра.
имеем:
О т в е т : 8.
Ваш ответ: нет ответа. Правильный ответ: 8
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 12 № 77154 тип B13 (решено неверно или не решено)
Найдите объем параллелепипеда
пирамиды
равен
угольной
Пояснение.
Объем параллелепипеда
равен
,
где
–
площадь
основания,
, если объем тре3.
–
высота.
Объем
пирамиды
равен
, где
– площадь основания пирамиды, равная половине площади основания параллелепипеда.
Тогда объем параллелепипеда в 6 раз больше объема пирамиды
.
О т в е т : 18.
Ваш ответ: нет ответа. Правильный ответ: 18
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 13 № 245349 тип B13 (решено неверно или не решено)
Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.
Пояснение.
Объем цилиндра равен произведению площади основания ны высоту. Площадь основания цилиндра равна площади большого круга вписанного шара, а высота цилиндра равна диаметру вписанного шара. Поэтому
О т в е т : 36.
Ваш ответ: нет ответа. Правильный ответ: 36
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 14 № 118583 тип B13 (решено неверно или не решено)
Игорь и Паша красят забор за 24 часа. Паша и Володя красят этот же забор за 28 часов, а Володя и Игорь — за
56 часов. За сколько часов мальчики покрасят забор, работая втроем?
Пояснение.
За один час Игорь и Паша красят забор 1/24 забора, Паша и Володя красят 1/28 забора, а Володя и Игорь — 1/56
забора. Работая вместе, за один час два Игоря, Паши и Володи покрасили бы:
забора.
Тогда весь забор они покрасят за
часов.
Тем самым, они могли бы покрасить один забор за 10,5 часов. Поскольку каждый из мальчиков был учтен два
раза, в реальности Игорь, Паша и Володя могут покрасить забор за 21 час.
Ваш ответ: нет ответа. Правильный ответ: 21
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 15 № 39795 тип B13 (решено неверно или не решено)
Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит
эту работу первый рабочий, если он за 3 дня выполняет такую же часть работы, какую второй — за 4 дня?
Пояснение.
Обозначим и — объёмы работ, которые выполняют за день первый и второй рабочий, соответственно, полный объём работ примем за 1. Тогда по условию задачи
и
. Решим полученную систему:
Тем самым, первый рабочий за день выполняет одну двадцать первую всей работы, значит, работая отдельно, он
справится с ней за 21 день.
О т в е т : 21.
Ваш ответ: нет ответа. Правильный ответ: 21
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 16 № 505443 тип B13 (решено неверно или не решено)
Даны два шара. Диаметр первого шара в 8 раз больше диаметра
второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?
Пояснение.
Площади поверхностей шаров относятся как квадраты их радиусов, поэтому:
.
О т в е т : 64.
Ваш ответ: нет ответа. Правильный ответ: 64
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 17 № 107981 тип B13 (решено неверно или не решено)
Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены.
Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за
19100
рублей,
через
два
года
был
продан
за
15471 рубль.
Пояснение.
Пусть цена холодильника ежегодно снижалась на
на
процентов в год. Тогда за два года она снизилась
, откуда имеем:
Таким образом, цена холодильника ежегодно уменьшалась на 10%.
О т в е т : 10.
Ваш ответ: нет ответа. Правильный ответ: 10
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 18 № 26596 тип B13 (решено неверно или не решено)
Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит
эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй – за три дня?
Пояснение.
Обозначим и – объёмы работ, которые выполняют за день первый и второй рабочий, соответственно, полный объём работ примем за 1. Тогда по условию задачи
и
. Решим полученную систему:
Тем самым, первый рабочий за день выполняет одну двадцатую всей работы, значит, работая отдельно, он справится с ней за 20 дней.
О т в е т : 20.
Ваш ответ: нет ответа. Правильный ответ: 20
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 19 № 27192 тип B13 (решено неверно или не решено)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Пояснение.
Объем данного многогранника равен разнице объемов параллелепипедов со сторонами 5, 5, 4 и 1, 2, 5:
.
О т в е т : 90.
Ваш ответ: нет ответа. Правильный ответ: 90
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 20 № 27191 тип B13 (решено неверно или не решено)
Найдите объем многогранника, изображенного на рисунке (все двугранные углы
прямые).
Пояснение.
Объем данного многогранника равен разности объемов параллелепипедов со сторонами 5, 2, 4 и 1, 2, 2:
.
О т в е т : 36.
Задание 21
В треугольнике
угол
равен 90°,
. Найдите тангенс внешнего угла при
вершине .
Пояснение.так
как
Ответ:
,
.
Задание 22
В
треугольнике
,
Пояснение.Треугольник
прямоугольный, поэтому
нобедренный, углы при его основании равны. Поэтому
–
высота,
.
Найдите
. Треугольник
.
рав-
Ответ: 0,5.
Задание 23
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1
см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Пояснение.
Площадь четырехугольника равна сумме площадей двух прямоугольных треугольников и площади
трапеции. Поэтому
.ответ: 5
На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 2. Найдите площадь заштрихованной фигуры.
Задание 24
Пояснение.
Площади кругов относятся как квадраты их радиусов. Радиус внешнего круга равен 6, радиус внутреннего равен
3. Поскольку радиус большего круга вдвое больше радиуса меньшего круга, площадь большего круга вчетверо больше площади меньшего. Следовательно, она равна 8. Площадь заштрихованной фигуры равна разности площадей
кругов: 8 − 2 = 6.О т в е т : 6.
Задание 25
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1
см (см. рис.). Ответ дайте в квадратных сантиметрах.
Пояснение.
Площадь треугольника равна разности площади большого прямоугольника, двух прямоугольных треугольников и трапеции. Поэтому
см2.О т в е т : 2.
Примечание.
Воспользуемся формулой Пика. Площадь многоугольника, вершины которого лежат в узлах решётки, равна
Где есть количество узлов решётки внутри многоугольника, а
границе многоугольника.Тогда для данного треугольника имеем:
— количество узлов решётки на
ответ: 2
Задание
26
В
треугольнике
угол
равен
90°,
Пояснение.
.
,
Найдите
.
О т в е т : 7.
Задание 27
В
треугольнике
Пояснение.так как
имеем
угол
равен
90°,
.
Найдите
синус
внешнего
угла
при
вершине .
,
Ответ: 0,96.
Задание 28
Около окружности описан многоугольник, площадь которого равна 5. Его периметр равен 10. Найдите радиус этой окружности.
Пояснение.Радиус окружности, вписанной в многоугольник, равен отношению его площади к полупериметру. Поэтому он равен 1.О т в е т : 1.
Задание 29
Найдите градусную величину дуги
окружности, на которую опирается угол
Ответ
дайте в градусах.
Пояснение.
Дуга BC равна 90° и еще 45° (см. рис.). Всего 135°.О т в е т : 135.
Задание 30
Две стороны прямоугольника
ров
и
равны 6 и 8. Найдите длину суммы векто-
.
Пояснение.Сумма векторов
и
равна вектору
. Вектор
ных треугольника. Поэтому по теореме Пифагора
образует в прямоугольнике два прямоуголь.О т в е т : 10.
Задание 31
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Ответ дайте в квадратных сантиметрах.
1 см (см. рис.).
Пояснение.
моугольных
му
Площадь треугольника равна разности площади прямоугольника и трех прятреугольников, гипотенузы которых являются сторонами исходного треугольника.
см2.О т в е т : 28.
Задание 32
В треугольнике ABC угол C равен 90°,
Пояснение.
Углы и
,
равны как углы со взаимно перпендикулярными сторонами.
. Найдите высоту CH.
Поэто-
.
Ответ: 25,2.
Ваш ответ: нет ответа. Правильный ответ: 25,2
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 33 № 250929 тип B15 (решено неверно или не решено)
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
1 см
1 см (см. рис.). В ответе запишите
.
Пояснение.
Площадь фигуры равна трем четвертым площади круга, радиус которого равен
см. Поэтому
см2.
О т в е т : 3.
Ваш ответ: нет ответа. Правильный ответ: 3
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 34 № 250949 тип B15 (решено неверно или не решено)
Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
1 см
1 см (см. рис.). В ответе запишите
.
Пояснение.
Найдем квадрат радиуса круга
см2
Площадь фигуры равна семи восьмым площади этого круга. Поэтому
см2.
О т в е т : 17,5.
Ваш ответ: нет ответа. Правильный ответ: 17,5
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 35 № 27232 тип B15 (решено неверно или не решено)
В
треугольнике
угол
равен
90°,
.
,
Найдите
.
Пояснение.
О т в е т : 4,8.
Ваш ответ: нет ответа. Правильный ответ: 4,8
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 36 № 4787 тип B15 (решено неверно или не решено)
В треугольнике
угол
равен
,
,
. Найдите
Пояснение.
Имеем:
О т в е т : 2,4.
Ваш ответ: нет ответа. Правильный ответ: 2,4
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 37 № 30741 тип B15 (решено неверно или не решено)
.
В треугольнике ABC угол C равен 90°,
Пояснение.
Поскольку
,
. Найдите высоту CH.
имеем:
,
.
Ответ: 2,4.
Ваш ответ: нет ответа. Правильный ответ: 2,4
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 38 № 27902 тип B15 (решено неверно или не решено)
торой
Найдите диагональ прямоугольника, вписанного в окружность, радиус коравен
5.
Пояснение.
угол является прямым, он опирается на диагональ
которая является диаметром.
О т в е т : 10.
Ваш ответ: нет ответа. Правильный ответ: 10
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 39 № 27813 тип B15 (решено неверно или не решено)
Найдите
Пояснение.
В прямоугольнике диагональ делит угол в отношении
диагональ
данного
, меньшая его сторона равна 6.
прямоугольника.
диагональ делит угол в отношении
лежащего против угла в
, то есть 12.
О т в е т : 12.
, значит, углы равны
и
. Диагональ равна удвоенной длине катета,
Ваш ответ: нет ответа. Правильный ответ: 12
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 40 № 27299 тип B15 (решено неверно или не решено)
В
треугольнике
,
высота
равна
4,
.
Найдите
.
Пояснение.
.
Ответ: 8.
Ваш ответ: нет ответа. Правильный ответ: 8
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 41 № 27196 тип B16 (решено неверно или не решено)
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
.
Пояснение.
Объем данной части цилиндра равен
.
О т в е т : 45.
Ваш ответ: нет ответа. Правильный ответ: 45
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 42 № 316552 тип B16 (решено неверно или не решено)
В прямоугольном параллелепипеде
Найдите
площадь
сечения,
Пояснение.
известны длины рёбер:
проходящего
через
,
,
вершины ,
.
и .
Сечение пересекает параллельные грани по параллельным отрезкам. Поэтому сечение
грамм. Кроме того, ребро
перпендикулярно граням
и
. Поэтому углы
мые.Поэтому сечение
— прямоугольник.
Из прямоугольного треугольника
Тогда площадь прямоугольника
− параллелои
− пря-
найдем
равна:
О т в е т : 572.
Ваш ответ: нет ответа. Правильный ответ: 572
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 43 № 76809 тип B16 (решено неверно или не решено)
угол
между
боковой
гранью
Сторона основания правильной шестиугольной пирамиды равна 11, а
и
основанием
равен
45°.
Найдите
объем
пирамиды.
Пояснение.
Вершина правильной пирамиды проецируется в центр ее основания. В правильном шестиугольнике со стороной
расстояние от его центра до стороны равно радиусу вписанной окружности, который равен
как угол между боковой гранью и основанием равен 45°, высота пирамиды также равна
.
О т в е т : 998,25.
Ваш ответ: нет ответа. Правильный ответ: 998,25
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 44 № 27086 тип B16 (решено неверно или не решено)
. Так
. Тогда имеем:
объем
равен
16.
Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее
Найдите
высоту
этой
пирамиды.
Пояснение.
Объем пирамиды равен
где
– площадь основания, а
,
– высота пирамиды. Зная площадь основания, можно найти высоту:
О т в е т : 4.
Ваш ответ: нет ответа. Правильный ответ: 4
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 45 № 27069 тип B16 (решено неверно или не решено)
боковые
ребра
равны
13.
Стороны основания правильной четырехугольной пирамиды равны 10,
Найдите
площадь
поверхности
этой
пирамиды.
Пояснение.
Площадь пирамиды равна
.
Площадь боковой стороны пирамиды
ра:
. Высоту треугольника
. Тогда площадь поверхности пирамиды
.
О т в е т : 340.
Ваш ответ: нет ответа. Правильный ответ: 340
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 46 № 74429 тип B16 (решено неверно или не решено)
найдем по теореме Пифаго-
Диагональ
куба
равна
.
Найдите
его
объем.
Пояснение.
Диагональ куба в
раз больше его ребра. Поэтому ребро куба равно
Тогда объем куба
О т в е т : 729.
.
Ваш ответ: нет ответа. Правильный ответ: 729
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 47 № 500893 тип B16 (решено неверно или не решено)
Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 5 раз?
Пояснение.
Объем конуса равен
, где − площадь основания, а
раз объем конуса также уменьшится в 5 раз.
О т в е т : 5.
− высота конуса. При уменьшении высоты в 5
Ваш ответ: нет ответа. Правильный ответ: 5
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 48 № 318146 тип B16 (решено неверно или не решено)
В правильной четырёхугольной пирамиде
вания
Пояснение.
равна
.
с основанием
Найдите
боковое ребро
объём
равно 5, сторона оснопирамиды.
В основании правильной четырехугольной пирамиды лежит квадрат, вершина пирамиды проецируется в его
центр. Введем обозначения, как показано на рисунке. Диагонали квадрата перпендикулярны друг другу, треугольник
прямоугольный и равнобедренный. В нем
Тогда из прямоугольного треугольника
находим, что
Откуда для объема пирамиды имеем:
О т в е т : 24.
Ваш ответ: нет ответа. Правильный ответ: 24
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 49 № 506459 тип B16 (решено неверно или не решено)
Объём конуса равен
а его высота равна . Найдите радиус основания конуса.
Пояснение.
Найдём радиус основания конуса по формуле:
О т в е т : 5.
Ваш ответ: нет ответа. Правильный ответ: 5
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 50 № 506871 тип B16 (решено неверно или не решено)
Объём конуса равен
, а его высота равна . Найдите радиус основания конуса.
Пояснение.
Подставим числовые значения в формулу объёма
О т в е т : 3.
Ваш ответ: нет ответа. Правильный ответ: 3
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 51 № 27088 тип B16 (решено неверно или не решено)
Найдите высоту правильной треугольной пирамиды, стороны основания которой
равны
2,
а
объем
равен
.
Пояснение.
Объем пирамиды равен
где — площадь основания, а
го в основании:
,
— высота пирамиды. Найдем площадь равностороннего треугольника, лежаще-
.
Тогда высота пирамиды равна
О т в е т : 3.
Ваш ответ: нет ответа. Правильный ответ: 3
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 52 № 27163 тип B16 (решено неверно или не решено)
поверхности
Пояснение.
Из условия
которого
равна
Радиусы двух шаров равны 6, 8. Найдите радиус шара, площадь
сумме
площадей
их
поверхностей.
найдем, что радиус такого шара
.
О т в е т : 10.
Ваш ответ: нет ответа. Правильный ответ: 10
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 53 № 74847 тип B16 (решено неверно или не решено)
Найдите объем призмы, в основаниях которой лежат правильные
шестиугольники со сторонами 6, а боковые ребра равны
и наклонены к плоскости основания под углом 30 .
Пояснение.
Объем призмы
,
где — площадь основания, а — длина ребра, составляющего с основанием угол . Площадь правильного шестиугольника со стороной равна
Тогда для объема призмы имеем
.
О т в е т : 729.
Ваш ответ: нет ответа. Правильный ответ: 729
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 54 № 73703 тип B16 (решено неверно или не решено)
ный
треугольник
Пояснение.
с
катетами
3
и
6,
Основанием прямой треугольной призмы служит прямоугольбоковое ребро равно 6. Найдите объем призмы.
Объем прямой призмы равен
, где
— площадь основания, а
— ее боковое ребро. Тогда:
.
О т в е т : 54.
Ваш ответ: нет ответа. Правильный ответ: 54
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 55 № 507941 тип B16 (решено неверно или не решено)
Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 2 и 5, а второго — 5 и 6. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой
поверхности
первого?
Пояснение.
Найдём площадь поверхности первого конуса:
рого конуса:
Тогда отношение площадей:
Найдём площадь поверхности вто-
О т в е т : 3.
---------Дублирует задание 506749.
Ваш ответ: нет ответа. Правильный ответ: 3
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 56 № 73237 тип B16 (решено неверно или не решено)
вые
ребра
равны
51.
Стороны основания правильной шестиугольной пирамиды равны 48, бокоНайдите
площадь
боковой
поверхности
этой
пирамиды.
Пояснение.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. Апофему найдем по теореме Пифагора как катет прямоугольного тре-
угольника,
гипотенуза
ния:
которого
—
боковое
ребро,
а
другой
катет
—
половина
стороны
основа-
. Тогда площадь боковой поверхности
О т в е т : 6480.
Ваш ответ: нет ответа. Правильный ответ: 6480
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 57 № 501705 тип B16 (решено неверно или не решено)
Найдите объём многогранника, вершинами которого являются точки
мы
площадь
основания
которой
равна
9,
а
правильной треугольной призбоковое
ребро
равно 8.
Пояснение.
Требуется найти объём пирамиды, основание и высота которой совпадают с основанием и высотой данной треугольной призмы. Поэтому
О т в е т : 24.
Ваш ответ: нет ответа. Правильный ответ: 24
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 58 № 27110 тип B16 (решено неверно или не решено)
Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60 . Высота
пирамиды
равна
6.
Найдите
объем
пирамиды.
Пояснение.
Поскольку боковые грани
ке
и угол в треугольнике
Поэтому треугольник
,
и
равны
наклонены к основани. под углом
углы
— равносторонний, а его сторона связана с высотой формулой
и
в треугольни-
отку-
да
Из прямоугольного треугольника
Поскольку
находим:
— прямоугольник, его площадь равна произведения сторон:
Осталось найти объём пирамиды:
О т в е т : 48.
Ваш ответ: нет ответа. Правильный ответ: 48
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 59 № 508397 тип B16 (решено неверно или не решено)
Сторона основания правильной четырехугольной пирамиды равна 4, а боковое ребро равно
пирамиды.
Найдите объем
Пояснение.
В основании правильной четырёхугольной пирамиды лежит квадрат, его диагональ
равна
Отрезок AO равен половине диагонали квадрата т. е.
реме Пифагора имеем:
Из прямоугольного треугольника AOS по тео-
Объём пирамиды равен одной трети произведения площади основания на высоту:
О т в е т : 16.
Ваш ответ: нет ответа. Правильный ответ: 16
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 60 № 506519 тип B16 (решено неверно или не решено)
Найдите
Два ребра прямоугольного параллелепипеда равны 1 и 2, а объём параллелепипеда равен 6.
площадь
поверхности
этого
параллелепипеда.
Пояснение.
Найдём высоту параллелепипеда:
Найдём площадь поверхности параллелепипеда:
О т в е т : 22.
Ваш ответ: нет ответа. Правильный ответ: 22
Обсудить ВКонтакте
Сообщить об ошибке