114 куб. м. Какую сумму должен заплатить Алексей за холодную

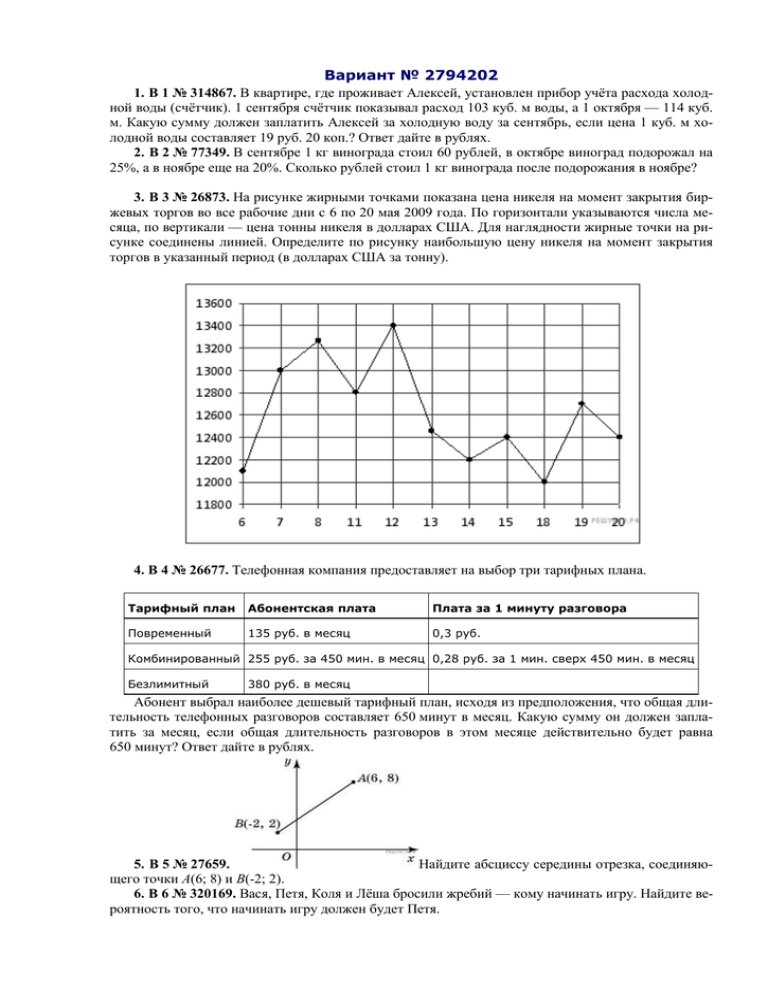
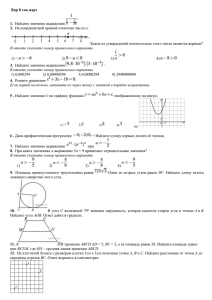
Вариант № 2794202
1. B 1 № 314867. В квартире, где проживает Алексей, установлен прибор учёта расхода холодной воды (счётчик). 1 сентября счётчик показывал расход 103 куб. м воды, а 1 октября — 114 куб.
м. Какую сумму должен заплатить Алексей за холодную воду за сентябрь, если цена 1 куб. м холодной воды составляет 19 руб. 20 коп.? Ответ дайте в рублях.
2. B 2 № 77349. В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на
25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?
3. B 3 № 26873. На рисунке жирными точками показана цена никеля на момент закрытия биржевых торгов во все рабочие дни с 6 по 20 мая 2009 года. По горизонтали указываются числа месяца, по вертикали — цена тонны никеля в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольшую цену никеля на момент закрытия
торгов в указанный период (в долларах США за тонну).
4. B 4 № 26677. Телефонная компания предоставляет на выбор три тарифных плана.
Тарифный план
Абонентская плата
Плата за 1 минуту разговора
Повременный
135 руб. в месяц
0,3 руб.
Комбинированный 255 руб. за 450 мин. в месяц 0,28 руб. за 1 мин. сверх 450 мин. в месяц
Безлимитный
380 руб. в месяц
Абонент выбрал наиболее дешевый тарифный план, исходя из предположения, что общая длительность телефонных разговоров составляет 650 минут в месяц. Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна
650 минут? Ответ дайте в рублях.
5. B 5 № 27659.
Найдите абсциссу середины отрезка, соединяющего точки A(6; 8) и B(-2; 2).
6. B 6 № 320169. Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
7. B 7 № 77382. Решите уравнение
ответе укажите меньший из них.
. Если уравнение имеет более одного корня, в
8. B 8 № 27391.
внешнего угла при вершине
В треугольнике
равен
. Найдите
угол
равен 90°, синус
.
9. B 9 № 40131.
На рисунке изображен график производной функции
. Найдите абсциссу точки, в которой касательная к графику
параллельна оси абсцисс или совпадает с ней.
10. B 10 № 928.
Площадь боковой поверхности цилиндра равна 9
, а диаметр основания равен 3. Найдите высоту цилиндра.
11. B 11 № 26786. Найдите
, если
12. B 12 № 27969. Для определения эффективной температуры звeзд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела , измеряемая в ваттах,
прямо пропорциональна площади его поверхности и четвeртой степени температуры:
где
– постоянная, площадь
измеряется в квадратных метрах, а температура
градусах Кельвина. Известно, что некоторая звезда имеет площадь
,
–в
м , а излучаемая
ею мощность не менее
Вт. Определите наименьшую возможную температуру этой
звезды. Приведите ответ в градусах Кельвина.
13. B 13 № 27097.
Во сколько раз увеличится объем шара, если его
радиус увеличить в три раза?
14. B 14 № 26592. Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1
деталь больше?
15. B 15 № 77425. Найдите наименьшее значение функции
на отрезке
.
16. C 1 № 500815. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
17. C 2 № 484577. В правильной треугольной призме
, все рёбра которой равны 1,
найдите расстояние между прямыми
и
.
18. C 3 № 500348. Решите систему неравенств:
19. C 4 № 485985. Дан прямоугольный треугольник ABC с катетами
и
С
центром в вершине B проведена окружность S радиуса 17. Найдите радиус окружности, вписанной
в уголBAC и касающейся окружности S.
20. C 5 № 484637. При каждом значении а решите систему
21. C 6 № 500197. Натуральные числа от 1 до 12 разбивают на четыре группы, в каждой из которых есть по крайней мере два числа. Для каждой группы находят сумму чисел этой группы. Для
каждой пары групп находят модуль разности найденных сумм и полученные 6 чисел складывают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Каково наименьшее возможное значение полученного результата?
Решения
↑ Задание 1 № 314867 тип B1 (решено неверно или не решено)
В квартире, где проживает Алексей, установлен прибор учёта расхода холодной воды
(счётчик). 1 сентября счётчик показывал расход 103 куб. м воды, а 1 октября — 114 куб. м. Какую
сумму должен заплатить Алексей за холодную воду за сентябрь, если цена 1 куб. м холодной воды
составляет
19
руб.
20
коп.?
Ответ
дайте
в
рублях.
Решение.
Расход воды составил 114 − 103 = 11 куб. м. Поэтому Алексей должен заплатить
11 19,2 = 211,2 руб.
О т в е т : 211,2.
Ваш ответ: нет ответа. Правильный ответ: 211,2
Гость 31.05.2013 23:45:
Скажите, ведь написано ответ дайте в рублях, так почему копейки заносятся?
Служба поддержки:
Поэтому, что двести одиннадцать целых и две десятых рубля — это и есть ответ в рублях.
Обсудить ВКонтакте Сообщить об ошибке
↑ Задание 2 № 77349 тип B2 (решено неверно или не решено)
В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%, а в ноябре
еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?
Решение.
В октябре виноград подорожал на 60 0,25 = 15 рублей и стал стоить 60 + 15 = 75 рублей. В
ноябре виноград подорожал на 75 0,2 = 15 рублей. Значит, после подорожания в ноябре 1 кг винограда стоил 75 + 15 = 90 рублей.
О т в е т : 90.
Ваш ответ: нет ответа. Правильный ответ: 90
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 3 № 26873 тип B3 (решено неверно или не решено)
На рисунке жирными точками показана цена никеля на момент закрытия биржевых торгов во
все рабочие дни с 6 по 20 мая 2009 года. По горизонтали указываются числа месяца, по вертикали — цена тонны никеля в долларах США. Для наглядности жирные точки на рисунке соединены
линией. Определите по рисунку наибольшую цену никеля на момент закрытия торгов в указанный
период (в долларах США за тонну).
Решение.
Из графика видно, что наибольшая цена одной тонны никеля составляла 13 400 долларов
США (см. рисунок).
О т в е т : 13 400.
Ваш ответ: нет ответа. Правильный ответ: 13400
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 4 № 26677 тип B4 (решено неверно или не решено)
Телефонная компания предоставляет на выбор три тарифных плана.
Тарифный план
Абонентская плата
Плата за 1 минуту разговора
Повременный
135 руб. в месяц
0,3 руб.
Комбинированный 255 руб. за 450 мин. в месяц 0,28 руб. за 1 мин. сверх 450 мин. в месяц
Безлимитный
380 руб. в месяц
Абонент выбрал наиболее дешевый тарифный план, исходя из предположения, что общая длительность телефонных разговоров составляет 650 минут в месяц. Какую сумму он должен заплатить за месяц, если общая длительность разговоров в этом месяце действительно будет равна
650 минут?
Ответ
дайте
в
рублях.
Решение.
Рассмотрим три случая.
На тарифном плане «Повременный» ежемесячная плата будет складываться из абонентской
135 руб. и платы за 650 мин. 650 0,3 = 195 руб. и будет составлять 195 + 135 = 330 руб.
На тарифном плане «Комбинированный» ежемесячная плата будет складываться из абонентской 255 руб. и платы за 200 мин. сверх тарифа 200 0,28 = 56 руб. и будет составлять
255 + 56 = 311 руб.
На тарифном плане «Безлимитный» ежемесячная плата будет равна 380 рублям.
Стоимость самого дешевого варианта составляет 311 рублей.
О т в е т : 311.
Ваш ответ: нет ответа. Правильный ответ: 311
Виктория gaidash.vika@mail.ru (Ст.Канеловская) 10.10.2013 16:28:
Почему в плане Комбинированный умножается на 200, а не на 250?
Александр Иванов (Санкт-Петербург):
650-450=200
Обсудить ВКонтакте Сообщить об ошибке
↑ Задание 5 № 27659 тип B5 (решено неверно или не решено)
8)
Найдите абсциссу середины отрезка, соединяющего точки A(6;
и B(-2;
2).
Решение.
Абсцисса середины отрезка определяется выражением:
.
О т в е т : 2.
Ваш ответ: нет ответа. Правильный ответ: 2
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 6 № 320169 тип B6 (решено неверно или не решено)
что
Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того,
начинать
игру
должен
будет
Петя.
Решение.
Жребий начать игру может выпасть каждому из четырех мальчиков. Вероятность того, что это
будет именно Петя, равна одной четвертой.
О т в е т : 0,25.
Ваш ответ: нет ответа. Правильный ответ: 0,25
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 7 № 77382 тип B7 (решено неверно или не решено)
Решите уравнение
меньший
. Если уравнение имеет более одного корня, в ответе укажите
из
них.
Решение.
На ОДЗ перейдем к уравнению на основание логарифма:
Итак, на ОДЗ уравнение имеет только один корень.
О т в е т : 12.
Ваш ответ: нет ответа. Правильный ответ: 12
Гость 03.02.2013 13:04:
Если я записал бы -2, а ответ 12, было бы ошибкой?
Служба поддержки:
Ещё какой.
Гость 27.04.2013 19:37:
Я правильно поняла, что основание логарифма не может быть отрицательным?
Служба поддержки:
Да.
Гость 31.05.2013 10:14:
В задании указано в ответе написать МЕНЬШИЙ корень. Решив квадратное уравнение, я получила два корня: −2 и 12. Поскольку −2 < 12 , в ответ должно пойти число −2.
Олег Николаевич (Петербург):
Но корень
является посторонним, так как не входит в область допустимых значений
логарифма. Логарифм
определен при
ственный корень — число 12.
Обсудить ВКонтакте Сообщить об ошибке
. Поэтому уравнение имеет един-
↑ Задание 8 № 27391 тип B8 (решено неверно или не решено)
В треугольнике
при
вершине
угол
равен
.
равен 90°, синус внешнего угла
Найдите
.
Решение.
так как
,
имеем
,
Ответ: 0,25.
Ваш ответ: нет ответа. Правильный ответ: 0,25
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 9 № 40131 тип B9 (решено неверно или не решено)
На рисунке изображен график производной функции
.
Найдите абсциссу точки, в которой касательная к графику
параллельна оси абсцисс или
совпадает
с
ней.
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку
касательная параллельна оси абсцисс или совпадает с ней, она имеет вид
, и её угловой коэффициент равен 0. Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю,
а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс. Поэтому искомая точка
.
О т в е т : -3.
Ваш ответ: нет ответа. Правильный ответ: -3
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 10 № 928 тип B10 (решено неверно или не решено)
нования
Площадь боковой поверхности цилиндра равна 9 , а диаметр ос3.
Найдите
высоту
цилиндра.
равен
Решение.
высота цилиндра равна
О т в е т : 3.
Ваш ответ: нет ответа. Правильный ответ: 3
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 11 № 26786 тип B11 (решено неверно или не решено)
Найдите
,
если
Решение.
Пользуемся периодичностью тангенса и используем формулу приведения:
О т в е т : −2,5.
Ваш ответ: нет ответа. Правильный ответ: -2,5
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 12 № 27969 тип B12 (решено неверно или не решено)
Для определения эффективной температуры звeзд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела , измеряемая в ваттах, прямо пропорциональна
площади
где
его
поверхности
– постоянная, площадь
и
четвeртой
степени
температуры:
измеряется в квадратных метрах, а температура
градусах Кельвина. Известно, что некоторая звезда имеет площадь
ею мощность
звезды.
не менее
Приведите
,
–в
м , а излучаемая
Вт. Определите наименьшую возможную температуру этой
ответ
в
градусах
Кельвина.
Решение.
Задача сводится к нахождению наименьшего решения неравенства
ном значениях постоянной
и заданной площади звезды
при извест:
О т в е т : 4000.
Ваш ответ: нет ответа. Правильный ответ: 4000
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 13 № 27097 тип B13 (решено неверно или не решено)
Во сколько раз увеличится объем шара, если его радиус увеличить
три
раза?
в
Решение.
Объем шара радиуса
равен
.
При увеличении радиуса втрое, объем шара увеличится в 27 раз.
О т в е т : 27.
Ваш ответ: нет ответа. Правильный ответ: 27
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 14 № 26592 тип B14 (решено неверно или не решено)
Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
Решение.
Обозначим — число деталей, которые изготавливает за час второй рабочий. Тогда первый
рабочий за час изготавливает
деталь. На изготовление 110 деталей первый рабочий тратит
на 1 час меньше, чем второй рабочий, отсюда имеем:
О т в е т : 10.
Ваш ответ: нет ответа. Правильный ответ: 10
Гость 02.04.2012 21:40:
Если первый рабочий тратит на час меньше, то не должно ли быть (110/n+1) - 1?
Объясните, пожалуйста, никак не сообразить
Служба поддержки:
Большее время равно увеличеному на час меньшему.
Гость 28.09.2012 15:00:
так как у второго время выполнения больше идет,то чтобы уравнять время выполнения,надо к
первой работе прибавить 1 час
Обсудить ВКонтакте Сообщить об ошибке
↑ Задание 15 № 77425 тип B15 (решено неверно или не решено)
Найдите
наименьшее
значение
функции
на
отрезке
.
Решение.
Найдем производную заданной функции:
.
Производная обращается в нуль в точках 0 и 2, заданному отрезку принадлежит число 2. Определим знаки производной функции и изобразим на рисунке поведение функции:
В точке
заданная функция имеет минимум, являющийся ее наименьшим значением на
заданном отрезке. Найдем это наименьшее значение:
.
О т в е т : −2.
Ваш ответ: нет ответа. Правильный ответ: -2
Обсудить ВКонтакте
Сообщить об ошибке
Проверка части С
Пожалуйста, оцените решения заданий части С самостоятельно, руководствуясь указанными
критериями.
Задание С1 № 500815
Критерии оценивания выполнения задания
Баллы
Обоснованно получены верные ответы в обоих пунктах
2
Обоснованно получен верный ответ в пункте а) или в пункте б)
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
2
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Решение.
а) Так как
и
, имеем:
.
Корни уравнения:
б) Корни уравнения
корни уравнения
дугой
(см. рис.).
ния:
В
— точками
указанном
изображаются точками
и , промежуток
промежутке
содержатся
и
, а
изображается жирной
три
корня
уравне-
и
О т в е т : а)
б)
Ваша оценка (баллов):
Гость 02.06.2013 16:05:
Под
а)
возможна
такая
запись
ответа:
Константин Лавров (Санкт-Петербург):
Да, возможна. Не стоит, впрочем, забывать указывать, что
Обсудить ВКонтакте Сообщить об ошибке
Задание С2 № 484577
Критерии оценивания выполнения задания
Баллы
Обоснованно получен верный ответ
2
Решение содержит обоснованный переход к планиметрической задаче, но получен
неверный ответ или решение не закончено
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
2
В правильной треугольной призме
ние между прямыми
и
.
, все рёбра которой равны 1, найдите расстоя-
Решение.
Так как прямая
пересекается с прямой
параллельной прямой
и лежит в плоскости
, параллельной
, то расстояние между прямыми
и
равно расстоянию от
прямой
до плоскости
.
Пусть АК — высота треугольника ABC. АК перпендикулярна , так как перпендикулярна плоскости ABC. Таким образом, искомое расстояние — длина отрезка АК. Из равностороннего треугольника ABC находим:
.
Ответ:
.
Ваша оценка (баллов):
Обсудить ВКонтакте
Сообщить об ошибке
Задание С3 № 500348
Критерии оценивания выполнения задания
Баллы
Обоснованно получен верный ответ
3
Обоснованно получены верные ответы в обоих неравенствах системы неравенств
2
Обоснованно получен верный ответ в одном неравенстве системы неравенств
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
3
Решите систему неравенств:
Решение.
1. Решим первое неравенство системы. Сделаем замену
Учитывая, что
получаем:
откуда находим решение первого неравенства
системы:
2. Решим второе неравенство системы:
Сделаем замену
Тогда
стемы:
3. Поскольку
или
откуда находим решение второго неравенства си-
;
получаем решение исходной системы неравенств:
Ответ:
Ваша оценка (баллов):
Обсудить ВКонтакте
Сообщить об ошибке
Задание С4 № 485985
Критерии оценивания выполнения задания
Баллы
Обоснованно получен верный ответ
3
Рассмотрена хотя бы одна возможная геометрическая конфигурация, для которой
получено правильное значение искомой величины
2
Рассмотрена хотя бы одна возможная геометрическая конфигурация, для которой
получено значение искомой величины, неправильное из-за арифметической ошибки
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
3
Дан прямоугольный треугольник ABC с катетами
и
С центром в вершине B проведена окружность S радиуса 17. Найдите радиус окружности, вписанной в угол BAC и касающейся окружности S.
Решение.
Пусть
Тогда
Пусть — радиус искомой окружности, — ее центр, — точка касания с лучом
— точка касания с окружностью
— проекция точки на прямую
Центр окружности, вписанной в угол, лежит на
его биссектрисе, значит,
Из прямоугольного треугольника
находим, что
, и тогда
Заметим, что условию задачи удовлетворяют две окружности: одна из них касается окружности внутренним образом, а вторая — внешним.
В первом случае:
По теореме Пифагора
:
откуда находим, что
Во втором случае:
Тогда
Ответ:
откуда находим, что
или
Ваша оценка (баллов):
Обсудить ВКонтакте
Сообщить об ошибке
Задание С5 № 484637
Критерии оценивания ответа на задание С5
Баллы
Обоснованно получен верный ответ.
4
Рассмотрены все возможные случаи. Получен верный ответ, но решение либо содержит пробелы, либо вычислительную ошибку или описку.
3
Рассмотрены все возможные случаи. Получен ответ, но решение содержит ошибки.
2
Рассмотрены некоторые случаи. Для рассмотренных случаев получен ответ, возможно
неверный из-за ошибок.
1
Все прочие случаи.
0
Максимальное количество баллов
4
При каждом значении а решите систему
Решение.
Пары
дающие решение системы, должны удовлетворять условиям
Из второго уравнения системы находим
.
Осталось заметить, что тогда
.
Уравнение
ние
при условиях
и
имеет при
,
реше-
.
Тогда
и из полученной системы находим
,
Ответ: при
.
решений нет, при
;
.
Ваша оценка (баллов):
Обсудить ВКонтакте
Сообщить об ошибке
Задание С6 № 500197
Критерии оценивания выполнения задания
Баллы
Верно получены все перечисленные (см. критерий на 1 балл) результаты
4
Верно получены три из перечисленных (см. критерий на 1 балл) результатов
3
Верно получены два из перечисленных (см. критерий на 1 балл) результатов
2
Верно получен один ш следующих результатов: — Обоснованное решение п. а; —
обоснованное решение п. б; — искомая оценка в п. в; — пример в п. в, обеспечивающий точность предыдущей оценки
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
4
Натуральные числа от 1 до 12 разбивают на четыре группы, в каждой из которых есть по крайней мере два числа. Для каждой группы находят сумму чисел этой группы. Для каждой пары
групп находят модуль разности найденных сумм и полученные 6 чисел складывают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Каково наименьшее возможное значение полученного результата?
Решение.
Обозначим суммы чисел в группах , , ,
парных разностей через . Можно считать, что
а) Чтобы число
а указанную в условии сумму модулей их по.
равнялось , необходимо, чтобы каждая из разностей
равнялась ,
то есть
. Сумма всех двенадцати чисел
другой стороны, она равна
, но 78 не делится на 4. Значит,
б) Чтобы число
лись . Значит,
сумм
чит,
то
равна
не равны
и число
не меньше
. Зна-
.
в) Выразим число
В
.
равнялось , необходимо, чтобы все, кроме одной, разности
равня, но в этом случае каждая из сумм ,
не равна хотя бы одной из
поэтому хотя бы три разности
,
. С
предыдущих
или
явно через
,
,
,
:
пунктах
было
показано,
что
.
Если
,
или
. В этом случае сумма всех двенадцати чисел
, то есть нечётна, что неверно.
Для следующего разбиения чисел на группы:
число равно .
;
;
;
—
Ответ: а) нет; б) нет; в) 4.
Ваша оценка (баллов):