Вариант № 2794203 1. B 1 № 26641. В университетскую

Вариант № 2794203
1. B 1 № 26641. В университетскую библиотеку привезли новые учебники по геометрии для 1–
3 курсов, по 360 штук для каждого курса. Все книги одинаковы по размеру. В книжном шкафу 9
полок, на каждой полке помещается 25 учебников. Сколько шкафов можно полностью заполнить
новыми учебниками?
2. B 2 № 26633. Клиент взял в банке кредит 12 000 рублей на год под 16%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить
всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?
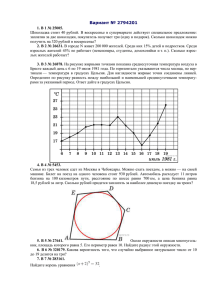
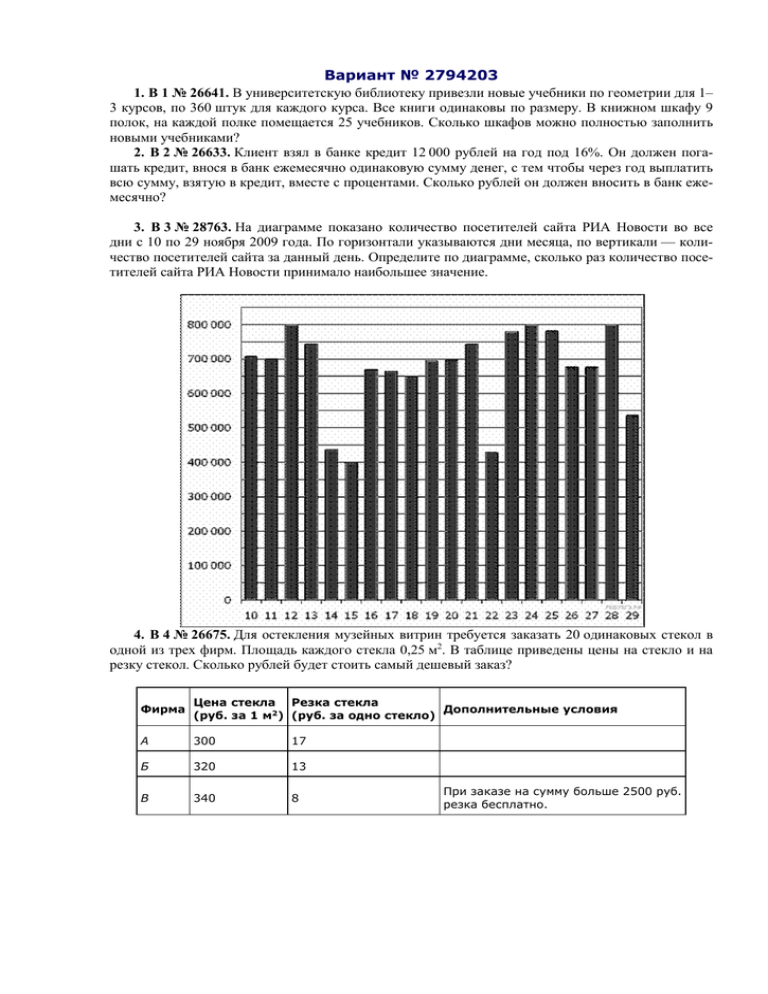
3. B 3 № 28763. На диаграмме показано количество посетителей сайта РИА Новости во все
дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день. Определите по диаграмме, сколько раз количество посетителей сайта РИА Новости принимало наибольшее значение.
4. B 4 № 26675. Для остекления музейных витрин требуется заказать 20 одинаковых стекол в
одной из трех фирм. Площадь каждого стекла 0,25 м2. В таблице приведены цены на стекло и на
резку стекол. Сколько рублей будет стоить самый дешевый заказ?
Фирма
Цена стекла Резка стекла
Дополнительные условия
(руб. за 1 м2) (руб. за одно стекло)
A
300
17
Б
320
13
В
340
8
При заказе на сумму больше 2500 руб.
резка бесплатно.
5. B 5 № 27606.
Периметр прямоугольника равен 34, а
площадь равна 60. Найдите диагональ этого прямоугольника.
6. B 6 № 285927. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается
вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете
школьнику не достанется вопроса по неравенствам.
7. B 7 № 315121. Найдите корень уравнения
8. B 8 № 27268.
,
. Найдите
9. B 9 № 122715.
В треугольнике
.
угол
равен 90°,
– высота,
.
Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите
ее скорость (в м/с) в момент времени t = 3 с.
10. B 10 № 928.
Площадь боковой поверхности цилиндра равна 9
, а диаметр основания равен 3. Найдите высоту цилиндра.
11. B 11 № 64623.
Найдите значение выражения
.
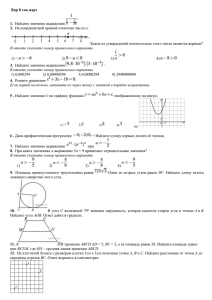
12. B 12 № 28010. Катер должен пересечь реку шириной
м и со скоростью течения
м/с так, чтобы причалить точно напротив места отправления. Он может двигаться с
разными скоростями, при этом время в пути, измеряемое в секундах, определяется выражением
, где – острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом (в градусах) нужно плыть, чтобы время в пути было не
больше 200 с?
13. B 13 № 245335.
ми которого являются точки
да
, у которого
,
,
,
,
,
,
Найдите объем многогранника, вершина,
прямоугольного параллелепипе.
14. B 14 № 99614. Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За
сколько часов выполнят заказ оба мастера, работая вместе?
15. B 15 № 245183. Найдите наименьшее значение функции
16. C 1 № 500212. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
17. C 2 № 500213. На ребре
куба
что
. Найдите угол между прямыми
и
.
.
отмечена
точка
так,
18. C 3 № 501731. Решите систему неравенств
19. C 4 № 502056. Угол C треугольника ABC равен 30°, D — отличная от A точка пересечения
окружностей, построенных на сторонах AB и AC как на диаметрах. Известно, что BD:DC = 1:6.
Найдите синус угла A.
20.
C 5 № 502078. Найдите
все
значения a,
при
которых
уравнение
имеет на промежутке
единственный корень.
21. C 6 № 500197. Натуральные числа от 1 до 12 разбивают на четыре группы, в каждой из которых есть по крайней мере два числа. Для каждой группы находят сумму чисел этой группы. Для
каждой пары групп находят модуль разности найденных сумм и полученные 6 чисел складывают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Каково наименьшее возможное значение полученного результата?
Решения
↑ Задание 1 № 26641 тип B1 (решено неверно или не решено)
В университетскую библиотеку привезли новые учебники по геометрии для 1–3 курсов, по
360 штук для каждого курса. Все книги одинаковы по размеру. В книжном шкафу 9 полок, на каждой полке помещается 25 учебников. Сколько шкафов можно полностью заполнить новыми учебниками?
Решение.
Всего привезли 360 3 = 1080 учебников по геометрии. В книжном шкафу помещается
25 9 = 225 учебников. Разделим 1080 на 225:
Значит, чтобы вместить все книги понадобится 5 шкафов, из них полностью будут заполнены
4 шкафа.
О т в е т : 4.
Ваш ответ: нет ответа. Правильный ответ: 4
Гость 28.05.2013 10:45:
их должно быть 5,т к в этой задачи остаток должен быть округлен до большего.
Петр Мурзин (Казань):
В данной задаче необходимо найти какое количество шкафов будут полностью заполнены
учебниками?" Полученный ответ округлять не нужно.
Обсудить ВКонтакте Сообщить об ошибке
↑ Задание 2 № 26633 тип B2 (решено неверно или не решено)
Клиент взял в банке кредит 12 000 рублей на год под 16%. Он должен погашать кредит, внося
в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую
в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?
Решение.
Через год клиент должен будет выплатить 12 000 + 0,16 12 000 = 13 920 рублей. Разделим
13 920 руб. на 12 мес.:
руб./мес.
Значит, клиент должен вносить ежемесячно в банк 1160 рублей.
О т в е т : 1160.
Ваш ответ: нет ответа. Правильный ответ: 1160
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 3 № 28763 тип B3 (решено неверно или не решено)
На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей
сайта за данный день. Определите по диаграмме, сколько раз количество посетителей сайта РИА
Новости принимало наибольшее значение.
Решение.
Из диаграммы видно, что посетителей сайта РИА Новости принимало наибольшее значение 3
раза (см. рисунок).
О т в е т : 3.
Ваш ответ: нет ответа. Правильный ответ: 3
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 4 № 26675 тип B4 (решено неверно или не решено)
Для остекления музейных витрин требуется заказать 20 одинаковых стекол в одной из трех
фирм. Площадь каждого стекла 0,25 м2. В таблице приведены цены на стекло и на резку стекол.
Сколько рублей будет стоить самый дешевый заказ?
Фирма
Цена стекла Резка стекла
Дополнительные условия
(руб. за 1 м2) (руб. за одно стекло)
A
300
17
Б
320
13
В
340
8
При заказе на сумму больше 2500 руб.
резка бесплатно.
Решение.
Общая площадь стекла, которого нужно изготовить равна 20 0,25 = 5 м2.
Стоимость заказа в фирме А складывается из стоимости стекла 300 5 = 1500 руб. и стоимости
его резки и шлифовки 17 20 = 340 руб. Всего 1840 руб.
Стоимость заказа в фирме Б складывается из стоимости стекла 320 5 = 1600 руб. и стоимости
его резки и шлифовки 13 20 = 260 руб. Всего 1860 руб.
Стоимость заказа в фирме В складывается из стоимости стекла 340 5 = 1700 руб. и стоимости
его резки и шлифовки 8 20 = 160 руб. Всего 1860 руб.
Стоимость самого дешевого заказа составляет 1840 рублей.
О т в е т : 1840.
Ваш ответ: нет ответа. Правильный ответ: 1840
Гость 18.12.2012 19:11:
Простите за беспокойство, объясните, пожалуйста, разве надо не лист квадрата в 1 кв. м. разрезать на 4 части? На первый взгляд кажется, что нужно купить 5 квадратных листов стекла по 1
квадратному метру и разрезать их по числу стёкол.
Служба поддержки:
Стекла (обои, линолеум, деревянные панели, другие отделочные и строительные материалы) в
виде квадратных листов обычно не производятся и не продаются. Хотя цена на эти товары
зависит от их площади в квадратных метрах.
Neon Burg (Trechtown) 09.05.2013 13:32:
Возник вопрос. Чтобы получить 20 одинаковых стекол по 0,25 кв. м, нужно разрезать 5 стекол по
1 кв. м. Следовательно, 17 рублей (резка стекла руб. за одно стекло) нужно умножать на 5
(стекол), а не на 20. И ответ тогда будет 1585 руб. Разве не так ?
Служба поддержки:
В условии не сказано, что имеются стеклянные листы размером 1х1 метр. Кроме того, из практических соображений ясно, что каждое отдельное стекло нужно после резки с каждой стороны
шлифовать. Поэтому разумна цена за обработку каждого отдельного стекла, а не за 4 разреза на
5 стекол.
Гость 25.09.2013 19:23:
А может подправите её чтобы до всех доходило? Думаю, половина делают ошибки из-за этого.
Служба поддержки:
Задача не наша, а государственная.
Обсудить ВКонтакте Сообщить об ошибке
↑ Задание 5 № 27606 тип B5 (решено неверно или не решено)
Найдите
диагональ
Периметр прямоугольника равен 34, а площадь равна 60.
этого
прямоугольника.
Решение.
Периметр прямоугольника равен сумме длин его сторон. Площадь прямоугольника равна их
произведению. Обозначим длины сторон и . Тогда периметр и площадь прямоугольника соответственно равны
и
. Решим систему:
Тем самым, стороны прямоугольника треугольника равны 5 и 12.
Диагональ разбивает прямоугольник на два прямоугольных треугольника, в которых она является гипотенузой. Пусть длина диагонали равна , тогда по теореме Пифагора
О т в е т : 13.
Примечание 1.
Можно заметить, что система уравнений
является системой Виета. Поэто-
му её решения — корни квадратного уравнения
откуда
и
.
Примечание 2.
Можно было и вовсе не решать систему уравнений: действительно,
откуда
.
Ваш ответ: нет ответа. Правильный ответ: 13
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 6 № 285927 тип B6 (решено неверно или не решено)
В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не
достанется
вопроса
по
неравенствам.
Решение.
Из 25 билетов 15 не содержат вопроса по неравенствам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна
О т в е т : 0,6.
Ваш ответ: нет ответа. Правильный ответ: 0,6
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 7 № 315121 тип B7 (решено неверно или не решено)
Найдите
корень
уравнения
Решение.
Используя формулу
О т в е т : 6.
Примечание.
, получаем:
.
Следует отличать это уравнение от похожего, но другого:
. В этом случае имеем:
Ваш ответ: нет ответа. Правильный ответ: 6
Никита Белов (Владивосток) 02.06.2013 06:21:
а у вас в примерах скобки точно не должны быть?
Олег Николаевич (Петербург):
Скобки поставлены там, где нужно.
Гость 09.09.2013 19:00:
откуда 1/2 ?
Александр Иванов (Санкт-Петербург):
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 8 № 27268 тип B8 (решено неверно или не решено)
В треугольнике
угол
равен 90°,
– высота,
,
.
.
Найдите
Решение.
.
Ответ: 17,5.
Ваш ответ: нет ответа. Правильный ответ: 17,5
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 9 № 122715 тип B9 (решено неверно или не решено)
Материальная точка движется прямолинейно по закону
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите
ее скорость (в м/с) в момент времени t = 3 с.
Решение.
Найдем закон изменения скорости:
.
Тогда находим:
м/с.
О т в е т : 8.
Ваш ответ: нет ответа. Правильный ответ: 8
Диана Малянина (Москва) 21.04.2013 13:21:
В формуле t^2 с минусом. Значит, должно быть 9.
Гость 04.05.2013 13:03:
-t^2=-3^2=9. Разве не так?
Александр Иванов (Санкт-Петербург):
не
так
,
вот
а
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 10 № 928 тип B10 (решено неверно или не решено)
нования
Площадь боковой поверхности цилиндра равна 9 , а диаметр ос3.
Найдите
высоту
цилиндра.
равен
Решение.
высота цилиндра равна
О т в е т : 3.
Ваш ответ: нет ответа. Правильный ответ: 3
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 11 № 64623 тип B11 (решено неверно или не решено)
Найдите значение выражения
.
Решение.
В силу периодичности косинуса и симметричности синуса
,
. Далее используем формулы приведения:
.
О т в е т : 0,4.
Ваш ответ: нет ответа. Правильный ответ: 0,4
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 12 № 28010 тип B12 (решено неверно или не решено)
Катер должен пересечь реку шириной
м и со скоростью течения
м/с так,
чтобы причалить точно напротив места отправления. Он может двигаться с разными скоростями,
при этом время в пути, измеряемое в секундах, определяется выражением
, где – острый угол, задающий направление его движения (отсчитывается от берега). Под каким минимальным углом
(в градусах) нужно плыть, чтобы время в пути было не больше 200 с?
Решение.
Задача сводится к решению неравенства
значениях длины реки
м и скорости течения
на интервале
м/с:
при заданных
.
О т в е т : 45.
Ваш ответ: нет ответа. Правильный ответ: 45
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 13 № 245335 тип B13 (решено неверно или не решено)
ся точки ,
го
,
Решение.
,
,
,
,
Найдите объем многогранника, вершинами которого являютпрямоугольного параллелепипеда
, у которо-
,
.
Из рисунка видно, что многогранник является половиной
данного прямоугольного параллелепипеда. Следовательно, объём искомого многогранника
О т в е т : 30.
Ваш ответ: нет ответа. Правильный ответ: 30
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 14 № 99614 тип B14 (решено неверно или не решено)
Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За сколько часов выполнят
заказ
оба
мастера,
работая
вместе?
Решение.
Первый мастер выполняет 1/12 работы в час, а второй — 1/6 работы в час. Следовательно, работая вместе, мастера выполняют
нят за 4 часа.
работы в час. Поэтому всю работу мастера выпол-
Другое рассуждение.
Время работы равно отношению объёма к скорости её выполнения. Поэтому два мастера, работая вместе, выполнят заказ за
часа.
О т в е т : 4.
Ваш ответ: нет ответа. Правильный ответ: 4
Обсудить ВКонтакте
Сообщить об ошибке
↑ Задание 15 № 245183 тип B15 (решено неверно или не решено)
Найдите наименьшее значение функции
Решение.
Поскольку функция
возрастающая, заданная функция достигает наименьшего значения
в той же точке, в которой достигает наименьшего значения выражение
Квадратный
трехчлен
с положительным старшим коэффициентом достигает наименьшего
значения в точке
в нашем случае — в точке −1. Значение функции в этой точке
равно
О т в е т : 16.
Ваш ответ: нет ответа. Правильный ответ: 16
Обсудить ВКонтакте
Сообщить об ошибке
Проверка части С
Пожалуйста, оцените решения заданий части С самостоятельно, руководствуясь
указанными критериями.
Задание С1 № 500212
Критерии оценивания выполнения задания
Баллы
Обоснованно получены верные ответы в обоих пунктах
2
Обоснованно получен верный ответ в пункте а или в пункте б
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
2
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решение.
а) Запишем уравнение в виде
.
Значит,
или
да
—
,
уравнение
не
имеет
корней,
или
,
отку-
.
б) С помощью числовой окружности отберем корни уравнения, принадлежащие отрезку
.
Получим число
Ответ: а)
.
; б)
,
.
Ваша оценка (баллов):
Обсудить ВКонтакте
Сообщить об ошибке
Задание С2 № 500213
Критерии оценивания выполнения задания
Баллы
Обоснованно получен верный ответ
2
Решение содержит обоснованный переход к планиметрической задаче, но получен
неверный ответ или решение не закончено, или при правильном ответе решение
недостаточно обосновано
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
2
На ребре
куба
угол между прямыми
Решение.
отмечена точка
и
.
так, что
. Найдите
Примем
Тогда
ребро
куба
за
.
.
Поскольку
, получаем:
и
.
Проведем через точку
прямую, параллельную
. Она пересекает ребро
в точке ,
причем треугольники
и
равны. Искомый угол равен углу
(или смежному с
ним).
В прямоугольном треугольнике
В прямоугольном треугольнике
В треугольнике
откуда
Тогда
с прямым углом
с прямым углом
Ответ
может
виде:
быть
представлен
и
в
другом
или
Ответ:
.
Ваша оценка (баллов):
Обсудить ВКонтакте
Сообщить об ошибке
Задание С3 № 501731
Критерии оценивания выполнения задания
Баллы
Обоснованно получен верный ответ
3
Обоснованно получены верные ответы в обоих неравенствах исходной системы
2
Обоснованно получен верный ответ в одном неравенстве исходной системы
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
3
Решите систему неравенств
Решение.
1. Решим первое неравенство системы:
Рассмотрим два случая. Первый случай:
откуда
Второй случай:
откуда
Решение первого неравенства исходной системы:
2. Решим второе неравенство системы:
где
где
Решение второго неравенства исходной системы:
3. Решение исходной системы неравенств:
Ответ:
Ваша оценка (баллов):
Обсудить ВКонтакте
Сообщить об ошибке
Задание С4 № 502056
Критерии оценивания выполнения задания
Баллы
Имеется верное доказательство утверждения пункта a и обоснованно получен верный
ответ в пункте б
3
Получен обоснованный ответ в пункте б ИЛИ имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за
арифметической ошибки
2
Имеется верное доказательство утверждения пункта а ИЛИ при обоснованном решении
пункта б получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно по1
лучен верный ответ в пункте б с использованием утверждения пункта а, при этом
пункт а не выполнен
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
3
Угол C треугольника ABC равен 30°, D — отличная от A точка пересечения окружностей, построенных на сторонах AB и ACкак на диаметрах. Известно, что BD:DC = 1:6. Найдите синус
угла A.
Решение.
Пусть BD = х, тогда по условию DC = 6х.
Поскольку D — точка пересечения окружностей, построенных на сторонах АВ и АС как на
диаметрах,
значит, точки B,С и D лежат на одной прямой. В прямоугольном треугольнике ACD угол
откуда
В прямоугольном треуголь-
ник ABD:
Возможны два случая. Первый случай: угол ABC тупой (рис.1), тогда точка B лежит между
точками D и C, значит
. По теореме синусов для треугольника ABC:
откуда
Второй случай: угол ABC острый (рис.2), тогда точка D лежит между точками B и С, значит,
По теореме синусов для треугольника ABC:
отку-
да
Ответ:
Ваша оценка (баллов):
Обсудить ВКонтакте
Сообщить об ошибке
Задание С5 № 502078
Критерии оценивания ответа на задание С5
Баллы
Обоснованно получен верный ответ.
4
Обоснованно получены оба значения: a=-\frac{1}{8}, \ a=0. Ответ отличается от верного исключением точки a = 0
3
Обоснованно получены оба значения: a=-\frac{1}{8}, \ a=0.
2
Верно найдено одно или два из значений a=-\frac{1}{8} или a=0.
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
Найдите все значения a, при которых уравнение
промежутке
4
имеет на
единственный корень.
Решение.
Рассмотрим два случая. Первый случай:
Исходное уравнение примет
вид
Последнее
уравнение
при
имеет
на
промежутке
откуда
ство
Подставив
получим:
В этом случае уравнение
единственный корень
ке
корней при
да
в
корень
неравен-
откуда
имеет на промежут-
при
и не имеет на промежут-
и при
Исходное уравнение примет вид
Последнее уравнение имеет на промежутке
вив
в
при условии
ке
Второй случай:
единственный
неравенство
единственный корень
получим:
Подстаотку-
В этом случае уравнение
промежутке
ке
при условии
единственный корень
при
имеет на
и не имеет на промежут-
корней при
Уравнение
на промежутке
• при
не имеет корней;
• при
имеет единственный корень
• при
• при
Ответ:
имеет два различных корня
;
и
имеет единственный корень
[0; +∞)
Ваша оценка (баллов):
Обсудить ВКонтакте
Сообщить об ошибке
Задание С6 № 500197
Критерии оценивания выполнения задания
Баллы
Верно получены все перечисленные (см. критерий на 1 балл) результаты
4
Верно получены три из перечисленных (см. критерий на 1 балл) результатов
3
Верно получены два из перечисленных (см. критерий на 1 балл) результатов
2
Верно получен один ш следующих результатов: — Обоснованное решение п. а; —
обоснованное решение п. б; — искомая оценка в п. в; — пример в п. в, обеспечивающий точность предыдущей оценки
1
Решение не соответствует ни одному из критериев, перечисленных выше
0
Максимальный балл
4
Натуральные числа от 1 до 12 разбивают на четыре группы, в каждой из которых есть по крайней мере два числа. Для каждой группы находят сумму чисел этой группы. Для каждой пары
групп находят модуль разности найденных сумм и полученные 6 чисел складывают.
а) Может ли в результате получиться 0?
б) Может ли в результате получиться 1?
в) Каково наименьшее возможное значение полученного результата?
Решение.
Обозначим суммы чисел в группах , , ,
парных разностей через . Можно считать, что
а) Чтобы число
а указанную в условии сумму модулей их по.
равнялось , необходимо, чтобы каждая из разностей
равнялась ,
то есть
. Сумма всех двенадцати чисел
другой стороны, она равна
, но 78 не делится на 4. Значит,
б) Чтобы число
лись . Значит,
сумм
чит,
то
равна
не равны
и число
не меньше
. Зна-
.
в) Выразим число
В
.
равнялось , необходимо, чтобы все, кроме одной, разности
равня, но в этом случае каждая из сумм ,
не равна хотя бы одной из
поэтому хотя бы три разности
,
. С
предыдущих
или
явно через
,
,
,
:
пунктах
было
показано,
что
.
Если
,
или
. В этом случае сумма всех двенадцати чисел
, то есть нечётна, что неверно.
Для следующего разбиения чисел на группы:
число равно .
Ответ: а) нет; б) нет; в) 4.
;
;
;
—