Простые и составные числа.
реклама

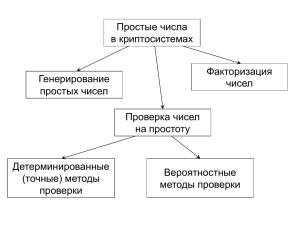
Простые и составные числа. Число - одно из основных понятий математики, позволяющее выразить результаты счета или измерения. Каждое натуральное число, больше единицы, делится, по крайней мере, на два числа: на 1 и на само себя. Если ни на какое другое натуральное число нацело не делится, то оно называется простым, а если у него имеются, еще какие-то делители, то - составным. К простым и составным не относится только 1. Небольшую «коллекцию» простых чисел нам поможет составить старинный способ, придуманный ещё в III веке до н. э. Эратосфеном, киренским хранителем знаменитой Александрийской библиотеки. Выпишем несколько подряд идущих чисел, начиная с 2. 2 отберём в свою коллекцию, а остальные числа, кратные 2, зачеркнём. Ближайшим будет 3. Его оставляем для коллекции, а все остальные числа, кратные 3, зачеркнём. При этом оказывается, что некоторые числа уже вычеркнуты раньше, например: 6, 12 и др. Следующее наименьшее незачёркнутое число – это 5. Берём 5, а кратные 5 – зачёркиваем. Повторяя эту процедуру снова и снова, мы добьёмся того, что незачёркнутыми останутся одни простые числа – они словно просеялись сквозь решето. Такой способ получил название «решето Эратосфена». А почему решето? Во времена Эратосфена писали на восковых дощечках, а вместо того, чтобы числа вычеркивать, дощечку в нужном месте прокалывали. Отсюда и название способа – «решето Эратосфена». Эратосфен Киренский— древнегреческий математик (276-194 до нашей эры), заведовал Александрийской библиотекой и заложил основы математической географии, вычислив с большой точностью величину земного шара. Первую известную нам таблицу простых чисел составил итальянский математик Пьетро Антонио Катальди в 1603 году. Она охватывала все простые числа от 2 до 743. Леонарду Эйлеру удалось доказать, что 2 147 483 647 есть простое число. Очень долго оно считалось самым большим из известных науке простых чисел, но в 1883 году Иван Михеевич Первушин сумел доказать, что 2 305 843 002 913 693 951 есть простое число. В наше время с помощью ЭВМ найдено еще несколько простых чисел, но записать их цифрами подряд трудно, в них столько цифр, что их хватит на целую книгу. Следующий, заинтересовавший математиков вопрос был о количестве простых чисел. Ответ находится в девятой книге знаменитого сочинения Евклида «Начала» - нетленного памятника древнего мира. Двадцатая теорема в этой книге утверждает: « Первых простых чисел существует больше любого указанного числа их». Вот доказательство этой теоремы. Предположим, что существует некое наибольшее простое число p. Тогда перемножим все простые числа, начиная с числа 2 и заканчивая числом p, и увеличим полученное произведение на единицу. Результат этих действий обозначим M. 2*3*5*…*P+ 1=M Если число M составное, то оно должно иметь по крайне мере один простой делитель. Но этим делителем не может быть ни одно из простых чисел 2, 3, 5, 7, … p. Поскольку при делении M на каждое из них получаем в остатке один. Следовательно, число M либо само простое, либо делится на простое число большее p. Значит предположение, что существует наибольшее простое число p, неверно и множество простых чисел бесконечно. Простые числа - это ключ к разрешению многих математических проблем, они также играют большую роль в криптографии (шифровании), благодаря чему интересуют не только математиков, но и военных, разведку и контрразведку. Таблица простых чисел есть на форзаце1 учебника математики за 6 класс. Простые числа-близнецы — пары простых чисел, отличающихся на 2. Первые простые числа-близнецы: (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), 1 Фо́рзац (нем. Vorsatz) — Элемент конструкции книги, соединяющий книжный блок с переплётной крышкой. Обычно выполняет декоративнооформительскую функцию: скрыть "изнаночную" сторону переплетной крышки и место крепления последней с книжным блоком. Часто на форзацах помещают различные справочные данные (словари, учебники).