Простые и составные числа
реклама

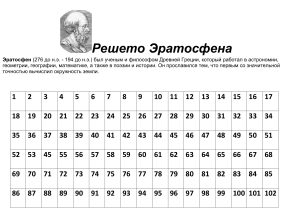
Простые и составные числа Определение Натуральное число называют простым, если оно имеет два делителя: единицу и само это число. Например: 2, 3, 5, 7, 11, 13,… Определение Натуральное число называют составным, если оно имеет более двух делителей. Например: 4, 6, 8, 9, 10, … 1 – не простое и не составное число. Любое составное число можно разложить на множители. Например: число 78 составное, потому что кроме 1 и 78, оно делится, например, еще на 2. Так как 78 : 2 = 39, то 78 = 2 · 39. Говорят , что число 78 разложено на множители. Простое число так разложить на множители нельзя Пифагор о числах Пифагор и его ученики изучали вопрос о делимости чисел. Число , равное сумме всех его делителей (без самого числа), они называли совершенным числом. Например, числа 6 (6 = 1 + 2 + 3), 28 (28 = 1 + 2 + 4 + 7 + 14) совершенные. Следующие совершенные числа 496, 8128, 33 550 336. Пифагорейцы знали только первые три совершенные числа. Совершенные числа Четвертое 8128 – стало известно в I в.н.э. Пятое – 33 550 336 – было найдено в XV в. К 1983 г. было известно уже 27 совершенных чисел. Но до сих пор ученые не знают, есть ли нечетные совершенные числа, есть ли самое большое совершенное число. Интерес древних математиков к простым числам связан с тем, что любое число простое, либо может быть представлено в виде произведения простых чисел, т.е простые числа – это как бы кирпичики, из которых строятся остальные натуральные числа. Древнегреческий математик Евклид (III в до н.э.) в своей книге «Начала», бывшей на протяжении двух тысяч лет основным учебником математики , доказал, что простых чисел бесконечно много, т.е. за каждым простым числом есть большее простое число. Греческий математик Эратосфен придумал такой способ. Он записывал все числа от 1 до какогото числа, а потом вычеркивал единицу, который не является ни простым, ни составным числом, затем вычеркивал через одно все числа, идущие после 2 (числа, кратные 2, т.е. 4,6,8 и т.д.) Решето Эратосфена 1 11 21 31 2 12 22 32 3 13 23 33 4 14 24 34 5 6 7 8 9 10 15 16 17 18 19 20 25 26 27 28 29 30 35 36 37 38 39 40 Греки делали запись на покрытых воском табличках или на натянутом папирусе, а числа не вычеркивали, а выкалывали иглой, то таблица в конце вычислений напоминало решето. Поэтому метод Эратосфена называют решетом Эратосфена: в этом решете «отсеиваются» простые числа от составных.