Работа №29 (срок сдачи 12 мая 2015) 1. Найдите значение
реклама
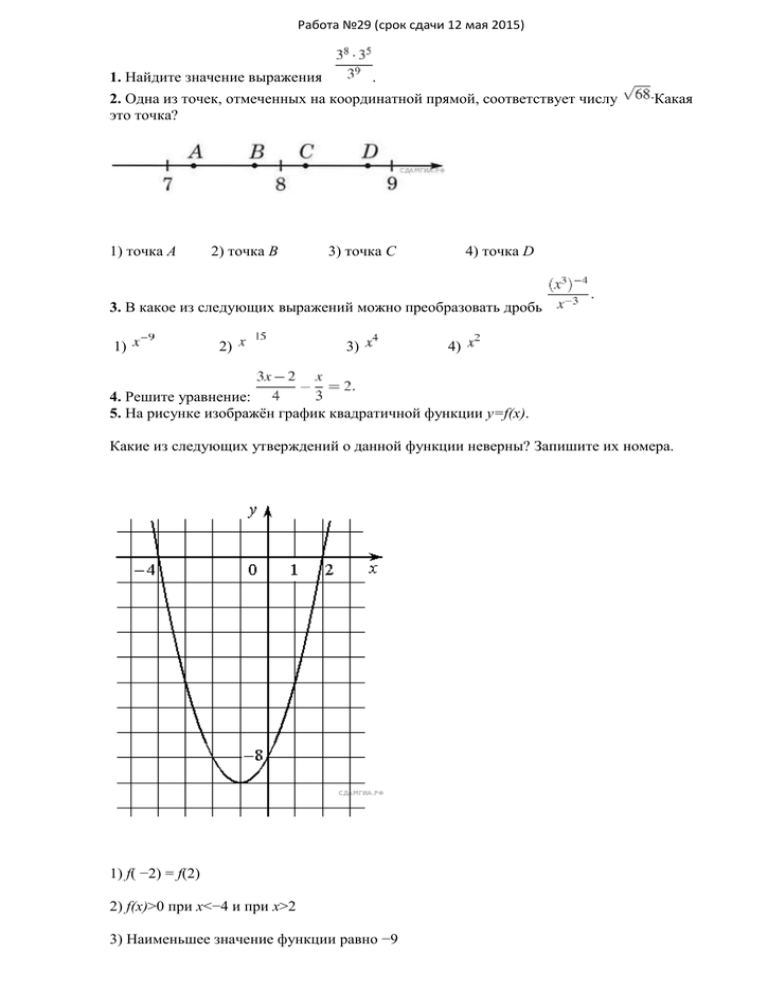
Работа №29 (срок сдачи 12 мая 2015) 1. Найдите значение выражения . 2. Одна из точек, отмеченных на координатной прямой, соответствует числу это точка? 1) точка A 2) точка B 3) точка C Какая 4) точка D 3. В какое из следующих выражений можно преобразовать дробь 1) 2) 3) 4) 4. Решите уравнение: 5. На рисунке изображён график квадратичной функции y=f(x). Какие из следующих утверждений о данной функции неверны? Запишите их номера. 1) f( −2) = f(2) 2) f(x)>0 при x<−4 и при x>2 3) Наименьшее значение функции равно −9 6. Геометрическая прогрессия задана условием членов. 7. Найдите значение выражения Найдите сумму первых её 4 при 8. На каком из рисунков изображено решение неравенства 9. Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков? 10. Боковая сторона равнобедренного треугольника равна 4. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника. 11.В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напро- тив этой диагонали, равен 45°. Найдите площадь ромба, деленную на 12. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах. 13. Какие из следующих утверждений верны? 1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны. 2) Если угол равен 60°, то смежный с ним равен 120°. 3) Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны. 4) Через любые три точки проходит не более одной прямой. 14. На диаграмме показано количество посаженных деревьев и кустарников в г. Сочи за период с 2009 по 2012 гг. Определите, сколько всего было посажено зелёных насаждений за 2011 г. и 2012 г.? 1) 10 000 2) 4 000 3) 12 000 4) 8 000 15. На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления во вторник. 16. В начале учебного года в школе было 1250 учащихся, а к концу года их стало 950. На сколько процентов уменьшилось за год число учащихся? 17. Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 3,2 м от земли. Длина троса равна 4 м. Найдите расстояние от точки основания флагштока до места крепления троса на земле. Ответ дайте в метрах. 18. Какая из следующих круговых диаграмм показывает распределение оценок по контрольной работе по математике в 8-х классах школы, если из всех оценок в классе пятёрок примерно 35%, четвёрок — примерно 25%, а троек — примерно 23%? 19. На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней. 20. Площадь треугольника можно вычислить по формуле , где — сторона треугольника, — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону равна 14 м. , если площадь треугольника равна , а высота 21. Решите уравнение 22. Задание 22 № 314493. Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 3 часа, вернулись обратно через 5 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 6 км/ч? 23. Постройте график функции и найдите все значения при которых он имеет ровно три общие точки с прямой 24. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140° . 25. В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AMB.