Лекция № 6 Математические основы статистических методов анализа качества изделий
реклама
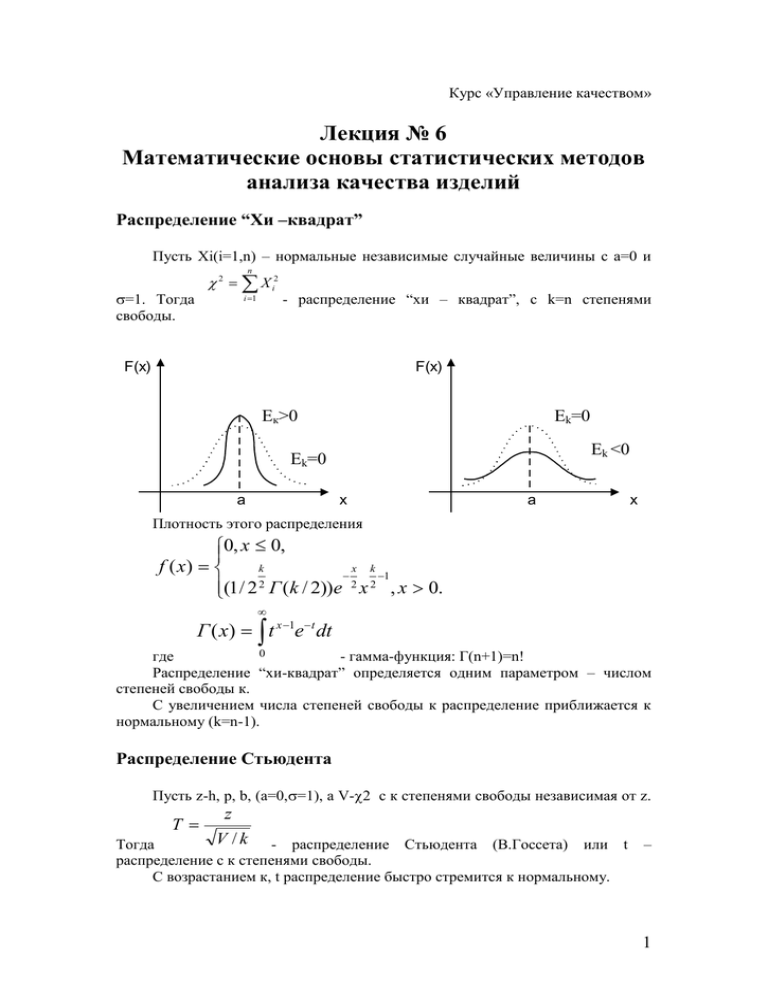
Курс «Управление качеством» Лекция № 6 Математические основы статистических методов анализа качества изделий Распределение “Хи –квадрат” Пусть Xi(i=1,n) – нормальные независимые случайные величины с а=0 и n 2 X i2 =1. Тогда свободы. i 1 - распределение “хи – квадрат”, с k=n степенями F(x) F(x) Ек>0 Ek=0 Ek <0 Ek=0 a x a x Плотность этого распределения 0, x 0, f ( x) k x k 1 2 2 2 ( 1 / 2 Г ( k / 2 )) e x , x 0. Г ( x) t x 1e t dt 0 где - гамма-функция: Г(n+1)=n! Распределение “хи-квадрат” определяется одним параметром – числом степеней свободы к. С увеличением числа степеней свободы к распределение приближается к нормальному (k=n-1). Распределение Стьюдента Пусть z-h, p, b, (a=0,=1), а V-2 с к степенями свободы независимая от z. T z V /k Тогда - распределение Стьюдента (В.Госсета) или t распределение с к степенями свободы. С возрастанием к, t распределение быстро стремится к нормальному. – 1 Распределение Фишера – Скидекора Пусть U и V независимые случайные величины, распределенные по закону F Х2 со степенями свободы соответственно к1 и к2. Тогда распределением Фишера-Снедекора. Плотность распределения U / k1 V / k 2 называют 0, x 0 f ( x) x ( k1 2) / 2 C0 (k k x)( k1 k 2 ) / 2 , x 0 2 1 , где к к2 к1 / 2 к 2 / 2 Г 1 к1 к2 2 C0 Г (к1 / 2) Г (к2 / 2) Распределение Вейбулла Данный закон получен для объектов, которым присущи усталостные явления. Например, вакуумные приборы электромеханические изделия, шарикоподшипники и др. Плотность распределения отказов описывают зависимостью, f (t ) T0 e 1e t / T0 , где - число отказов, на которые ведется расчет; Т0 – среднее время между отказами. Вероятность безотказной работы равна p(t ) et x / T0 . Кроме выборочных средней, дисперсии и среднеквадратического отклонения применяют и другие характеристики вариационнго ряда. Модой М называют варианту, которая имеет наибольшую частоту. Медианой ml называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Размахом варьирования R называют разность между наибольшей и наименьшей вариантами R=Xmax-Xmin. Средним абсолютным отклонением называют среднее арифметическое m m ni / x j xb / / ni i 1 i 1 абсолютных отклонений Коэффициент вариации V – это выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней 2 V=(/Xb)*100%. Предсказать значение случайной величины невозможно. Казалось бы, если существует множество случайных величин, то предсказать поведение большого числа случайных величин, тем более нельзя. Законы больших чисел Теорема Бернулли. Если в каждом из n независимых испытаний вероятность p появления события постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности p по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико, т.е. m вер m lim n P | p | 1, P n n Теорема Чебышева. Если х1,х2,…,хn попарно независимые случайные величины, а М(Хi) – их математические ожидания, а дисперсии их равномерно ограничены (D(Xi)<C), то как бы мало ни было >0, вероятность неравенства 1 n 1 n M ( xi ) xi n n i 1 i 1 случайных величин будет как угодно близка к 1, если число достаточно велико, т.е. 1 n 1 n lim P xi M ( xi ) 1. n n i 1 n i 1 На теореме Чебышева основан выборочный метод, используемый в математической статистике. Пусть х1, х2,…, хn – последовательность независимых случайных величин, каждая из которых имеет конечные М(Х) и D(Х). M ( X k ) ak , D( X k ) bk2 Введем обозначение n n i 1 k 1 n S n X k , An ak , B bk2 2 n k 1 Обозначим S An Fn ( x) P n x Bn К последовательности X1, X2,…, Xn применима центральная предельная теорема, если при любом х функция распределения нормированной суммы при n стремится к нормальной функции распределения, т.е. S An lim P n x n Bn 1 2 x Z e 2 /2 dz Если выполнены следующие условия: все Х1, Х2,…,Хn – одинаково распределены; 3 D(X1), D(X2),…,D(X3) – конечны и отличны от нуля; Для >0, n Cn lim Ln lim 2 0, Cn M X k ak n Bn k 1 2 (условие Ляпунова), то к последовательности Х1, Х2,…,Хn применима центральная предельная теорема. Сущность условия Ляпунова состоит в требовании, чтобы каждое слагаемое суммы (n-Аn)/Bn оказывало на сумму ничтожное влияние. 4











