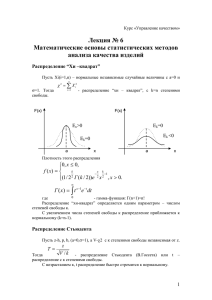
Интервальные оценки параметров распределения
реклама

{ интервальные оценки параметров - некоторые распределения СВ связанные с нормальным распределением доверительный интервал для выборочного среднего при известной дисперсии - доверительный интервал для
дисперсии при известном математическом ожидании - доверительный интервал для дисперсии при неизвестном
среднем - доверительный интервал для среднего при неизвестной дисперсии }
Статистика ã i , используемая в приближенном равенстве ã i = a i называется
точечной оценкой неизвестного параметра по выборке.
Пример:
~ 1
m
x
n
n
xi
i 1
~
Dx
n
n 1
1
n
n
2
~ 2
x
m
x
i
i 1
f(x)
x
~
mx m
x
Точечные оценки ã i не совпадают (за исключение редких случаев) с
истинным значением неизвестных параметров a i .
Всегда имеется некоторая погрешность при замене неизвестного параметра
его оценкой, т.е. | ã (x1, x2 , …, xn ) – a| < e :
a
e
ã
x
l
P (| a a | e ) P ( e a a e ) P ( a e a a e )
~
~
Если эта вероятность близка к единице P ( a e a a e ) g
то диапазон практически возможных значений ошибки, возникающей при замене ã
на a равен e .
Чем меньше будет e , тем точнее оценка ã .
Вероятность того, что интервал ( ã - e; ã + e ) со случайными границами
накроет неизвестный параметр a , равна 1 - 2e = g .
Эта вероятность называется доверительной вероятностью.
Доверительным интервалом уровня g для параметра ã выборки
X = ( x1, x2, …, xn ) из генеральной совокупности F ( x, a ) называется
интервал ( ã (1), ã (2)) со случайными границами, такой что:
Pa ( a~ ( 1 ) ( x ) a a~ ( 2 ) ( x )) g
Число g называется доверительным уровнем интервала. Оно характеризует
надежность этого интервала. Увеличивая длину интервала, мы увеличиваем
надежность. Но при этом уменьшается точность оценки.
L 2 e M ( a~ ( 2 ) a~ ( 1 ) )
Найти оптимальное решение по всем объектам как правило невозможно.
Один из способов: задаться надежностью (обычно это число близкое единице:
0.9; 0.95; 0.99) и затем попытаться найти из всех интервалов уровня g такой ,
у которого длина L будет наименьшей, то есть оценка будет наиболее точной.
Пусть x1 , x2 , …, xn есть независимые СВ, имеющие стандартное нормальное
распределение. Распределение суммы квадратов этих величин называется
распределением Хи-квадрат с n степенями свободы.
n2 x12 x22 ... xn2
f(x)
0.5 -
n=1
n
x
1
1
x2 e 2, x 0
n
f( x ) 22 ( n )
2
0
, x 0
( m)
n>2
n=2
Плотность распределения
Charles Pearson
(1857-1936)
t m 1
e
t dt
0
x
Мах в точке x = n - 2
Гамма функция Эйлера
F 2 ( s )
n
s
p
0
2
n
Плотность распределения Пирсона
( x ) dx
n
x
1
1
x2 e 2, x 0
n
f( x ) 22 ( n )
2
0
, x 0
p 2 ( x )
n
( m ) e tt m 1 dt
Гамма функция Эйлера
0
F 2 ( h( n ) )
h( n ) ( 0 1 )
n
x
h( s )
Пусть x1, x2 , …, xn , x0 есть независимые СВ, со
стандартным нормальным распределением.
Распределением Стьюдента с n степенями
свободы называют распределение
tn
x0
x12 x22 .... xn2
ft ( x )
( m)
n
0.4 -
Плотность распределения
n 1
n 1
2
(1 x ) 2
n
n
n
2
2
e
t m 1 dt
t
0
f(x)
n
Сходится к СНЗ
n=1
x
-1
1
William Gosset
(1876 – 1937)
Пусть даны случайные величиныx1 , x2 , …, xn , xn+1 , xn+2 , …, xn+m - независимые СВ, имеющие
стандартное нормальное распределение и величины, имеющие распределение хи-квадрат с
n и m степенями свободы соответственно. Распределением Фишера со степенями свободы
( n, m ) – называется распределение Fn , m
Fn ,m
Плотность распределения
m
n
2
n
2
m
n m
n
1
n m
2
x
2
f( x)
n2m 2
n m , x 0
n m
2
( m nx )
2 2
f(x)
1
Ronald Fisher
(1890 – 1962)
x
x = (n-2)m/n(m+2)
Предположим, что параметр m неизвестен, а дисперсия s 2 известна.
x1 x2 .. x n nm
FG (t) = F(t)
G ( x1 , x2 ,.., x n , m )
s n
t2
1
1
2
F ( ue ) e
ue
e dt e F ( ) F ( ue ) e
2
2 ue
D
eg
~
s
~
P (| m m | e ) 2 F (
) 1
m
n
s m~
eg
1 g
~ e ;m
~ e )
e
s
arg
F
(
)
2F (
) 1 g
~
Ig ( m
g
m
g
g
2
s m~
1 g
~ t s ;m
~ t s )
Используется таблица tg arg F (
) Ig ( m
~
~
g m
g m
2
~ s t m m
~ s t
m
g
g
n
n
n
G(x1 ,x2 ,..,x n ,s )
2
2
(x
m)
i
i 1
s2
n
(
i 1
xi m
s
)2
Функция G(xнорм.) имеет хи-квадрат распределение с n – степенями свободы, не
зависящее от неизвестного параметра s2
Обозначая h (n)e- квантили этого распределения и фиксируя e1 + e2 = 1 - g
приходим к неравенству, выполняемому с вероятностью g
n
hε(n)
1
2
(x
m)
i
i 1
s2
h1(n)
ε2
n
(x
i 1
i
h
m)
(n)
1 ε2
n
2
s2
(x
i 1
i
m) 2
hε(n)
1
Оба параметра неизвестны. m – мешающий параметр. Функция G (xнорм.) имеет
хи-квадрат распределение с (n-1) – степенями свободы, не зависящее от
неизвестного параметра s 2
G(x1 ,x2 ,...,x n ; m, s )
2
1
s2
n
(x
i 1
i
~) 2
m
Обозначая h(n-1)e- квантили этого распределения и фиксируя e1 + e2 = 1 - g
приходим к неравенству, выполняемому с вероятностью g
n
(xi m~) 2
i 1
h
(n 1 )
1 ε2
n
s2
(x
i 1
i
~) 2
m
hε(n1 1 )
(n 1 )s 2
(n 1 )s 2
2
s
(n 1 )
h1 ε2
hε(n1 1 )
Выбирается функция G имеющая распределение Стьюдента с (n-1) – степенями
свободы.
G(x1 ,x2 ,...,x n ; m, s )
2
~ m)
n (m
1
n 1
n
~) 2
(x
m
i
~ m)
n (m
s
i 1
Обозначая t (n)e- квантили этого распределения и фиксируя e1 + e2 = 1 - g
приходим к неравенству, выполняемому с вероятностью g
~ s t (n 1 ) m m
~ s t (n 1 )
m
n ( 1 g)/ 2
n ( 1 g)/ 2
@
Найти доверительный интервал для среднего значения генеральной
совокупности при больших объемах выборки (n > 30)
n 100
По выборочным данным находим выборочные cреднее арифметическое для m и
стандартное отклонение S
Это точечные оценки
~
m
x
1
( 35 2 37 3 39 30 41 40 43 20 45 5 ) 40 .76
100
~
100
1
s Dx
(
( 35 2 2 37 2 3 39 2 30 41 2 40 43 2 20 45 2 5 ) ( 40 .76 ) 2 ) 2
99
100
@
Задаемся доверительной вероятностью : g = 0,95 .
Находим значение tj , соответствующее заданной доверительной
вероятности t0,05 = 1,96 .
s
s
~
~
mx 1.96
m mx 1.96
n
n
40.368 m 41.152
@
Для контроля качества в 40 пробах стали GS50 определялось содержание
углерода x (%С) и прочность на разрыв z (Н/мм ). Данные оформлены
в виде таблицы чисел:
X: 0.3, 0.33, 0.37, 0.36, 0.31, 0.29, 0.34, 0.39, 0.37, 0.38, 0.35, 0.32, 0.39, 0.3, 0.32,
0.32, 0.38, 0.37, 0.38, 0.33, 0.37, 0.33, 0.34, 0.33, 0.3, 0.34, 0.36, 0.33, 0.34, 0.36,
0.29, 0.3, 0.33, 0.32, 0.32, 0.38, 0.37, 0.34, 0.35, 0.36
X = X ( x1 , x2 , …, x40 ) – выборка объемом n = 40
Z: 589, 614, 612, 572, 548, 537, 574, 570, 540, 575, 535, 593, 582, 538, 566, 562, 601,
587, 587, 614, 602, 544, 545, 562, 576, 596, 605, 575, 570, 550, 572, 555, 555, 518,
539, 557, 558, 587, 580, 560
Z = Z (z1 , z2 , …, z40 ) – выборка объемом n = 40
@
Найти доверительные интервалы для mx и mz , теоретических
значений содержания углерода и прочности на разрыв стали GS50.
Напомним, что объем каждой из выборок : n = 40 .
Зафиксируем доверительную вероятность, близкую к единице : g = 0.95 .
По таблице распределения Стьюдента определим приближенно:
)
t0(.39
975 2.02
~ sx t ( 39 ) 0 .3415 0 .289 2 .02 0 .3415 0 .0092
m
x
0 .975
6 .32
40
~ sz t ( 39 ) 570 .05 24 .14 2 .02 570 .05 7 .71
m
z
0 .975
6 .32
40
0 .332 mx 0 .351
562 .2 mz 577 .8