Тема 5. Сезонные и параметрические модели временных рядов МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ

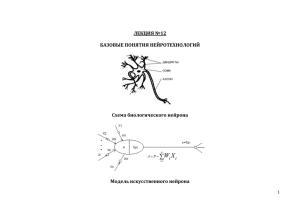
МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ
INTERNATIONAL BANKING INSTITUTE
Тема 5. Сезонные и параметрические модели
временных рядов
Целью изучения данной темы является создание базовой основы подготовки менеджеров по
специальности 080507 в области построения моделей различных задач в сфере экономики,
формирования у студентов систематизированного подхода к постановке и решению задач
прогнозирования. Предлагаемый курс позволит специалистам быстрее адаптироваться к
практической работе, лучше ориентироваться в научно-технической информации и литературе
по специальности, увереннее принимать решения, возникающие в работе.
Основными задачами изучения темы являются получение студентами углубленных
теоретических знаний по применению моделей прогноза, приобретение ими устойчивых
навыков выполнения научно-исследовательских работ, умения решать сложные научные
проблемы, связанные с построением моделей, включая и многомерные, способности к
логическому анализу полученных результатов и определению путей поиска приемлемых
решений.
Широко используемые методы математической статистики для решения задач прогноза в
ряде случаев не дают надежных оценок прогноза, что связано прежде всего с
неустановившимся характером временного ряда, наличием тренда, сезонных колебаний. В
такой ситуации целесообразно применить искусственные нейронные сети (ИНС), в основе
работы которых имеется определенная аналогия с работой мозга биологического объекта [6].
ИНС представляют собой системы, используемые при решении проблем, которые не могут
быть точно сформулированы. Слово «нейронные» применяется потому, что многое в теорию
ИНС пришло из нейробиологии, хотя моделирование функций мозга – совершенно другая
научная сфера, но из этой области в теорию ИНС заимствованы некоторые биологические
аналогии. На сегодняшний день традиционные методы организации вычислительного процесса
в ЭВМ оказываются неэффективными при решении ряда задач, относящихся к классам
неформализуемых или случайных, которые требуют обработки больших массивов информации,
проверки множества альтернативных гипотез, поиска в базах данных. Применение ИНС
позволяет привлечь в вычислительную технику метод обработки информации, характерный для
высокоорганизованных биологических систем, в частности, принцип параллелизма. В отличие
от фон-Неймановской архитектуры в традиционных ЭВМ в ИНС и компьютерах, построенных на
их основе, роль программирования выполняет обучение, под которым понимается изменение
состояния самих нейронов и связей между ними.
ИНС индуцированы биологией, так как состоят из элементов (искусственных нейронов),
функциональные возможности которых аналогичны большинству элементарных функций
биологического нейрона. Эти элементы затем организуются в структуру, называемую сетью,
которая может выполнять некоторые функции, свойственные в той или иной степени
биологическому мозгу. На вход искусственного нейрона поступает множество сигналов, каждый
из которых является выходом другого нейрона. Каждый вход умножается на соответствующий
вес, аналогичный синаптической силе биологического нейрона, и все произведения
суммируются, определяя уровень активации нейрона. На рис. 5.1 представлена модель,
реализующая эту идею.
Хотя сетевые парадигмы весьма разнообразны, в основе почти всех лежит эта конфигурация.
Множество входных сигналов x1, x2,... , xn поступает на искусственный нейрон. Каждый сигнал
умножается на соответствующий вес w1, w2,... , wn и поступает на суммирующий блок Σ,
который складывает алгебраически взвешенные входы, создавая выходной сигнал s. Далее
сигнал s преобразуется функцией активации F(s), которая вырабатывает выходной нейронный
сигнал Y=F(s).
Несмотря на то, что один нейрон и способен выполнять простейшие процедуры
распознавания, сила нейронных вычислений проистекает от соединений нейронов в сети.
1
МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ
INTERNATIONAL BANKING INSTITUTE
Рис. 5.1 Искусственный нейрон
Топология ИНС – это логическая (иногда физическая) структура, в которой множество узлов
(ячеек, нейронов) соединены друг с другом с помощью синапсов. Такая топология в некоторой
степени имитирует структуру биологических прототипов. В электронной реализации узлы сети в
общем случае являются операционными усилителями, а синапсы – переменными резисторами.
Вариант оптического осуществления ИНС определяет нейроны как источники света, а синапсы –
как оптическую среду с переменным коэффициентом преломления. В любом случае
долговременная память сети представляется состояниями синаптических связей между
нейронами, в то время как кратковременная память – состояниями самих нейронов. Оба вида
запоминаемой информации определяют характер отклика сети на входные воздействия.
Топология связей и правила, используемые любой сетью, обычно определяют парадигму
(модель или образ) сети. Некоторые ИНС применяют топологию с полностью соединенными
нейронами, другие имеют связи только между слоями сети, но не внутри. Выбранная топология
и правила работы сети устанавливаются исследователем для реализации выбранной парадигмы.
ИНС предназначены в первую очередь для решения двух проблем: классификации и
регрессии. Применительно к задаче прогноза временных рядов нас интересует проблема
регрессии, т. е. аппроксимации временного ряда и его экстраполяции на определенный
горизонт прогноза.
Однослойные нейронные сети не могут выполнять некоторые достаточно простые задачи, к
примеру, проблему исключающего ИЛИ. Переход к многослойным нейронным сетям, способным
решать более сложные задачи, был затруднен из-за отсутствия обучающего алгоритма для
таких сетей. Метод обучения многослойных сетей, получивший название метода обратного
распространения ошибки (ОРО), был открыт в 1986 г., после чего начался интенсивный период
разработки нейросетевых технологий на основе многослойных сетей в приложениях к
различным сферам науки и техники.
В задаче прогнозирования идея использования ИНС сводится к тому, чтобы по имеющемуся
временному ряду обучить сеть (настроить ее синаптические веса), а затем по обученной сети
оценить прогнозируемые значения. В такой постановке часто применяется метод погружения,
цель которого состоит в том, чтобы использовать во временном ряде два окна
W iи
W k зафиксированных размеров n и m, соответственно, для изучения заданного набора данных.
Для заданных размеров окон выдвигается предположение, что последовательность значений
W0i ,..., Wni ,
так или иначе связана со следующей последовательностью
W 0k ,...,W mk ,
и эти
отношения, хотя и неизвестны, но определены полностью в пределах набора данных.
Различные методы могут далее использоваться, чтобы найти корреляцию двух наборов
k
k
i
i
0 ,..., Wn и W 0 ,...,W m ). В случае нейронных сетей
значений ( W
W i W k
используется как
обучающийся вектор. Рис. 5.2 иллюстрирует общую схему метода, иногда называемого методом
скользящих окон.
2
МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ
INTERNATIONAL BANKING INSTITUTE
Рис. 5.2. Схема скользящих окон
При предсказании временного ряда окна сдвинуты во временном ряду с фиксированным
i
k
размером шага s (s<<n). Необходимо найти корреляцию вида: W 0...n  W 0...m , при
смещении окон во временном ряду с шагом s. Выбор размера окна и размера шага критично
влияют на способность любой системы предсказания идентифицировать регулярность, и таким
образом аппроксимировать скрытую связь точно. Кроме того, весьма часто требуется некоторая
предварительная обработка наборов данных, чтобы получить разумную отправную точку для n,
m и s.
Математически задача прогноза формулируется следующим образом. Пусть для временного
ряда X=(x1, x2,…, xn) требуется построить его продолжение X`=(x1, …,xn, xn+1, xn+2). Обычно
очередное значение временного ряда прогнозируется по некоторому числу его предыдущих
значений (прогноз на один шаг вперед во времени). После того, как вычислено очередное
предполагаемое значение, оно подставляется обратно и с его помощью (а также предыдущих
значений) получается следующий прогноз – это называется проекцией временного ряда.
Разобьем временной ряд на окна длиной l+1: x1, x2,…, xl, xl+1, x2, x3,:, xl+1, xl+2, … , xk, xk+1,:, xl+k1, xn и построим ИНС в виде двухслойного персептрона, имеющего l входов на нулевом
(входном) слое, слой скрытых нейронов с подбираемым числом нейронов и выходной слой с
одним нейроном.. Обучим его с помощью алгоритма обратного распространения на основе
следующей обучающей последовательности: xi, xi+1,…, xl+i-1  xl+i, i=1… n - l.
Для используемой сети в виде двухслойного персептрона наиболее приемлемым способом
обучения является метод ОРО. Сущность этого метода заключается в последовательном
прохождении сигналов «вперед» и «назад» по всем слоям сети. При проходе «вперед»
вычисляется значение выхода, которое сравнивается с его требуемой (целевой) величиной из
окна Wk. На основании разницы между этими двумя значениями вычисляется ошибка, которая
распространяется в направлении «назад» по сети, и методом градиентного спуска определяется
величина изменения весов в каждом слое. При измененных весах на вход предъявляется новый
входной вектор Wj, и процесс повторяется до тех пор, пока разница между выходным и
требуемым сигналами не станет достаточно малой. Таким образом, задача обучения в этом
методе сводится к предъявлению множества обучающих пар «вход - выход», за которые
принимаются значения уровней ряда из окон, изменению весов после каждого прохода по сети
«вперед» и «назад» до достижения приемлемой (заранее заданной) ошибки обучения.
Сеть должна иметь достаточное количество связей для запоминания последовательности.
Значение хn+1 снимается с выхода построенной выше нейронной сети при подаче на вход
следующего вектора (xn-l+1, xn-l+2,…, xn), (n – длина исходного временного ряда; l – размер
окна). Значение хn+2 находится аналогично при подаче на вход сети вектора (xn-l+2, xn-l+3,:,
xn+1). Таким образом, можно продолжать исходный ряд сколь угодно долго, находя следующие
значения на основе предыдущих.
В качестве иллюстративного примера использования предложенной методики построим
прогнозные
характеристики
временного
ряда,
отображающего
объем
пассажирских
авиаперевозок на протяжении 12 лет. Эти данные приведены в базе данных пакета Statistica
3
МЕЖДУНАРОДНЫЙ БАНКОВСКИЙ ИНСТИТУТ
INTERNATIONAL BANKING INSTITUTE
Neural Networks. На рис. 5.3 показан результат прогноза на 6 месяцев вперед, полученного с
помощью этого пакета.
Рис.5.3. Результат прогноза
Из рис. 5.3 видно, что прогнозируемый ряд достаточно хорошо аппроксимирует исходную
последовательность и, как следствие, дает достаточно надежную оценку прогноза на 6 месяцев
вперед.
Библиография
1. Басовский Л. Е. Прогнозирование и планирование в условиях рынка. – М.: Инфра - М,
2003.
2. Бокс Дж., Дженкинс Г. Анализ временных рядов. Вып. 1. Прогноз и управление. – М.:
Мир, 1974.
3. Боровиков В. П., Ивченко Г. И. Прогнозирование в системе Statistica в среде Windows. –
М.: Финансы и статистика, 1999.
4. Дюк В. Обработка данных на ПК в примерах. – СПб.: Питер, 1997.
5. Ивченко Б. П., Мартыщенко Л. А., Иванцов И. Б. Информационная микроэкономика.
Часть 1. Методы анализа и прогнозирования. – СПб.: Нордмед-Издат, 1997.
6. Кричевский М. Л. Введение в искусственные нейронные сети: Учеб. пособие. – СПб.:
СПб. Гос. Морской техн. ун-т, 1999.
7. Сошникова Л. А., Тамашевич В. Н., Уебе Г. и др. Многомерный статистический анализ в
экономике. – М.: Юнити-Дана, 1999.
4