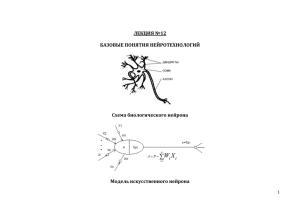
Проф. Райков А.Н. Лекция 9. Нейронные сети Идея

Проф. Райков А.Н.
Лекция 9. Нейронные сети
Идея коннекционистской модели обработки информации заключается в
том, что знания преимущественно хранятся в связях элементов. Эта модель
позволяет быстро обрабатывать значительные объемы информации за счет
нетрадиционного запараллеливания операций. Нетрадиционность заключается в том, что процесс не всегда алгоритмизируем, не всегда логически представим. На основе таких моделей стало возможным моделирование восприятия объектов в их естественном окружении, моделирование понимания текстов и планирования контекстуально релевантных действий.
Когда говорят о системах поддержки решений (СПР) имеют, прежде
всего, в виду системы, которые дают решение проблем на основе анализа уже
имеющихся в системе описаний аналогов (прототипов, случаев, кэйсов) похожих проблем. Чем таких кэйсов больше, тем охват проблемы считается
полнее, а эффективность работы системы, как правило, лучше. Назовем такую систему кейс-решателем. Парадигма кэйс-решателя достаточно эффективно работает в условиях плохо-структурируемых проблем. До недавнего
времени большинство кейс-решателей использовали символьно-логический
подход обработки данных (экспертные системы). Такой подход страдал низкими адаптивными свойствами, плохо учитывающим предпочтения различных пользователей. Системы были слишком статичны, невосприимчивы к
развитию. Для преодоления этого недостатка используется искусственные
нейронные сети (ИНС).
Нейронные сети строят модели на базе применения простой компьютерной эмуляции биологических нейронных систем. Они “пытаются” обучиться на примерах реального опыта, просеивая данные для поиска взаимосвязей, автоматически строя модели, “запоминая” примеры, корректируя
снова и снова ошибки. ИНС дают хорошие результаты и в условиях неполноты данных.
Перед любой проектной группой стоит задача прогнозной оценки времени окончательного завершения разработки проекта некоторого строительного продукта (изделия). Это не простая задача, поскольку на ответ сильно
влияют постоянно изменяющиеся факторы: вид сырья, конъюнктура, уровень
специалистов и др.
Эксперты, специалисты обычно понимают процесс и знают довольно
хорошо, как различные факторы воздействуют на качество вашего изделия.
При этом, уже имеется некоторые попытки, когда группа начинала разрабатывать подобные изделия. Через какое-то время накапливается достаточный
опыт для того, чтобы корректно решать задачи при ограниченном времени.
Накопленный опыт даже позволяет по аналогии оценивать новые задумки.
Почему появляется такая возможность? Ведь обучаются на относительно различных примерах. Пробуют поставлять изделия при различных
наборах условий. Не последнее место в этой оценке занимают комбинации
факторов (входных параметров, входов) и их взаимодействие. Понимание
этих взаимодействий - по существу это умственная модель для принятия хороших решений, выгодной оценки проектов. Это обобщение, модель. Ее
можно теперь использовать для экспертизы других исходных данных, даже
тех, с которыми группа никогда не имела прежде дело.
Конкретизируем пример. Пусть группа рассматривает размер (сложность) проекта строительного изделия и время, отведенное для его реализации. При этом, меру сложности грубо можно определять и измерять, например, в терминах “функциональных точек”, подлежащих исполнению по каждому примеру проекта (точки). За годы становления группа опробовала различные значения этих комбинаций, наблюдая в каждом случае качество решения. Качество, например, определялось по стоимости и времени. Однако,
хотя фиксировались все результаты в компьютере, вспомнить и охватить все
нюансы отдельных решений, естественно, не представлялась возможным - не
говоря уже об обобщениях.
Ведь запись отдельных данных только сообщает то, что связано со специфическим одиночным проектом. Возможно, посмотреть тренд какогонибудь параметра. Однако все это полезно, только если нужно повторить
точно такой же самый проект в точно таких же условиях. Но так не бывает. В
реальной практике одной или двух экспериментальных точек недостаточно,
чтобы понять, как запустить процесс в новых условиях. Что-то наверное
можно взять из смежного опыта? Но это не всегда лежит в рамках человеческих возможностей.
Когда точек достаточно, появляется возможность получать более
обобщенную картину. На рисунке можно показать в некоторой форме обобщенные результаты проектирования, скажем, сотен изделий различной сложности с различными предельными ограничениями. Например, при построении трехмерной столбиковой диаграммы высота столбца указывает качество
готового изделия в каждом случае (времени и стоимости). Итоговая картина
может быть сглажена путем интерполяции диаграммы - тогда получается непрерывная гиперповерхность.
Гиперповерхность представляют собой модель. Это - интерполяционное обобщение: большая часть поверхности не относится к каким-либо конкретным точкам. Поверхность может теперь использоваться, чтобы делать
прогнозные оценки, предсказывать качество изделия планируемой сложности. Причем, предсказание возможно даже если не анализировать детали
опытных данных по конкретным точкам. Чем сложнее изделие, тем сложнее
поверхность. Иногда трехмерного представления уже явно не хватает. Тем не
менее эксперты умственно справляются и с более сложными ситуациями.
ИНС также способна обучаться и строить модели на основе анализа
данных. С их помощью можно делать универсальный аппроксиматор - решатель для смежных проблем. Заметим, что в примере данные были разнотипные, а их элементы - взаимосвязанными. Для построения аппроксиматора,
конечно, нужно достаточно большое количество обучающих точек.
Первые теоретические результаты по ИНС появились в 1940-х годах
благодаря двум чикагским ученым (McColloh, Pitts). Большая работа была
2
сделана к середине 1950-х (McCarthy, 1956; Rosenblatt, 1957), когда исследователи создали простую ИНС в попытке промоделировать познавательные
(когнитивные) процессы обучения, происходящие в мозгу человека. Тогда
был построен перцептрон. Эти работы породили как всегда - оптимистов и
пессимистов. И только за последний десяток лет произошла окончательная
оценка значения ИНС - их польза была доказана на практике. ИНС хороши
для моделирования плохо понятных проблем, когда можно достаточно собрать опытных данных. При этом могут быть достигнуты более хорошие результаты по сравнению с использованием традиционных статистических,
численных методов.
Нейронная сеть обучается распознавать ситуации через пробы и ошибки. Ей предъявляют опытный образец и, если она дает адекватный отклик, то
с ней ничего не делают. Если отклик неадекватен, то ее, соотвественно, перестраивают. Этот процесс “прогоняют” сотни и тысячи раз на одной и той же
обучающей выборке, пока не будет достигнуто удовлетворительное качество
распознавание образцов.
Источники принципов, выделяющих ИНС из других технологий, лежат
в биологии. В биологических условиях наши умственные способности, скорее всего, существуют благодаря наличию сети индивидуальных но взаимосвязанных ячеек нервов - нейронов. Число нейронов в головном мозге человека достигает 1010, а может быть и больше. Нейроны - функциональные
единицы нервной системы. Они восприимчивы к раздражению, способны
возбуждаться и передавать электрические импульсы. Это дает возможность
связывать рецепторы (органы, воспринимающие раздражение) и эффекторы (органы, отвечающие на раздражение). В каждом нейроне можно различать тело клетки диаметром 3-100 мкм, которое содержит ядро, и различное
число отходящих от клетки отростков. Отростки, проводящие импульсы к
телу клетки, называют дендритами. Они короткие и распадаются на тонкие
терминальные ветви. Отростки, проводящие импульс от тела клетки, называются аксонами. Их длина может достигать нескольких метров. Аксон распадается на многочисленные тонкие веточки со вздутиями на концах. Он соединяется с соседними нейронами в участках, называемых синапсами. Синапсы бывают возбудительными и тормозными.
Нейрон может получать информацию из внешнего мира через различные точки нейронной сети. Например, когда Вы входите в ярко освещенную
комнату, нейроны ваших глаз регистрируют уровень яркости в определенных
участках памяти. Раздражающая информация называется стимулом. Стимулы
обрабатываются вашим мозгом и возбужденной системой. Информация “путешествует” по нейронной сети, генерируя новые внутренние сигналы от
нейрона к нейрону. Эти новые сигналы в конечном счете производят ответ,
отклик.
Нейрон передает информацию соседнему нейрону биохимическим способом. Этот процесс называется нейротрансмиссией. Наиболее простой и наглядный способ представления этого механизма - система электронноимпульсной передачи информации от одного нейрона к другому (“излуче3
ние” нейрона). Важно понять биологический факт, который полезен для понимания, как ИНС работают. Оказывается, когда информация нейроном получена, она либо возбуждает его, либо закрывает (накладывает запрет). Если
нейрон возбуждается достаточно сильно (выше некоторого порога), то он излучает по синапсу сигнал другому нейрону. С другой стороны, если получающий нейрон накладывает запрет, он не будет “излучать”. Тогда информация демпфируется, глохнет. Главное, что делает нейрон - это обработка информации, поступающей на ряд его входов и излучение ее дальше при условии, что она важна (по некоторому критерию).
Синаптические соединения могут быть подтверждены, усилены (обучение) или ослаблены (забыты) через некоторое время и в различных ситуациях. Через процесс обучения Вы можете устанавливать новые ответы на совершенно новые стимулы, изменять старые. Например, водитель без размышлений резко тормозит машину, если загорается стоп-сигнал впереди
идущего автомобиля. Еще пример: обучение ребенка броскам мяча в баскетбольную корзину.
Как эта биологическая аналогия реализуется в компьютере? Подобно
биологическому дубликату, искусственная нейросеть включает систему нейроузлов (узлы) и весов их соединений (эквивалент синапсов) в памяти компьютера. Узлы - это места расположения (хранения) данных, подобно переменным в программах, ячейки в электронной таблице. Узел аналогичен биологическому нейрону, но намного более простой. В ИНС узлы обычно размещаются по уровням, между уровнями устанавливаются соединения. На рис. 9.1
показано то, что могла бы собой представлять концептуально простая нейронная сеть. Круги представляют узлы, а линии - связи.
В принципе, ИНС функционирует таким же образом, как биологический прототип. Данные поданы в сеть, данные - обработаны с учетом связей,
результат подан на выход. На рис. 9.1 видно, что ИНС делится по уровням:
входной уровень, уровень обработки, уровень отклика - выходной уровень.
Чтобы понять, как ИНС обучают давать точные догадки, необходимо
понять влияние весов связей нейроузлов на формирование выхода нейрона.
Обучение в ИНС - это настройка весов. Но перед тем, как мы покажем способ настройки весов, сначала поймем, что происходит с входными данными
на уже обученной сети.
Для этого надо подробней посмотреть на работу искусственного нейрона (рис. 9.2, 9.3, 9.4). Нейрон может делать несколько простых вещей. Он
может собирать гроздь входных данных (сигналов), критически оценивать
собранное и обрабатывать информацию. Затем нейроузел пропускает обработанную информацию на следующий уровень. Если следующего уровня
нет, то этот сигнал будет откликом сети.
4
Выходной
уровень
Вывод,
догадки
Внутренняя
обработка
Скрытый
уровень
Входной
уровень
Данные
Рис.
15.9.1.
Простая
нейронная
сеть
Рис.
Простая
нейронная
сеть
На рис. 9.1 каждая линия - это вход из нижележащего уровня. Тело
нейрона состоит из двух секций. Нижняя секция комбинирует все входные
сигналы и суммирует их величины. Верхняя секция по этой сумме рассчитывает уровень важности входа. По результату этой обработки формируется
выход.
Для того чтобы проследить, как срабатывает нейроузел, обратимся к
рис. 9.2, 9.3. Сумма входов преобразуется в выходную величину с помощью
функции, называемой функцией преобразования. В качестве примера этой
функции выбрана монотонно непрерывная функция, определенная на области всех возможных значений суммы входов и областью определения от 0 до
1. При большом отрицательном значении суммы входов ее значение близко к
нулю, при большом положительном значении - единице, при нулевом значении - 0,5. Каково назначение этой функции?
Функция преобразования служит созданию “тупого” переключателя,
делающего нейрон включенным или выключенным - что зависит от характера входа. Функция определяет, с какого момента нейрон будет излучать. Поскольку функция носит S-образную форму (сигмоидальная), она добавляет
нелинейность в работу сети. В результате - степень изменения выхода зависит от точки открытия нейроузла.
Таким образом, основу каждой ИНС составляют относительно простые,
в большинстве случаев – однотипные, элементы (ячейки), имитирующие работу нейронов мозга. Каждый нейрон характеризуется своим текущим состоянием по аналогии с нервными клетками головного мозга, которые могут
быть возбуждены или заторможены. Он обладает группой синапсов – однонаправленных входных связей, соединенных с выходами других нейронов, а
также имеет аксон – выходную связь данного нейрона, с которой сигнал
(возбуждения или торможения) поступает на синапсы следующих нейронов.
5
Выход
Каждый синапс характеризуется величиной синаптической связи или ее весом wi, который по физическому смыслу эквивалентен электрической проводимости.
-
+
Сумма
Суммирование
входов
+
+
+
Рис. 9.2. Внутренность
искусственного
Рис. 16. Внутренность
нейрона нейрона
Текущее состояние нейрона определяется, как взвешенная сумма его
входов:
n
s = ∑ x i ⋅ wi .
i =1
Выход нейрона есть функция его состояния:
y = f(s).
Рис. 9.3 а) функция единичного скачка; б) линейный порог (гистерезис); в)
сигмоид – гиперболический тангенс; г) сигмоид формула (3)
Нелинейная функция f называется активационной и может иметь различный вид, как показано на рисунке 9.3. Одной из наиболее распространенных является нелинейная функция с насыщением, так называемая логистическая функция или, как уже сказано выше, сигмоид (т.е. функция S-образного
вида):
f ( x) =
6
1
1 + e − αx
При уменьшении α сигмоид становится более пологим, в пределе при
α=0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении α
сигмоид приближается по внешнему виду к функции единичного скачка с
порогом T в точке x=0. Из выражения для сигмоида очевидно, что выходное
значение нейрона лежит в диапазоне [0,1]. Одно из ценных свойств сигмоидальной функции – простое выражение для ее производной:
f ' ( x ) = α ⋅ f ( x ) ⋅ (1 − f ( x ))
Следует отметить, что сигмоидальная функция дифференцируема на
всей оси абсцисс, что используется в некоторых алгоритмах обучения. Кроме
того, она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон.
ДА
-
НЕТ
+
Большой положительный вход
дает сильный выход
-
???
+
Большая отрицательная сумма дает почти
нулевой выход
+
Сумма в районе
нуля порождает
только вопросы
Рис 17. Иллюстрация
функции функций
преобразования
Рис. 9.4. Иллюстрация
интерпретации
преобразования
Из сигмоидальных функций за счет комбинирования промежуточных
уровней могут быть построены более сложные функции. При этом форма
графика зависит от значения весов передаточных связей и числа промежуточных узлов. Могут быть получены кривые самой затейливой формы (рис.
9.5).
Теперь встает вопрос об обучении сети на основе имеющихся опытных
данных. Он не тривиален. Для иллюстрации возьмем типичную ситуацию
предсказания некоторой экспортно-импортной фирмой обменных курсов валют на базе данных истории (рис. 9.6). Пример показывает, что в течение четырех предыдущих дней курс валюты рос (кодируется 1), вырос он и в текущий день. Тогда, согласно опыта - завтра будет падение курса (кодируется 0).
Для этого примера можно построить и обучить очень простую ИНС. В ней на
вход подается четыре единицы, а на выходе получается ноль (рис. 9.7). С помощью этой же конфигурации можно получить и положительный выход. Для
7
этого веса надо сделать положительными). О правильном отклике сети иногда говорят, как о “догадке”. Более интересен случай с двумя образами (рис.
9.7, 9.8):
0011→0
(код первого образа)
1100→1
(код второго образа).
+1
-1
0,25
Выходной уровень
1
1
-0,5
1
1
3
-0,5
Входной уровень
Рис.Рис.
18. Внутренние
уровни форма
в сочетании
с весами
9.5. Возможная
графика
позволяют представлять сложные функции
4 дня назад 3 дня назад 2 дня назад вчера
1
1
1
1
сегодня
завтра
1
0
Входной код из 1 и 0
Рис. 9.6. Кодирование обменного курса
Рис. 19. Кодирование обменного курса валюты
Для адекватной обработки этого случая обученная сеть представлена
на рис 9.7. Заметим, что, если мы установим все веса очень маленькими положительными или очень маленькими отрицательными, результат будет
близким к нулю независимо от значений входного сигнала. Если значение
суммы входа близко к 0, выход равен около 0,5 и расположен точно между 0
и 1, - такой выход дает мало информации. В житейском смысле - это пожатие
8
плечами. Малые веса - говорят о малой чувствительности сети, плохой “догадливости” сети.
Итак, чтобы получить веса, обеспечивающие правильный вывод, надо
сеть обучить на основе обучающих примеров. Например, сначала все веса
делаются произвольно малыми. Затем сети предъявляют одну обучающую
запись, которую сеть обрабатывает для установки начальных весов.
Так как сеть еще не обучена, то, скорее всего, догадка при предъявлении очередной обучающей записи будет плохая. И это нормально, поскольку
неправильная догадка также содержит информацию, которая может использоваться для обучения. Важно не забыть, что любая информация нужна для
обучения и может быть использована для улучшения догадки в следующий
раз. Сеть на ошибках учится. Первое, что сеть делает при самообучении - это
сравнение результата вычислений с правильным (контрольным) выводом.
Отрицательные веса
0
a)
-
-
- -
1
1
1
1
+
-1-1-1-1=-4
Положительные веса
1
+
+
+ +
a)
+
1
1
1
1
20. Пример
обучения
сети
Рис. 9.7.Рис.
Пример
обучения
сети
+1+1+1+1=4
Если догадка соответствует правильному выводу, сеть ничего не делает
с собой. Если же догадка не соответствует контрольному результату, сеть
должна выяснить, в чем причина ошибки. Эта причина лежит в неправильном распределении весов связей нейроузлов. Они корректируются так, чтобы
распознавание приводило, в среднем, к правильным результатам.
9
1
a)
-
-
0
-
+ +
0
1
1
+
0+0+1+1=2
0
a)
-
-
+ +
-
1
1
0
+
0
-1-1+0+0=-2
Рис. 9.8.
обучения
образам
Рис.Пример
21. Пример
обучениясети
сети двум
двум образам
Другими словами, обучение сети должно приводить к минимизации
ошибки на обучающей выборке. Делать это надо по шагам.
Шаг 1: Делается вывод о догадке на основе имеющегося состояния весов и введенных входных данных.
Шаг 2: Вычисляется ошибка вывода. Например, если желательный вывод был 1, а сеть дала 0, ошибка составит +1 (вычисляется как разность 1 и
0).
Шаг 3: Определяется, как сильно и в каком направлении каждое из
значений весов связей, инцидентных этому узлу, должно корректироваться.
Сделать это можно вычислив, какой вклад в ошибку дает каждая весовая
связь. Так, например, если значение вывода было слишком маленьким, сеть,
скорее всего, нуждается в увеличении маленьких положительных или
уменьшении отрицательных весов связей. В сущности, здесь используется
информация (обратная связь) для оценки возможных вариантов разрешения
ошибки.
Шаг 4: Корректируются веса каждого узла. Например, в узле, где вывод был слишком маленький, пробуют увеличить значения положительных
весов. Это подогнало бы значение выхода ближе к желаемой 1. Можно также
попробовать уменьшать размер отрицательных весов или даже сделать их
положительными.
Шаг 5: Повторить процесс, выполняя подобный набор вычислений
(шаги 1 - 3) для каждого узла скрытого уровня. При этом анализируется чувствительность узлов для того, чтобы определить насколько велика ошибка,
привносимая каждым из узлов. Эта проверка ошибок и настройка весов продолжается для каждого скрытого уровня сети. Процесс называется “догадка обратная связь - настройка”.
10
Проблемы оптимизации состоят в поиске наиболее высоких пиков на
ландшафте (гиперплоскости) плохих решений. Работа оптимизационных методов состоит в поиске высоких пиков там, где сосредоточены хорошие решения. Картину ошибок нейросети можно представить в виде ландшафта,
размерность которого была бы представлена весами нейросети. Пики и впадины соответствуют ошибкам, причем пики - большим ошибкам, впадины меньшим. Но оптимизационная проблема нейронной сети состоит в том, чтобы настроить веса таким образом, чтобы минимизировать количество ошибок-догадок на обучающей выборке.
Способ, которым нейросеть находит нужные веса, называется методом
обучения. Он может быть контролируемым и неконтролируемым. В частности, рассмотренный выше метод обучения называется методом обратного
проникновения (back propagation). В этом методе ошибка между желаемым
выходом и фактическим “проникает” по сети обратно с одновременной настройкой весов.
Способы технической реализации нейросети разнообразны. Имеются,
конечно, аппаратные подходы к реализации нейросетей. Увлекательно перспективное направление реализации нейросетей на голографических элементах.
Применение нейросетей многообразно: в финансах1, в экономике, для
распознавания образов, в управлении транспортом и пр.2,3
Вопросы.
− Зачем статистическую обработку заменяют нейронной сетью?
− Решение на основе примеров - в чем фокус и проблема?
− Что делает искусственный нейрон?
− Что имеет своим прототипом настройка весов нейросети?
− Можно ли нейросеть обучить без примеров?
− Почему нейроузел не представить просто сумматором?
− Что такое сигмоидальная функция?
− Пример работы экспертной сети (например, в финансах)?
1
Бестенс Д.-Э., ван ден Берг В.-М, Вуд Д. Нейронные сети и финансовые рынки: принятие
решений в торговых операциях. М.: ТВП, 1997. – 236 с
2
Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. – М.:
Горячая линия – Телеком. 2001. – 382 с.
3
Романов В.П. Интеллектуальные информационные системы в экономике: Учебное пособие/од ред. д.э.н. Н.П.Тихомирова - -М.: «Экзамен», 2003. – 496 с
11