ОСНОВЫ СТАТ ТЕОРИИ РТС

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ
«НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ им. Р.Е. АЛЕКСЕЕВА»
В.А. Сьянов
ОСНОВЫ СТАТИСТИЧЕСКОЙ ТЕОРИИ
РАДИОТЕХНИЧЕСКИХ СИСТЕМ
Рекомендовано Учёным советом Нижегородского государственного
Технического университета им. Р.Е. Алексеева в качестве
учебного пособия для студентов высших учебных заведений, обучающихся
по направлениям «Радиотехника», «Радиоэлектронные системы и комплексы»
Нижний Новгород 2023
1
УДК 621.391
ББК
Рецензент
доктор физико-математических наук, профессор кафедры бионики и
статистической радиофизики Нижегородского государственного
университета им. Н.И. Лобачевского А.Г. Флаксман
Сьянов В.А.
Основы статистической теории радиотехнических систем: учеб.
пособие / В.А.Сьянов; Нижегород. гос. техн. ун-т им. Р.Е. Алексеева. –
Нижний Новгород, 2023. – с.
ISBN
Рассмотрены базовые положения теории вероятности, математической
статистики и теории случайных процессов. Уделено внимание методам описания и
преобразования стационарных случайных процессов в линейных радиотехнических
системах. Рассмотрены методы нелинейного безынерционного преобразования
стационарных случайных процессов.
Приведены методы синтеза и анализа оптимальных алгоритмов обработки
сигналов на фоне помех в системах связи и радиолокации. Рассмотрены
оптимальные алгоритмы обнаружения и различения детерминированных и
случайных сигналов на фоне аддитивного гауссовского шума. Уделено внимание
методам синтеза и анализа работы согласованных фильтров детерминированных и
случайных сигналов.
Рассмотрены статистические методы разрешения и оценки параметров
сигналов в условиях действия аддитивых гауссовских помех. Приведены функции
рассогласования простых и сложных сигналов. Рассмотрены методы оптимальной
оценки параметров сигналов на фоне гауссовского шума.
Предназначается для бакалавров, специалистов, магистров и аспирантов,
обучающихся по направлениям «Радиотехника», «Радиоэлектронные системы и
комплексы».
Рис. . Табл. .Библиогр.:
назв.
УДК 621.391
ББК
ISNB
©Нижегородский государственный
технический университет
им. Р.Е.Алексеева, 2023
© Сьянов В.А., 2023
2
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ……………………………………………………………
1. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ СОБЫТИЙ И ПРОЦЕССОВ
1.1. Элементы теории
вероятности…………….................................
1.1.1. Понятия и определения………..………………………
1.1.2. Сумма и произведение событий…………
1.1.3. Теорема вероятности зависимых событий………
1.1.4. Теорема
обратной
вероятности
зависимых
событий….
1.1.5. Теорема о повторении опытов…………… …………
1.2. Законы распределения………………………………………\
1.2.1. Законы распределения СВ……………………………
1.2.2. Числовые характеристики СВ………………………
1.2.3. Биномиальное распределение………………………
1.2.4. Нормальное распределение…………………………
1.2.5. Распределение Релея………………………………
1.2.6. Равномерное распределение…………………………
1.3. Статистическое оценивание параметров…………………
1.3.1. Выборочное среднее…………………………………
1.3.2. Выборочная дисперсия………………………………
1.4. Совокупность СВ………………………………………………
1.4.1. Функция распределения совокупности СВ………
1.4.2. Условные плотности вероятности многомерного СП.
1.4.3. Числовые характеристики совокупности СВ……
1.4.4. Стационарные СП…………………………………
1.4.5. Эргодические СП………………………………………
1.4.6. Спектральные характеристики СП…………………
1.4.7. Плотность вероятности гауссовского СП……………
1.5. Воздействие СП на линейные системы………………………
1.6. Нелинейное безынерционное преобразование СП……
1.6.1. Функциональное преобразование совокупности СВ
1.6.2. Функциональное преобразование двух СВ………
1.6.3. Преобразование декартовых координат в полярные
1.7. Примеры……………………………………………………
1.7.1. Теория вероятности………………………….
1.7.2. Случайные величины. Законы распределения………
1.7.3. Случайные процессы
1.7.4 СП в линейных системах
3
6
7
7
7
8
9
9
9
9
9
12
15
15
17
19
21
22
24
27
27
29
29
32
33
34
35
38
40
40
42
43
45
45
50
55
56
2.
3.
1.7.5. СП в нелинейных системах
ОСНОВЫ СТАТИСТИЧЕСКОЙ ТЕОРИИ ОБНАРУЖЕНИЯ
СИГНАЛОВ
2.1. Задачи статистической теории обнаружения сигналов
2.2. Обнаружитель сигналов
2.3. Обнаружение детерминированного сигнала
2.4. Характеристики обнаружения
2.5
Обнаружение сигнала со случайной начальной фазой
2.6. Характеристики обнаружения
2.7. Обнаружения сигнала со случайной амплитудой и
начальной фазой
2.8. Характеристики обнаружения
2.9. Согласованный фильтр
2.10. Частотная характеристика СФ
2.11. Свойства СФ
2.12. Обнаружение пачек импульсных сигналов
2.13. Когерентный обнаружитель пачки импульсов
2.14. Некогерентный обнаружитель пачки импульсов
2.15. Накопитель пачки импульсов с логикой «k из N»
2.16. Обнаружитель сигналов на фоне небелого шума
2.17. Различение двоичных детерминированных сигналов
2.18. Характеристики оптимального различителя сигналов
2.19. Примеры
2.19.1. Обнаружение детерминированных сигналов
2.19.2. Воздействие сигнала и шума на СФ
2.19.3. Различение сигналов
РАЗРЕШЕНИЕ СИГНАЛОВ
3.1. Понятие о разрешающей способности сигналов
3.2. Функция рассогласования сигнала
3.3. Функции рассогласования импульсных сигналов
3.4. Основы теории измерения параметров сигналов
3.5. Оптимальный алгоритм измерения параметров сигналов
3.6. Измерение параметров радиолокационных синалов
3.6.1.
Неследящие измерители дальности
3.6.2.
Неследящие измерители скорости
3.7. Следящие измерители параметров цели
3.8. Точность измерения радиолокационных параметров
3.8.1
Точность измерения временного запаздывания
3.8.2.
Точность измерения частоты
4
59
66
66
69
74
78
80
83
84
86
88
91
92
94
94
96
98
99
103
107
112
112
115
119
120
120
120
122
127
128
130
131
133
133
135
136
137
3.8.3.
Точность измерения угловой координаты
3.8.4.
Точность совместного измерения параметров
3.9. Примеры
3.9.1.
Функция рассогласования сигнала
3.9.2.
Точность определения джальности и скорости
ПРИЛОЖЕНИЕ
Нормированная функция Лапласа
СПИСОК ЛИТЕРАТУРЫ
5
138
139
141
141
144
146
146
148
ВВЕДЕНИЕ
Учебное пособие предназначено для бакалавров, специалистов,
магистров и аспирантов, обучающихся по направлениям «Радиотехника»,
«Радиоэлектронные системы и комплексы». Оно может быть использовано для
изучения теоретических основ методов синтеза и анализа оптимальных
алгоритмов обработки сигналов на фоне помех в рамках дисциплин
«Статистическая теория радиотехнических систем» и «Статистическая
радиотехника».
Необходимо отметить, что по данной тематике издано большое
количество учебников, учебных пособий и монографий [1-10]. Все они имеют
значительный объем, сложный математический аппарат, что затрудняет их
широкое использование в практической работе для студентов. Авторы
постарались в доступной форме изложить тот минимальный объем
информации,
который
позволяет
усвоить
теоретические
основы
статистических методов в системах радиолокации и связи для дальнейшего их
изучения.
В первой главе рассмотрены основы теории вероятности,
математической статистики, теории случайных процессов и их линейного и
безынерционного нелинейного преобразования. Для усвоения приведенного
материала даны задачи и примеры их решения.
Во второй главе пособия приведены методы и оптимальные алгоритмы
обнаружения и разрешения сигналов на фоне помех. Рассмотрены методы
синтеза и анализа согласованных фильтров простых и сложных сигналов. В
конце главы приведены задачи и рассмотрены методы их решения.
В третьем главе излагаются статистические методы разрешения и оценки
параметров сигналов в условиях воздействия аддитивых гауссовских помех.
Приведены функции рассогласования простых и сложных сигналов.
Рассмотрены методы оптимальной оценки параметров сигналов на фоне
гауссовского шума. В конце главы приведены задачи с решениями по тематике
теоретического материала.
Авторы надеются, что данное учебное пособие поможет облегчить
освоение теоретических основ статистической теории радиотехнических
систем студентам и аспирантам радиотехнических специальностей.
6
1. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ
СОБЫТИЙ И ПРОЦЕССОВ
1.1. Элементы теории вероятности
1.1.1. Основные понятия и определения
Теория
вероятностей
–
математическая
наука,
изучающая
закономерности массовых случайных событий и явлений.
Основные понятия:
Случайное событие – явление, которое может наступить или нет в N
опытах.
Пусть происходит N - кратное повторение опыта, в результате которого
случайное событие А происходит n раз.
В этом случае можно ввести относительную частоту события А
 ( A) 
n
.
N
При повторении серий опытов будем получать разные значения  ( A) .
При увеличении числа N частота события стремится к вероятности события А:
lim ( A)  p( A) .
N 
Основные свойства вероятности:
1. 0  P( A)  1;
2. P( A)  0;
3. невозможно е событие P( A)  0;
4. достоверно е событие P( A)  1;
5. противоположное событие P( A )  1  P( A).
Пусть в результате N испытаний возможно возникновение нескольких
событий A, B, C ,...
Справедливы следующие аксиомы:
1.
События A, B, C ,... равновероятны, если при одних и тех же
условиях они появляются с равными вероятностями.
2.
События A, B, C ,... несовместимые если в результате испытаний
невозможно возникновение двух и более событий одновременно.
3.
События A, B, C ,... составляют полную группу событий, если в
результате испытаний возникает хотя бы одно из них.
Классическое определение вероятности события А (по Лапласу) вводится
как отношение числа благоприятных исходов возникновения события к
общему числу испытаний P( A)  n N . При этом в соответствии с законом
7
больших чисел при N   имеем совпадение статистической вероятности
появления события P( A) с частотой его появления  .
При бесконечном числе исходов события А удобно ввести понятие меры
события. Например, при бросании точки в область G , с выделенной в ней
подобластью Q , в качестве меры вероятности удобно ввести площадь.
Вероятность такого события можно определить как отношение P( A) 
SQ
SG
. При
бросании точки в отрезок длины L и определения вероятности её попадания в
меньший длины отрезок l в качестве меры вероятности такого события удобно
ввести длину P( A) 
l
. Обобщая, можно ввести в качестве меры площадь,
L
длину, объем, вес и т.д. Представление вероятностей событий в виде областей
дает наглядную интерпретацию зависимых (независимых), совместимых
(несовместимых) событий, а так же их алгебраические преобразования.
1.1.2. Сумма и произведение событий
Пусть есть события А и В, получающиеся в результате N опытов.
Суммой называется событие C  A  B , состоящее в появление в
результате опыта хотя бы одного из этих событий.
C  A B ,
Произведением
называется
событие
состоящее
в
одновременном возникновении как события А так и В.
Теорема сложения вероятностей:
Для несовместимых событий P( A  B)  P( A)  P( B) ;
Для совместимых событий P( A  B)  P( A)  P( B)  P( A  B) .
Условная вероятность для зависимых событий.
Событие А называется статистически зависимым от событий B1, B2 ,..., Bn ,
если вероятность его возникновения зависит от того осуществилось событие
Bi или нет. В противном случае вероятность события А статистически не
зависит от возникновения событий B1 , B2 ,..., Bn . Для зависимых событий
вводится условная вероятность P( A / B1 , B2 ,..., Bn )
Теорема умножения вероятностей двух зависимых событий:
P( A  B)  P( A) P( B / A)  P( B) P( A / B) .
Теорема умножения вероятностей для n зависимых событий:
P( A1 , A2 ,..., An )  P( A1 ) P( A2 / A1 ) P( A3 / A1 A2 )    P( An / A1 A2    An 1 ) .
Следствия теоремы умножения:
1. Для статистически независимых событий А и В
P( A  B)  P( A) P( B / A)  P( B) P( A) .
8
2. Для статистически независимых событий A1 , A2 ,..., An
P( A1 , A2 ,..., An )  P( A1 ) P( A2 )    P( An ) .
1.1.3. Теорема полной вероятности зависимых событий
Пусть событие A может наступить только при условии появления одного
из событий H1, H 2 ,..., H n , составляющих полную группу несовместимых
событий. Пусть известны вероятности появления событий P( H i ) и условные
вероятности событий P( A / H i ) . Тогда полная вероятность события А равна
n
P( A)   P( H i ) P( A / H i ) .
i 1
1.1.4. Теорема обратной вероятности для зависимых событий
Пусть события H1 , H 2 ,..., H n составляют полную группу несовместимых
событий и событие А является случайным следствием возникновения события
H i . Пусть известны априорные вероятности появления событий P( H i ) и
условные вероятности событий P( A / H i ) .
Тогда условная вероятность события H i равна:
P( H i ) P( A / H i )
.
P( H i / A)  n
 P( H i ) P( A / H i )
i 1
1.1.5. Теорема о повторении опытов
Пусть производится N независимых испытаний при заданной
вероятности появления события А равной P( A)  p . Событие А состоит в том,
что в серии из N опытов оно происходит n раз.
Тогда вероятность события А будет равна:
PN (n)  CNn p n (1  p) N  n ,
N!
где CNn 
- биномиальный коэффициент.
n!( N  n )!
1.2. Законы распределения
1.2.1. Законы распределения случайных величин
Случайному событию А можно поставить в соответствие количественную
характеристику – случайную величину.
9
Случайной, называется величина , принимающая то или иное значение в
результате опыта (испытания).
Простейшая модель случайной величины – последовательность
независимых опытов (испытаний), когда в результате каждого очередного
испытания произойдет, либо не произойдет некоторое событие.
Случайные величины (события) можно разделить на два класса –
непрерывные и дискретные.
Дискретные – бросание игральной кости.
Непрерывные – бросание точки в интервал непрерывных числовых
значений.
Будем обозначать случайную величину (СВ)  , а случайные значения ей
принимаемые – x .
( x1 , x2 ,..., xn ) можно
определить,
известными
Дискретную
СВ
априорными
вероятностями
появления
соответствующих
значений
p( x1 ), p( x2 ),..., p( xn ) в виде таблицы или графика распределения дискретной
СВ.
x1
x2
x3
x4
… xn
p3
p1
p2
p4
… pn
Такое представление называется распределением вероятностей
дискретной случайной величины  .
Для непрерывной случайной величины не удается ввести подобное
распределение вероятностей. Непрерывная случайная величина является
простейшей
моделью
непрерывного
случайного
процесса
(СП),
рассматриваемого в определенный момент времени.
Произвольная i -я реализация случайного процесса ( i ) (t ) имеет вид:
При этом x1 значение случайной величины 1 , являющейся выборочным
значением случайного процесса (i ) (t ) в момент времени t1 .
Универсальным как для дискретных, так и для непрерывных случайных
величин является понятие функции распределения вероятностей
(интегральной функции распределения):
10
F ( x )  P  x,
где символ PA означает вероятность возникновения положительного исхода
события A , т.е. вероятность того, что случайная величина   x .
Для непрерывной случайной величины F ( x ) функция распределения
будет непрерывная.
Для дискретной случайной величины функция распределения F ( x ) имеет
ступенчатый вид и может быть представлена следующим образом:
F ( x )   P  xk .
xk  x
Функция распределения обладает следующими свойствами:
1. F ( )  0;
2. F ( )  1;
3. F (x ) - неубывающая функция аргумента;
4. F ( x2 )  F ( x1 )  Px1    x2 
Плотность вероятности (дифференциальная функция распределения)
непрерывной случайной величины x может быть определена через функцию
распределения. Она имеет следующий вид
W ( x ) 
dF ( x )
11
dx
.
Для непрерывной случайной величины x функция W (x ) непрерывна.
Функция плотности вероятности позволяет найти вероятность того, что
непрерывная случайная величина принимает значения x1    x2 :
x2
Px1    x2    W ( x )dx .
x1
Для дискретной случайной величины аналогично можно записать:
W ( x )   P  xk ( x  xk ) ,
k
где (x ) – дельта-функция Дирака.
Плотность вероятности смешанной случайной величины  содержит как
непрерывную, так и дискретную части:
W ( x)  W( н) ( x)  W(д) ( x) ,

причем  W ( x )dx  1 – условие нормировки.

1.2.2. Числовые характеристики случайных величин
Основными числовыми характеристиками случайных величин являются
моменты распределения – начальные и центральные. Начальные моменты k го порядка (соответственно для непрерывных и дискретных величин) имеют
вид:

n
mk    x kW ( x )dx;
mk    P  xi xik .
i 1

Аналогично центральные моменты k -го порядка:

n
M k    ( xi - m1) W ( x )dx;
M k    P  xi ( xi  m1) k .
k
i 1

В частности, математическое ожидание (mean) и дисперсия (variance)
соответственно для непрерывной и дискретной случайной величины  равны:
12

m1   xW ( x )dx;


M 2    ( xi - m1) 2W ( x )dx;

n
m1   P  xi xi ;
i 1
n
M 2    P  xi ( xi  m1)2 .
i 1
Корень квадратный из второго центрального момента называется СКО
(standard deviation) M 2    и характеризует отклонение СВ от среднего
значения.
Корень квадратный из второго нецентрального момента называется
m2   2  m12{}  D и
отклонение (root mean square – RMS)
характеризует суммарную ошибку СВ. Например, инструментальную
(регулярную) и случайную ошибки измерения.
Кроме первого и второго моментов у СВ есть другие статистические
характеристики:
xм
1. Медиана
СВ,
для
которой
выполняется
условие
P{  xм }  P{  xм }  0,5 ;
2. Мода под которой понимается xmax максимальное значение плотности
распределения СВ P{  max }  Pmax .
Математическое ожидание (МО) имеет смысл среднего арифметического СВ.
p   p2 2  ...  pn xn
.
По определению имеем m1{}  1 1
p1  p2  ...  pn
МО обладает следующими свойствами:
1. m1{C}  C , где С  const ;
2. m1{C}  Cm1{} ;
3. m1{  }  m1{}  m1{} , где  и  СВ;
4. m1{}  m1{}m1{} для статистически независимых СВ.
СКО  СВ характеризует её отклонение от среднего значения (МО) m1{}.
СКО имеет размерность СВ и характеризует случайную ошибку измерения
СВ.
Квадрат СКО  2 называется дисперсия. Она обладает свойствами:
1. Для линейно зависимых СВ   C , где С  const справедливо
2  C 22 ;
2. Для
статистически
M 2{  }  2  2 ;
независимых
13
СВ

и

справедливо
3. Можно показать, что M 2{}  m2{}  m12{} .
Для симметричных относительно m1 распределений имеем:
M 2i 1  0,
где i  0,1,2,...
А для первого центрального момента выполняется условие:

M 1   ( x - m1)W ( x )dx  0 .

Для произвольного распределения M 3  третий нечетный момент,
характеризует асимметрию распределения относительно m1, может быть
представлен в нормированном виде
1 
M3
M 23
и называется
коэффициент асимметрии. Так, для нормального
распределения с математическим ожиданием a и дисперсией  2
 ( x  a )2 
1
 ,
W ( x) 
exp  
2
2
2



имеем M 3  0 и, следовательно, 1  0 .
Пусть случайная величина имеет распределение Релея, следующего вида
 x2 
x
W ( x )  exp   2  ,

 2 
где x  0 . Вид функции W (x ) – плотности вероятности распределения Релея
асимметричен относительного своего максимального значения. Расчет
коэффициента асимметрии дает значение 1  0,63 .
Иногда используют численную характеристику «остроты» кривой
распределения W (x ) около моды (максимального значения)
2 
M4
 3,
M 22
14
называемую
коэффициентом эксцесса. В частности, для нормального
распределения получаем  2  0 . В то же время для релеевского распределения
 2  0,23 .
Значения 1 и  2 часто используются, чтобы характеризовать степень
отличия анализируемого распределения от нормального.
1.2.3. Биномиальное распределение
Относится к дискретным распределениям случайной величины.
Вероятность того, что в последовательности из n независимых испытаний
некоторое событие A произойдет ровно k раз, равна
Pn (k )  Cnk p k (1  p) nk .
n
Из условий нормировки имеем  Cnk p k (1  p ) n  k  1 .
k o
Первый и второй моменты
m1{}  np; M 2 {}  np(1  p ) .
распределения
соответственно
равны
 (k  a )2 
1

exp  
Можно показать, что при p  const и n  1 Pn (k ) 
2
2
2



, распределение стремится к нормальному, где a  np; 2  np(1  p ) , причем
наибольшая точность достигается при стремлении значения p к величине
p  0,5 .
При описании потока редких событий с p  1, в последовательности
независимых испытаний, имеет место другое асимптотическое выражение
a
биномиального распределения.
Пусть
p  , n  1, p  1. Тогда
n
биномиальный закон распределения можно приближенно представить в
следующем виде
k
n k
a
ka 
Pn (k )  Cn   1   ,
n  n
a k ea
причем lim Pn (k ) 
.
n 
k!
Закон называется
распределение Пуассона. Это распределение
представляет и самостоятельный интерес как модель потока редких событий
(поток заряженных частиц, последовательность молниевых разрядов, поток
заявок на обслуживание, поток отказов радиоаппаратуры и т.д.).
15
1.2.4. Нормальное распределение
На практике часто приходится встречаться с нормальным законом
распределения случайных величин. В соответствии с центральной предельной
теоремой А.М. Ляпунова, плотность вероятности суммы независимых,
равномерно малых слагаемых при неограниченном увеличении их числа сколь
угодно близко приближается к гаусcовскому закону распределения.
Нормальный закон распределения непрерывной случайной величины 
имеет вид:
 ( x  m1)2 
1

W ( x ) 
exp  
2 M 2  
2M 2  
где m1 ( )  m – математическое ожидание, а M 2   2 – дисперсия случайной
величины.
На рисунке показан нормированный гауссовский закон распределения
плотности вероятности для m  0 , 2  1. Вычислить МО и дисперсию
нормального распределения можно с помощью замены переменной и

 x2 
табличного интеграла Пуассона  exp   dx  2 или связанного с ним

 2

 
интеграла Лапласа  exp  x 2 dx   .

Функция распределения гауссовского закона имеет вид:
 (   m) 2 
1 x
F ( x ) 
 exp   22 d .
2  


16
Для расчета вероятности попадания случайной величины в интервал значений
P     необходимо провести вычисление интеграла
 (   m) 2 
1 
P     
 exp  22 d .
2 


m
, имеем
Произведем замену переменой  

m

 2 
1
  m
m





P     
d


exp




,

 2


2   m







 2 
1 x
где функция  ( x ) 
exp   d

 2
2  


– интеграла вероятности. Она
обладает свойством (  x )  1  ( x ) . На практике вероятность попадания
случайной величины в заданный интервал P     можно вычислить через
табулированную интегральную функцию Лапласа:
 2 
1 x
( x ) 
 exp   2 d .
2 0


Интеграл вероятности, связан с табулированной интегральной функцией
Лапласа простым соотношением (см. приложение П). Для неё справедливо
соотношение ( x )  ( x )  0,5 .
1.2.5. Распределение Рэлея
Среди важных и часто встречающихся на практике распределений,
связанных с гаусcовским (нормальным), является распределение Релея.
Рассмотрим задачу нахождения распределения величины   12  22 , где
статистически
независимые
СВ
с
параметрами
1 ,2
17
m11  m12   0; M 2 1  M 2 2   2 . Выборочные значения СВ , 1 , 2
обозначим соответственно y , x1 , x2 .
Функция распределения F ( y ) величины y равна вероятности того, что
конец вектора с проекциями x1 и x2 не выйдет за пределы окружности радиуса
y  x12  x22 или
F ( y ) 
 W ( x1, x2 )dx1dx2 .
( 2)
x12  x 22  y
Двумерная плотность вероятности статистически независимых СВ имеет вид
W( 2 ) ( x1, x2 ) 
Перейдем к новым
соотношениями:
Тогда имеем:
 x12  x22 
1
.
exp  
2 
22
2



переменным
(, ) ,
x1   cos 
x2   sin 
связанным
с
исходными
.
 2  ( x1, x2 )
1 2 y
F ( y ) 
  exp   22  (, ) dd,
22 0 0


где якобиан преобразования равен
x1 x1
( x1 , x2 )
  cos    sin 


 .
x2 x2 sin   cos 
(, )
 
После вычислений функции распределения имеем
y
 2 
 2 
1 2 y
F ( y ) 
 d   exp   22 d    d exp   22  
22 0 0
0




 y2 
 1  exp   2 , y  0.
 2 
Вычислим плотность вероятности распределения Релея, как производную от
F ( y )
18
 y2 
 2 exp   2 , y  0 .
W ( y ) 
 2 
dy



График плотности вероятности для   1 имеет вид.
dF ( y )
y
Модальное y  yM значение W ( y ) определяется из уравнения
 y2 
 y2  y2
1
 2 exp   2   4 exp   2   0 ,
dy

 2 
 2  
Откуда y M   . Соответственно
1
.
W ( yM ) 
 e
Вычисления первого и второго моментов распределения Релея дают
следующие результаты

4 2
m1   ,
M 2  
 .
2
2
dW ( y )
1.2.6. Равномерное распределение
В типовых задачах статистической теории радиотехнических систем
часто рассматриваются радиочастотное колебание вида:
S (t )  A(t ) cos[0t  (t )   ],
где A(t ) и (t ) – детерминированные временные функции, 0 – несущая
частота колебания, а  – случайная начальная фаза. Обычно допускаются с
равной вероятностью любые значения начальной фазы  в пределах [0,2] . В
19
этом случае мы имеем дело с равномерно распределенной случайной
величиной  .
В общем случае плотность вероятности равномерного распределения
случайной величины в интервале [a, b] имеет вид:
 1
a xb
,
W ( x )   b  a
.
 0, x  a, x  b
Найдем первый и второй моменты (математическое ожидание и дисперсию)
равномерно распределенной случайной величины:
ab
(b  a ) 2
m1{} 
M 2 {} 
;
.
2
12
Функция распределения случайной величины имеет вид:
 0, x  a
 xa
F ( x)  
, a  x  b.

b
a

 1, x  b
Для равномерно распределенной фазы радиосигнала в интервале
0    2 можно получить:
20
1
,
0    2;
2
1 2
m1{} 
 xdx  ;
2 0
(2) 2
2
2
2
M 2 {}  m2 {}  m1 {} 
  .
3
3
W ( x) 
1.3. Статистическое оценивание параметров распределения
Одной из важных задач математической статистики является разработка
методов получения обоснованных выводов о массовых явлениях и процессах
на основании анализа результатов наблюдений и экспериментов. При этом
выводы относятся не к отдельным испытаниям, не к самой анализируемой
выборке, сколь велика бы она ни была, но распространяются на весь
изучаемый процесс или явление.
Пусть, например, имеется партия из N ( N  1) каких-либо приборов
(например, транзисторов), и необходимо, выбрав случайным образом
некоторое количество n  N из N и сделать вывод о качестве всей партии.
Вся совокупность изучаемых объектов или экспериментальных данных
называется генеральной совокупностью. Величина N – объем генеральной
совокупности.
Часть генеральной совокупности, наугад отобранная из нее, называется
случайной выборкой, или просто выборкой. Число n объектов (данных),
составляющих выборку, называется объемом выборки.
Обычно каждому i -му (при определенном порядке их расположения)
элементу выборки можно сопоставить определенное числовое значение xi .
Тогда выборку можно представить вектор-строкой ( x1 ,..., xn ) .
Это могут быть, например, значения реализации случайного процесса в
моменты t1 ,..., t n . Рассматриваемая выборка представляет собой реализацию
случайного вектора как совокупности случайных величин 1 ,..., n .
Используемая выборка более или менее удачно (в том или ином смысле)
характеризует изучаемые свойства генеральной совокупности. Существуют
так называемые репрезентативные выборки, которые наиболее хорошо (в
смысле того или иного критерия) представляют свойства генеральной
совокупности.
Далее, если не будет специальных оговорок, будем полагать
распределения W ( xi ) всех величин i одинаковыми, а сами величины
статистически независимыми, т.е.
21
W( n ) ( x1 ,..., xn ) 
n
W ( xi ) ,
i 1
где W ( xi ) не зависит от выборочного значения в момент ti , т.е. случайный
процесс является стационарным. Будем предполагать так же, что выполняется
условия эргодичности. Для таких процессов важнейшей является задача
оценки неизвестных параметров распределений генеральной совокупности.
1.3.1. Выборочное среднее
Первой задачей, которая часто возникает при статистическом анализе
имеющейся в наличии выборки, является попытка определения (оценки)
величины математического ожидания m1 ξ  генеральной совокупности. Будем
далее называть величину m1 ξ  – генеральным средним.
По существу, единственное, что удается сделать, это найти некоторую
статистическую оценку m̂1 генерального среднего m1 ξ .
Выберем в качестве такой оценки случайную величину  вида:
1 n ,
 i
n i 1
т.е. среднее арифметическое элементов выборки. Определенная таким образом
величина m̂1 называется выборочным средним. Значения x случайной
величины  равны
1 n
x   xi .
n i 1
Основными числовыми характеристиками случайной величины 
являются математическое ожидание m1 и дисперсия M 2 .
Имеем:
1 n  1 n
m1  m1   i    m1i   m1{}.
 n i 1  n i 1
Итак, математическое ожидание выборочного среднего совпадает с
генеральным средним, или выборочное среднее представляет собой
несмещенную оценку генерального среднего. Найдем дисперсию случайного 
среднего значения
1
1 n  1 n
M 2   M 2   i   2  M 2   M 2 ,
n
 n i 1  n i 1
где M 2  – дисперсия генеральной совокупности (генеральная дисперсия).
  mˆ 1 
22
Таким образом, с ростом объема выборки дисперсия выборочного
среднего стремится к нулю. В этом случае говорят, что выборочное среднее по
вероятности стремится к истинному генеральному среднему с увеличением
объема выборки. Такие оценки называются состоятельными. Итак,   m̂1
является несмещенной и состоятельной оценкой величины  .
Определим объем выборки n0 , требуемый для того, чтобы
среднеквадратическое отклонение
математического
M 2  оценки
ожидания m̂1 не превышало заданной величины  . Такую оценку m̂1
будем называть точечной. Для точечной оценки имеем:
M 2   .
Тогда для дисперсии генеральной совокупности получим:
M 2 
 .
n0
Необходимое количество выборочных значений удовлетворяет неравенству
M 
n0  22 .

Пусть, например,
   M 2 .
Тогда
1
n0  2 .

2
Так, для значения   10 имеем n0  104 .
Можно использовать и иную характеристику качества оценки  .
Определим вероятность того, что разность   m1   по модулю не
превосходит заданного значения  . Такую оценку будем называть
интервальной, поскольку она задает доверительный интервал.
Для этого необходимо знать распределение случайной величины  . Будем
считать, что при n  1 распределение величины   m̂1 близко к
нормальному. Тогда вместо неизвестных статистических параметров можно
поставить их оценки:

1
 ( x  mˆ 1)2 

W ( x ) 
exp 
.


M

2
2M 2 


2


Вероятность того, что оценка среднего значения случайной величины не
отличается от истинного значения на величину   равна:
23
P  m1   Pm1      m1   
Последний
m1  
 ( x  m1)2 
1

 exp   2 M  dx.


2M 2  m1  
2


интеграл может быть вычислен через
табулированную
t
1 0
t2
нормированную функцию Лапласа (t0 ) 
 exp(  2 )dt . Произведем
2 0
x  m1
замену переменной интегрирования t 
и, учитывая, что
M 2 
1
M 2   M 2  получим
n
  n 
.
P  m1   2



M

2


Так, для случая    M 2  имеем:




P   m1   M 2   2  n .
Так, для   102 и n  104 :
P   m1  10 2  102  2 1  0,68,


откуда видно, что объем n  104 выборки не является достаточным, поскольку
обеспечивает вероятность отклонения случайной величины от истинного
значения не более 68%. Обычно требуются оценки с вероятностями 95% или
99,7%.
Отсюда можно сделать вывод, что применение разных критериев оценки
случайной величины дают разные объемы выборочных значений.
1.3.2. Выборочная дисперсия
Для определения требуемого объема выборки при оценке генерального
среднего с заданной точностью, как было показано выше, необходимо знание
генеральной дисперсии M 2 . Кроме того, оценка величины M 2  может
представлять и самостоятельный интерес.
Выберем в качестве оценки M̂ 2  генеральной дисперсии M 2 
величину     вида:
2
   2  Mˆ 2   1  i   2 ,
n
n i 1
24
1 n
2
где    i  mˆ 1 – выборочное среднее. Величина     называется
n i 1
выборочной дисперсией. Значения случайной величины     равны:
2
2
1 n
 1 n 
x  x     xi    xk  .
n i 1 
 n k 1 
Точно так же, как и в случае выборочного среднего  , можно ввести в
2

рассмотрение математическое ожидание выборочной дисперсии m1    


2
дисперсию выборочной дисперсии Mˆ 2   M 2     .
Представим M̂ 2  в форме:
1 n
1 n 2
2
2
ˆ
M 2         i      i  2( )2  ( )2  2  ( )2 ,
n i 1
n i 1
где
1 n 2
2
   i .
n i 1
Найдем математическое ожидание выборочной дисперсии. Имеем:
1 n
2

 1 n n
2
2
2
m1      m1   m1 (  )   m1  m1  2   i  k  
n i 1

 n i 1 k 1
1 n
1
n2  n 2

2
2
2
2
 m2   2  m1 i  (n  n)m1   m2   m2  
m1  
n
n  i 1
n2

n 1
n 1

m2   m12  
M 2 .
n
n

  

 
 


Итак, окончательно имеем:


2
и
 
 n n 1 M . .
m1     
2
2
Таким образом, с увеличением объема выборки математическое ожидание
выборочной дисперсии стремится к генеральной дисперсии M 2 , однако при
любом конечном n , строго говоря, m1 Mˆ 2   M 2 . Следовательно,
рассматриваемая статистическая оценка дисперсии генеральной совокупности
является смещенной.
Иногда оказывается удобным пользоваться несмещенной оценкой
генеральной дисперсии. Рассмотрим величину:
n ˆ
Mˆ 2 H 
M 2 ,
n 1

25

где M̂ 2  – выборочная дисперсия. Тогда
n
n
2
m1 Mˆ 2 H 
m1 Mˆ 2  
m1      M 2 .
n 1
n 1
n
Таким образом, оценка Mˆ 2 H 
  2 является несмещенной
n 1
оценкой генеральной дисперсии. Видно, что при больших значений n  1 обе
оценки совпадают.
Аналогично получим формулу и для дисперсии выборочной дисперсии.
Можно показать, что при n  1:
1
2
2
M 2 Mˆ 2   M 2      M 4   M 22   2 M 4   2 M 22  
n
n
1
1
 3 M 4   3M 22   M 4   M 22  .
n
n
При увеличении объема выборки






 





 





lim M 2      0 .
n 
2
Таким образом, выборочная дисперсия     сходится по вероятности к
генеральной дисперсии M 2 , т.е. является состоятельной оценкой величины
M 2 .
В
частности,
для
гауссовской
генеральной
совокупности
2
2
M 4   3M 2 , M 2    , так что
n 1
2
M 2   2
m1 Mˆ 2   m     
n
3M 22   M 22  2 4
2
ˆ
M 2 M 2   M 2     
  .
n
n
Определим объем выборки nT , требуемой для того, чтобы СКО
отклонения МО от истинного значения не превышало значения  . Для этого
2










необходимо, чтобы выполнялось условие M 2 M̂ 2    .
Для гауссовской генеральной совокупности, это условие имеет вид
2 M 22 
  . Найдем необходимый объем выборочных значений для
n
выполнения точности определения СКО в виде точечной оценки. Положим
2
вместо неравенства знак равно   M 2 . Тогда получаем условие nT  2 .

2
Так, для уменьшения исходного СКО на величину   10
(в сто раз)
26
необходимо произвести вычисления для оценки значений МО и дисперсии для
nT  2  104 независимых выборочных значений.
1.4. Совокупность случайных величин
1.4.1. Функции распределения совокупности СВ
Под случайным процессом (СП) подразумевается бесконечная временная
реализация тока или напряжения случайным образом изменяющаяся во
времени (тепловой шум). Данный СП можно условно разделить на конечные
временные отрезки длительностью t  0, T  в виде бесконечного числа
статистически независимых реализаций, составляющих т.н. ансамль
реализаций СП.
Для полного описания случайного процесса (СП), конечно, не достаточно
иметь распределение вероятностей его значений лишь в один момент времени.
Обычно необходимо описывать взаимную зависимость значений СП на
интервале наблюдения t  0, T  в различные моменты времени t1 , t2 ,...., tn как
на приведенном ниже рисунке, где представлена произвольная i -я реализация
случайного процесса (i ) (t ) .
При этом можно говорить о совокупности случайных величин
1  (t1 ), 2  (t2 ),..., n  (tn ) как более сложной и адекватной модели СП. В
этом случае необходимо перейти к рассмотрению (t ) многомерного
принимающего выборочные значения
случайного n -мерного процесса,
x( x1 ,..., xn ) в моменты времени (t1 ,...., tn ).
Вероятность того, что при этом для всех выборочных значений Pi  xi 
для всех 1  i  n выполняется одновременно
F( n ) x,1 , x2 ,..., xn , t1 , t2 ,....,tn   P1  x1 , 2  x2 ,..., n  xn 
называется n -мерной функцией распределения вероятностей случайного
процесса (t ) , или совокупности случайных величин 1 ,..., n .
Очевидно, что n -мерная функция распределения обладает свойством
F ( xi )  F( n ) (,...,, xi , ,...,) ,
27
где  - знак бесконечно большого значения аргумента.
Если
F( n )  x1 ,..., xn    F ( xi ) ,
n
i 1
n
где  Fi  x  – обозначение операции произведения функций, то случайные
i 1
величины 1 ,..., n называются статистически независимыми.
Производная n -го порядка от функции распределения
 n F( n ) x ( n )
(n)
(n)
W x 
x1 ,..., xn
называется n -мерной плотностью вероятностей случайного вектора ξ (n ) ,
или совокупности случайных величин 1 ,..., n .
Соответственно n -мерная функция распределения связана с n -мерной
плотностью вероятности соотношением

 
F( n ) ( x1 ,..., xn ) 
x1
xn


(n)
 ...  W ( x1 ,..., xn )dx1...dxn ,
откуда следует условие нормировки:
F( n ) ( ,..., ) 





(n)
 ...  W ( x1 ,..., xn )dx1...dxn  1 .
Для статистически независимых величин, очевидно, имеем
n
W( n ) ( x1 ,..., xn )  W ( xi ) .
i 1
i
Многомерная функция плотности вероятности обладает свойством
согласованности:




W ( x1 ,..., xm )   ...  W ( x1 ,..., xm ,..., xn )dxm 1    dxn .
Тогда для любой многомерной плотности вероятности W( n ) ( x1,...,xi ,...,xn )
можно получить одномерную плотность вероятности путём интегрирования по
соответствующим аргументам.
1.4.2. Условные плотности вероятности многомерного СП
Пусть имеется двумерный случайный процесс 1 ,2 , заданный
плотностью вероятности W ( x1 , x2 )
со статистически зависимыми
выборочными значениями в моменты времени t1 ,t2 . Для него можно ввести
условную плотность вероятности случайной величины 1 , принимающей
28
значение x1 относительно случайной величины  2 , принимающей значение x 2
в виде:
W( 2 ) ( x1, x2 )
W ( x1 / x2 ) 
,
W ( x2 )

где W ( x2 )   W( 2 ) ( x1 , x2 )dx1 одномерная плотность вероятности случайной

величины  2 . Условная плотность вероятности W ( x1 / x2 ) содержит больший
объем информации, чем одномерная плотность вероятности W ( x1 ) .
Условная плотность вероятности W ( x1 / x2 ) имеет следующие свойства:

1. Свойство нормировки  W ( x1 / x2 )dx1  1 ;

2. Для статистически независимых случайных величин 1 и 2
справедливо W( 2) ( x1, x2 )  W ( x1 ) W ( x2 ) . Тогда для условной плотности
вероятности имеем W ( x1 / x2 )  W ( x1 ) .
3. Пусть случайные величины связаны между собой детерминированной
зависимостью 1  g ( 2 ) . Тогда двумерная плотность вероятности случайных
величин может быть выражена через одномерную плотность вероятности
вида:
W( 2 ) ( x1 , x2 )  W ( x2 )( x1  g ( x2 )) ,
где (x) – дельта-функция Дирака.
4. Формулы двумерной условной плотности вероятности случайных
величин 1 и  2 могут быть обобщены на n -мерную плотность распределения:
W( n 1) ( x1 ,..., xn 1 )
( n 1)
.
W ( x1 ,... xn 1 / xn ) 
W ( xn )
1.4.3. Числовые характеристики совокупности СВ
В общем случае введём смешанные начальный и центральный моменты
порядка ( k1 ,..., kn ) совместного распределения совокупности случайных
величин:


mk ...k 1 ,...,  n    ...  x1k ...xnk W( n ) ( x1 ,..., xn )dx1 ...dxn  x1k ...xnk  .
1
1
n

n
1

n
Операция    обозначает усреднение выборочных значений по ансамблю
реализаций случайных величин. В дальнейшем    будет пользоваться для
более компактного обозначения операции статистического усреднения.
29




M k1 ...k n 1 ,..., n    ...  [ x1  m11]k1 ...[ xn  m1n ]k n W( n ) ( x1,..., xn )dx1...dxn .
Отсюда легко получить любые начальные и центральные моменты k - го
порядка для каждой i :




mk1 i    ... 




M k1 i    ...  xi  mi i 
k1
xik1W( n ) ( x1 ,..., xn )dx1...dxn 
W( n ) ( x1 ,..., xn )dx1...dxn 

 xi 1W ( xi )dxi ;
k


 [ xi  m1xi ] 1 W ( xi )dxi .
k

Одной из важнейших характеристик совокупности случайных величин
является смешанный центральный момент первого порядка:
 
M 11 i ,  j     [ xi  m1 i ][ x j  m1  j ]W( 2) ( xi , x j )dxi dx j  Rij .

Он представляет собой матрицу корреляции R размера (n  n) выборочных
значений случайных величин i и  j , состоящих из коэффициентов Rij .
Аналогичные соотношения для не центрированных случайных величин
i и  j из значений m11 i ,  j   kij образуют k матрицу ковариации.
Корреляционный и ковариационный коэффициенты матриц связаны простым
соотношением:
 
Rij    xi x jW( 2 ) ( xi , x j )dxi dx j  m1{i }m1{ j }  kij  m1{i }m1{ j }.
 
Нормированные значения коэффициентов матрицы корреляции
rij 
Rij
M 2 { i }M 2 { j }
называются коэффициентами корреляции случайных величин i и  j .
В частности, для статистически независимых случайных величин i и  j
имеем:
 
Rij    xi x jW ( xi )W ( x j )dxi dx j  m1{ i }m1{ j } 
  
 m1{ i }m1{ j }  m1{ i }m1{ j }  0.
Rij  0 ,
Случайные
величины,
для
которых
называются
некоррелированными.
Итак, статистически независимые случайные величины являются
некоррелированными. Обратное утверждение в общем случае неверно.
30
Рассмотрим физический смысл понятия корреляции случайных величин.
Для этого перейдем от величин i к центрированным и нормированным
случайным величинам i вида:
  m1{ j }
  m1{i }
,
;
j  j
i  i
M 2 {i }
M 2 { j }
принимающим значения xi и x j соответственно. Введем в рассмотрение
неотрицательную величину
 
L    ( xi  x j ) 2 W( 2 ) ( xi , x j )dxi dx j 
 
.
 


  ( xi ) W ( xi )dxi   ( x j ) W ( x j )dx j  2   ( xi x j )W ( xi , x j )dxi dx j
2
2
Нетрудно
 


видеть,
что
( 2)

L  2(1  rij )  0 . Отсюда следует, что модуль
коэффициента корреляции всегда rij  1 .
Определим значение L для rij  1 . Тогда используя выражение, для
величины L с отрицательным знаком в подынтегральном выражении,
получаем L  0 . Но это значит, что для всех значений величин i и  j
выполняется xi  x j , т.е. i   j , или
i 

M 2 {i }
M 2 {i } 
M 2 {i }
(  j  m1{ j })  m1 {i }   j
 m1{i } 
m1{ j },

M 2 { j }
M 2 { j } 
M 2 { j }

откуда получаем линейную зависимость для случайных величин i  a j  b .
Аналогично, для rij  1, используя запись L с положительным знаком в
подынтегральном выражении, получаем xi   x j или i    j , так что
i  a j  b . Итак, условие rij  1 означает линейную зависимость случайных
величин i и  j .
Рассмотрим в качестве примера двумерное нормальное распределение
двух нормально распределенных коррелированных случайных величин с
коэффициентом корреляции r . Двумерная плотность вероятности случайных
величин имеет вид
W( 2 ) ( x1 , x2 ) 
1
212

 ( x1  a1 ) 2
1
( x1  a1 )( x2  a2 ) ( x2  a2 ) 2  

r


exp
2

 ,
2
2
2 

r




2
(
1
)
1  r2
2
1 2
1



где a1  m1{1}, a2  m2{2 }, 12  M 2{1}, 22  M 2{2 }.
Можно показать, что функция взаимной корреляции и коэффициент взаимной
корреляции в наших обозначениях равны
31
R12  r1 2 , r12  r.
Для некоррелированных нормальных величин r  0 . Из общего
выражения имеем:
  ( x1  a1 )2 ( x2  a2 )2  
1
( 2)

W ( x1, x2 )  W ( x1 )W ( x2 ) 
exp  
 .
2
2
212


2
2
1
2

 
Отсюда следует важное свойство: некоррелированность нормальных
случайных величин означает также и их статистическую независимость.
1.4.4. Стационарные СП
Случайный процесс стационарен в узком смысле, если выполняется
условие
W( n ) ( x1, x2 ,..., xn , t1, t2 ,...,tn )  W( n ) ( x1, x2 ,..., xn , t1  , t2  ,...,tn  ) .
Это означает, что статистические характеристики и функции СП ведут себя
неизменно во времени.
Для одномерной плотности вероятности СП получим отсутствие
временной зависимости W(1) ( x1, t1 )  W(1) ( x1 ) .
Для двумерной плотности вероятности СП при t2  t1   имеем
W( 2) ( x1, x2 , t1, t2 )  W( 2) ( x1, x2 , ) зависимость от разности   t2  t1 .
Найдем первые два момента стационарного в узком смысле СП.
Математическое
ожидание

M 1{}   xW ( x)dx  m
и
дисперсия


M 2 {}   ( x  m) 2 W ( x)dx   2 не зависят от времени. Автокорреляционная

функция (АКФ) СП равна:
 
M 11{i ,  j }    ( xi  m)( x j  m)W( 2 ) ( xi , x j , )dxi dx j  kij ()  m 2  Rij () ,
 
где   t j  ti – зависит от разности временных отсчетов выборочных
значений.
Если условие стационарности выполняется только для первых двух
моментов СП, то такой процесс называется стационарным в широком смысле.
Из стационарности в узком смысле следует стационарность в широком
смысле, но не наоборот.
Поскольку гауссовский СП имеет отличные от нуля только первый и
второй моменты, то для него условия стационарности в широком и узком
смысле совпадают.
Перечислим основные свойства АКФ стационарного СП:
32
1. АКФ является четной функцией аргумента R()  R() ;
2. Максимальное значение АКФ равно R(0)   2 ;
R()  0 ;
3. АКФ монотонно убывающая функция lim

4. Необходимое и достаточное условие существования АКФ является
выполнение соотношения

 R() cos d  0 .
0
R()
, откуда
2
следует, что  1  r ()  1 . Для характеристики корреляционных свойств СП
вводят время корреляции

1 
 k   r ()d   r ()d .
2 
0
Время корреляции  k составляет характерный временной интервал
изменения значений стационарного СП.
Коэффициент корреляции стационарного СП равен r () 
1.4.5. Эргодические СП
Ранее предполагалось, что выборочные значения многомерного
случайного
процесса
представляют
собой
случайные
величины,
статистические характеристики которых можно получить путем усреднения
выборочных значений в данный момент времени по ансамблю временных
реализаций. В реальной деятельности это практически невозможно.
Сделаем допущение о возможности получения статистических
характеристик для стационарного случайного процесса на достаточно длинном
временном интервале путем усреднения выборочных статистически
независимых значений. Такое усреднение можно назвать усреднением во
времени. Если статистические характеристики стационарного СП полученные
усреднением по ансамблю и по времени совпадают, то такой СП будет
называться стационарным и эргодическим. Необходимым и достаточным
R()  0 .
условием эргодичности является выполнение условия lim

Оценку МО, дисперсии и АКФ стационарного и эргодического СП на
временном интервале t  [0, T ] можно получить в следующем виде:
T
1
ˆ
mT  lim
 (t )dt – оценка МО;
T T  0
T
1
2
ˆ T  lim
 [(t )  m]dt – оценка дисперсии;
T T  0
33
1
RˆT ()  lim
 [(t )  m][(t  )  m]dt – оценка АКФ.
T T  0
Выражения позволяют для достаточно большого временного интервала
получить оценку статистических характеристик стационарного и
эргодического СП.
T
1.4.6. Спектральные характеристики СП
Спектральные характеристики стационарного и эргодического СП могут
быть получены по теореме Винера-Хинчина, как Фурье преобразование его
АКФ:

G()   R() exp( j)d – энергетический спектр СП;

1 
R() 
 G() exp( j)d – АКФ СП.
2  
Из последнего выражения можно получить дисперсию СП по формуле
Парсеваля:
1 
2 
 G ()d .
2  
Видно, что энергетический спектр СП G () характеризует распределение
мощности процесса в заданной полосе частот [,   d] . Поэтому G () носит
название спектральная плотность мощности СП.
Поскольку АКФ является четной функцией своего аргумента, то для
энергетического спектра и АКФ имеем:

1 
G()  2  R() cos d и R()   G () cos d .
0
0
Реальный энергетический спектр имеет смысл только для области
положительных частот, тогда выражения можно представить в следующем
виде:

G( f )  4  R() cos 2fd ,
0

R()   G( f ) cos 2fdf ,
0
где f  0 – частота энергетического спектра, а
G(2f )  G()  G( )  2G() .
34
1.4.7. Плотность вероятности гауссовского СП
1. Пусть имеется n-мерный гауссовский СП (t ) , представленный своими
выборочными значениями ( x1 , x2 ,..., xn ) на интервале наблюдения t  [0, T ] с
T
временным интервалом дискретизации t  ti  ti 1 
. Многомерный
n 1
гауссовский СП имеет отличные от нуля только первый и второй моменты.
Тогда многомерная плотность вероятности такого процесса может быть
представлена в следующем виде:
W( n ) ( x1 , x2 ,..., xn ) 
 1 n D

1

,


(
)(
)
exp
R
x
m
x
m

ij
i
i
j
j 
n

(2) R
 2 R i , j 1

12 R12 ... R1n
R21  22 ... R2n
где R 
– определитель
...
... ... ...
Rn1 Rn 2 ...  n2
корреляции n-мерного СП для которого Rij  R ji ;
симметричной
матрицы
mi  xi  – математическое ожидание СВ;
i2  ( xi  mi ) 2  – дисперсия СВ;
RijD
–
алгебраическое
дополнение
определителя
R,
полученное
произведением ( 1)i  j на определитель R с вычеркнутыми i-ой строкой и j-м
столбцом.
Многомерная плотность вероятности гауссовского случайного процесса
может быть представлена в компактной векторно-матричной записи.
1
 ( X  m) T R 1 ( X  m) 
exp  
W ( X) 
,
2
(2) n R


где X и m вектор-столбецы выборочных значений гауссовского процесса и
математического ожидания выборочных значений;
матрица R 1 - обратная матрица для матрицы корреляции R . Она может быть
получена путем транспонирования коэффициентов матрицы R так, что
справедливо R  R 1  1 . Коэффициенты матрицы R 1 могут быть получены из
D
1
i  j Rij
выражения: Rij  (1)
.
R
35
2. Плотность вероятности n-мерного стационарного гауссовского СП
(t ) может быть представлена в векторно-матричной записи. Для плотности
вероятности с нулевым математическим ожиданием имеем:
1
 XT R 1 X 
W ( X) 
exp  
,
2 
(2) n R

 2 R12 ... R1n
R21  2 ... R2 n
– определитель
где R 
...
... ... ...
Rn1 Rn 2 ...  2
корреляции n-мерного СП для которого Rij  R ji ;
2 – дисперсия СВ.
Можно показать,
что
в
результате
симметричной
матрицы
выполнения
операции
n
XT R 1 X   ( Rij1 ) xi x j – является скаляром (числом).
i , j 1
3. Рассмотрим частный случай n-мерного стационарного гауссовского
СП (t ) с некоррелированными временными отсчетами. Пусть статистические
N
характеристики такого процесса равны m  0, 2  0 , где N 0  const –
2t
спектральная плотность мощности СП в полосе 1герц. Для одномерной
плотности вероятности i-го отсчета СП имеем:

1
 xi2 t 
1
 xi2   N 0  2
 .
W ( xi ) 
exp   2   
 exp  
N
2
 2   t 

0 
Поскольку отсчеты не коррелированы, то для n-мерной плотности вероятности
можно записать:
n
n
 

xi2 t 
n
2


N


W ( x1 ,..., xn )   W ( xi )   0  exp   i 1
.
i 1
N
 t 
0




Рассмотрим предельный случай при t  0, n  . Многомерная плотность
вероятности СП переходит в функционал плотности вероятности:
1 T 2

W ( x(t ))  C exp   x (t )dt  ,
 N0 0

где C  const , определяется из условия нормировки.
Модель данного СП представляет собой «белый» гауссовский шум.
Сколь угодно близко расположенные отсчеты такого шума не коррелированы,
36
N0
(t ) , где (t ) – дельта функция Дирака. Энергетический спектр
2

N
такого шума равен G ()   R() exp(  j)d  0 .
2

или R() 
Мощность такого шума  2  N 0 t   , что означает математическую модель
нереализуемую на практике.
Приближением к такой модели в радиотехнике является «тепловой»
шум, вызванный хаотическим движением электронов в проводнике. Известно,
что спектральная плотность мощности напряжения теплового шума на
сопротивлении R , в соответствии с формулой Планка, равна:
hf
kT
G ( f )  4kTR
,

 hf  
 exp    1
 kT  

где k  1,38  10 23 дж град – постоянная Больцмана;
T – температура в градусах Кельвина T  2730  t , t температура в градусах
Цельсия;
h  6,62  1034 дж  сек – постоянная Планка;
f – частота в герцах.
hf
При выполнении условия
 1, что справедливо для частот вплоть до
kT
f  300ГГц,   1мм , представленное выражение переходит в формулу
Найквиста:
G ( f )  4kTR  N 0 .
Найдем мощность шума на входе радиоприемного устройства при
идеальном П-образном по частоте входном фильтре НЧ с f  [0, F ] без
потерь.
37
Максимальное согласование источника теплового шума и входа приемника
достигается при выполнении условия R  RВХ .
Средняя мощность теплового шума в рабочей полосе приемника, равна
2
UШ
 2  4kTRF .
На входном сопротивлении приемника выделяется часть мощности
U Ш2
источника равная PВХ 
Для T  2900 , F  1мгц мощность
 kTF .
4 RВХ
входного теплового равна PВХ  4 1015 вт .
1.5. Воздействие СП на линейные системы
Линейной,
называется
система,
осуществляющая
линейные
преобразования входных сигналов. В такой системе справедлив принцип
суперпозиций, заключающийся в том, что сумма входных воздействий может
быть найдена путем суммирования откликов по каждому из воздействий в
отдельности. Для анализа процессов в таких системах используются методы:
решения дифференциальных уравнений, импульсных и переходных
характеристик (интеграл Дюамеля), метод преобразования Фурье и Лапласа и
другие.
Пусть имеется линейная система с передаточной функцией K ( j) на
входе которой поступает стационарный случайный процесс (t ) с известными
статистическими характеристиками m  0 и АКФ R () .
Необходимо найти статистические характеристики случайного процесса
(t ) на выходе линейной системы.
Известно, что передаточная и импульсная характеристики в линейной
системе связаны прямым и обратным преобразованиями Фурье:
38
1 
g (t ) 
 K ( j) exp( jt )d – импульсная характеристика линейной
2  
системы (фильтра);

K ( j)   g (t ) exp(  jt )dt – передаточная функция системы.

Будем предполагать, что g (t )  0, при t  0 линейная система устойчива, так,
что при воздействии дельта импульса на её входе lim g (t )  0 .
t 
Входной процесс (t ) можно представить через его спектральную
характеристику:

S ( j)   (t ) exp(  jt )dt ,
(1. 1)

1 
(t ) 
(1.2)
 S ( j) exp( jt )d .
2  
Для процесса на выходе фильтра имеем:
1 
(t ) 
(1.3)
 S ( j) K ( j) exp( jt )d .
2  
Перейдем от отдельной реализации к ансамблю реализаций, проведя
статистическое усреднение полученных выражений по ансамблю   
выражения (1.3). Меняя местами операции интегрирования и статистического
усреднения, имеем:
1 
 (t ) 
  S ( j)  K ( j) exp( jt )d  0 , поскольку
2  

 S ( j)    (t )  exp(  jt )dt  0 .

Таким образом, спектральная характеристика СП при сделанных
допущениях в установившемся режиме (без учета начальных условий и
переходных процессов в системе) является случайной величиной,
математическое ожидание которой равно нулю.
Найдем АКФ процесса на выходе фильтра. Из (1.3) имеем:
1 
(t  ) 
(1.4)
 S ( j) K ( j) exp( j(t  ))d
2  
Поскольку (t ) функция вещественная, то выражение (1.4) не изменится, если
в правой его части перейти к комплексно-сопряженным спектральным
характеристикам:
39
1  
(t  ) 
S ( j) K  ( j) exp(  j(t  ))d .

2  
Используя выражения (1.4) и (1.5), имеем:
R ( )  (t )(t  ) 
(1.5)
.
1  






S
(
j

)
S
(
j

)

K
(
j

)
K
(
j

)
exp(

j


)
exp[
j
(



)
t
]
d

d

  

4    
Учтем, что входной случайный процесс (t ) стационарен, а случайные
спектральные характеристики статистически независимы и имеют
 - коррелиров анную АКФ:
(1.6)
 S ( j)S ( j)  2G()(  ) ,
где G () - энергетический спектр случайного процесса (t ) . Подставим
выражение (1.6) в интегральное выражение и учитывая фильтрующее свойство
 -функции, получим:
1 
2
R ( ) 
G ( ) K ( j) exp(  j)d .
(1.7)

2  
Из выражения (1.7) видно, что энергетические спектры входного и
выходного случайного процесса в установившемся режиме связаны
соотношением:

2
G ( )  K ( j)  G ( ) .
(1.8)
Соотношение (1.8) позволяет найти связь спектральных характеристик
входного и выходного процессов в частотной области. Определим связь АКФ
входного и выходного случайных процессов.
2
Определим Фурье-преобразование от K ( j) . Имеем:

K ( j)   g (t ) exp(  jt )dt

.

K  ( j)   g (t ) exp( jt )dt 

Найдем квадрат модуля передаточной функции фильтра:

 
K ( j) K ( j)    g (t ) g (t ) exp[  j(t  t )]dtdt  .
 
Сделаем замену переменной   t  t , имеем:
 


2

K ( j) K ( j)  K ( j)     g (t ) g (t   )dt  exp(  j)d .

   
40
(1.9)
Функцию в выражении (1.9) в фигурных скобках можно назвать АКФ
импульсной характеристики фильтра:

Rg ()   g (t ) g (t   )dt  .
(1.10)

Возьмем от выражения (1.9) от левой и правой части преобразование
Фурье и с учетом соотношения (1.10) получим:




R (t )  R (t )  Rg (t )   R ( ) Rg (t  )d   Rg ( ) R (t  )d ,
(1.11)
где  - обозначение операции временной свёртки.
Выражения (1.8) определяет связь СП на входе и выходе линейной
системы в частотной области в установившемся режиме. Выражение (1.11)
связывает входной и выходной СП без учета переходных процессов.
1.6. Нелинейное безынерционное преобразование СП
1.6.1. Функциональное преобразование совокупности СВ
Пусть задана совместная плотность вероятности W( n ) ( x1,..., xn )
непрерывных случайных величин 1 ,..., n . Пусть также задана совокупность
однозначных непрерывных функций yi  f i ( x1 ,..., xn ) n переменных,
определяющая связь значений
x1 ,..., xn случайных величин
1 ,..., n
со
значениями y1 ,..., yn новых случайных величин 1 ,..., n , так что
 1  f1 ( 1 ,..., n )

(1.12)
 .......... .......... ...... .
  f (  ,...,  )
 n
n 1
n
Такое преобразование будем называть нелинейным безынерционным
преобразованием. Необходимо определить совместную плотность вероятности
W( n ) ( y1,..., yn ) .
Начнем с рассмотрения одномерного случая. Пусть имеется случайная
величина  с распределением W (x ) . Задана функция y  f (x ) , определяющая
связь значений у новой случайной величины  со значениями x величины  .
При этом  определяется как   f () . Предположим, прежде всего, что связь
 и  однозначная, то есть существует однозначная и непрерывная функция
  () . Вероятности нахождения случайных величин связана соотношением:
P{ y0    y0  dy}  P{x0    x0  dx} ,
где y0  f ( x0 ) .
41
Последнее соотношение эквивалентно:
W ( y )dy  W ( x )dx .
Учтем взаимную связь y  f (x ) и обратное соотношение x  ( y ) .
Тогда для связи плотностей вероятностей имеем:
dx
d( y )
.
(1.13)
W ( y )dy  W ( x )
 W [( y )] 
dy
dy
Абсолютное значение производной связано с тем, что функции W ( y ) и
W (x ) не отрицательны.
Пусть теперь функция x  ( y ) неоднозначна и имеет l ветвей. В этом
случае выходной случайной величине y    y  dy соответствует одно из входных
значений xi    xi  dx , для i  1,2,..., l .
На рисунке представлен частный случай квадратичной зависимости l  2
.
В этом случае выражение (1.13) можно представить в обобщенном виде:
l
d ( y )
,
(1.14)
W ( y )  W [i ( y )]  i
dy
i 1
где значения i ( y ) и
di ( y )
соответствуют i-той ветви неоднозначной
dy
функции.
Полученный результат можно обобщить на случай n-мерной плотности
вероятности. Будем предполагать, что для системы преобразования (1.12) есть
набор взаимно однозначных преобразований вида:
 1  1 ( 1 ,..., n )

(1.15)
 .......... .......... ...... .
   (  ,...,  )
 n
n
1
n
По аналогии с ранее полученным выражением имеем:
W( n ) ( y1,..., yn )  W( n ) (1 ( y1,... yn ),...,n ( y1,... yn )) Dn ,
где Dn - якобиан преобразования случайных величин ( 1 ,..., n ) в ( 1 ,..., n ) :
42
1
y1
 ( 1 ,..., n )
Dn 
 ...
 ( 1 ,..., n ) n
y1
1
yn
... ... .
n
...
yn
...
В случае, если обратные функции (1.15) неоднозначные и имеют l ветвей
неоднозначности, необходимо осуществлять суммирование по каждой из
ветвей вида (1.14).
1.6.2. Функциональные преобразования двух СВ
Пусть известна плотность вероятности W( 2) ( x1, x2 ) . Необходимо найти
W( 2) ( y1, y2 ) , при известной функциональной зависимости:
1  1
.

f


(

,

)
 2
1 2
Пусть обратная функция 2  ( 1 , 2 ) известна и однозначна. Тогда
якобиан преобразования от ( x1 , x2 ) к ( y1 , y2 ) имеет вид:
1
0
( x1 , x2 ) ( y , y ) ( y , y )

1 2
1 2 .
( y1 , y2 )
y1
y2
Для двумерной плотности вероятности после преобразований имеем:
( y1 , y2 )
W( 2 ) ( y1 , y2 )  W( 2 ) ( y1 , ( y1 , y2 )) 
.
y2
Тогда для одномерной плотности вероятности нелинейного преобразования
имеем:


( y1 , y2 )
( 2)
dy1 . (1.16)
W ( y2 )   W ( y1 , y2 )dy1   W( 2 ) ( y1 , ( y1 , y2 )) 
y2


Выражение (1.16) позволяет найти на выходе устройства плотности
вероятности при нелинейных преобразованиях на входах для: суммы,
разности, произведения и частного двух входных случайных процессов 1 и  2
при известном совместном распределении W( 2) ( y1, y2 ) .
Рассмотрим несколько важнейших частных случаев. Из (1.16) получим:

1. Для суммы 2  1  2 , имеем W2 ( y2 )   W( 2 ) ( y1 , y2  y1 )dy1 ;

43

2. Для разности 2  1  2 , имеем W2 ( y2 )   W( 2 ) ( y1 , y2  y1 )dy1 ;


3. Для произведения 2  1  2 , имеем W2 ( y2 )   W( 2) ( y1 , y2 / y1 )

dy1
;
y1

4. Для частного 2  1 / 2 , имеем W ( y2 )   W( 2 ) ( y1 , y2  y1 )  y1  dy1 .
2

Для статистически независимых входных процессов имеем:
W( 2) ( y1, y2 )  W1 ( x1 ) W2 ( x2 ) .
Подставляя в полученные выражения соответствующие распределения,
можно получить статистические характеристики выходных процессов.
1.6.3. Преобразование декартовых координат в полярные
Пусть ( 1 , 2 ) – случайные декартовые координаты некоторой точки
( x1 , x2 ) (конца вектора) на плоскости. Задано распределение W( 2) ( x1, x2 ) .
Пусть входные процессы ( 1 , 2 ) статистически независимы, имеют
гауссовское распределение с параметрами m1  a; m2  b; 1  2   .
Необходимо найти совместную плотность вероятности W( 2) ( y1, y2 ) значений
случайных величин ( 1 , 2 ) вида
1  12  22 ,
1  0;
.
2  arctg 2 1, 0  2  2
Обозначим значения случайных величин ( 1 , 2 ) соответственно (, ) ,
вместо ( y1 , y2 ), как это обычно принято при переходе к полярным
координатам. Декартовы координаты связаны с полярными следующими
нелинейными соотношениями
x1    cos 
.
x2    sin 
Якобиан преобразования имеет вид:
( x1, x2 ) cos    sin 

 .
sin   cos 
(, )
Тогда
и
для
статистически
W( 2) (, )    W( 2) ( cos,  sin )
независимых входных процессов имеем W( 2) (, )    W1 ( cos )  W2 ( sin ) .
Заметим, что случайные величины ( 1 , 2 ) в последнем случае не
являются статистически независимыми.
44
Для одномерных распределений модуля  и фазы  вектора ( x1 , x2 ) в
общем случае имеем:
2
W1 ()    W( 2 ) ( cos ,  sin )d – для начальной фазы;
0

W2 ()   W( 2 ) ( cos ,  sin )d – для огибающей процесса.
0
Для двумерной плотности вероятности имеем:
 ( x1  a )2  ( x2  b)2 
1
( 2)
W ( x1, x2 ) 
exp 
.
2
22
2



Перейдем к полярной системе координат и получим:
 ( cos   a )2  ( sin   b)2 

( 2)
W (, ) 
exp 
.
2

2
22


Одномерное распределение огибающей  выходного процесса равно:
 2
 1
2
2 
W () 
exp
 2 ( cos   a )  ( sin   b) d 

2
2 0
 2

.
 2  a 2  b2  2 



exp  

  exp  2 ( a cos   b sin )d
2
22
2




0
Обозначим Z  a 2  b2 ;   arctg b a , тогда имеем:
 2  Z 2   Z 

I
W ()  2 exp 
,
(1.17)
2  0 2 



2




2
1
где I 0 ( x ) 
 expx  cos(  )d – модифицированная функция Бесселя
2 0
нулевого порядка. Распределение (1.17) называется распределением РелеяРайса, или обобщенным релеевским.


45
В частном случае a  b  0 имеем Z  0 и распределение переходит в
распределение Релея.
 2 

W ()  2 exp   2  .

 2 
Можно показать, распределение Релея-Райса характеризует одномерное
распределение огибающей суммы детерминированного сигнала и нормального
шума на выходе линейного детектора.
1.7. Примеры
1.7.1. Теория вероятности
Пример 1
Однотипная продукция с браком разложена в три одинаковых ящика. В
первом ящике брака 4 из 100 штук, во втором 6 из 120 штук, в третьем 8 из 80
штук. Из одного из ящиков равновероятно берется одна деталь. Чему равна
вероятность P( A) того, что она окажется бракованной?
Пусть P ( H 1 ) - вероятность того, что деталь взята из 1-го ящика, P( H 2 ) из второго, P ( H 3 ) из третьего. По условию задачи эти события
равновероятны:
P( H1 )  P( H 2 )  P( H 3 )  1 .
3
46
Условные вероятности события P A  равны:
 Hi 
, P A   6
, P A   1 .
P A   4
10
100
120  H 3 
 H1 
 H2 
Тогда полная вероятность искомого события равна:
3
1
 0,063(3) .
P( A)   P( H i ) P A   1  1  1  19
20 10
300
H i  3 25

i 1


Пример 2
На производстве работают три автоматических линии, выпускающие
качественные изделия с вероятностями: p1  0,9; p2  0,95; p3  0,8 . Первая
линия дает 50% продукции, вторая 30%, третья 20%. Определить вероятность
того, что наугад выбранное качественное изделие сделано на первой, второй
или третьей линии?
Пусть событие A состоит в том, что выбранное изделие качественное.
Пусть P ( Bi ) – вероятность того, что изделие сделано на i -ой линии. По
P( B1 )  0,5; P( B2 )  0,3; P( B3 )  0,2 .
условию
задачи
обозначим:
Соответственно условная вероятность того, что выбрано качественное изделие
iс
ой
линии
равны
соответственно:
Тогда
апостериорную
P A   0,98; P A   0,95; P A   0,8 .
 B1 
 B2 
 B3 
вероятность того, что качественное изделие сделано на i - ой линии по
P A 
Bi 
B
формуле Байеса равно: P i   P( Bi )  
. Для вероятности события A
 A
P( A)
P( A)   P( Bi )P A   0,5  0,98  0,3  0,95  0,2  0,8  0,935.
 Bi 
i 1
Подставим найденные значения в формулу Байеса:
1.
Для
качественного
изделия
с
первой
линии
0,98
P B1   0,5 
 0,524 ;
 A
0,935
2.
Для
качественного
изделия
со
второй
линии
0,95
P  B2   0,3 
 0,305 ;
 A
0,935
3.
Для
качественного
изделия
с
третьей
линии
0,8
B
 0,171 .
P 3   0,2 
 A
0,935
имеем:
3
47
Пример 3
Бинарный источник дискретных сообщений передаёт 1 и 0 с априорными
вероятностями P1 и P0=1─P1. В канале вследствие действия помех возникают
ошибки. Условная вероятность ошибочного приёма нуля при передачи
единицы равна P(0´/1), а условная вероятность ошибочного приема единицы
при передачи нуля равна P(1´/0). Найти условную вероятность передачи
единицы P(1/1´) и нуля P(0/1´), если на приёмном конце получена единица 1´.
Найти условную вероятность передачи единицы P(1/0´) и нуля P(0/0´), если на
приёмном конце получен ноль 0´.
Исходные данные: P1=0,6; P(0´/1)=0,2; P(1´/0)=0,1.
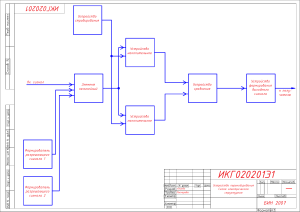
На рисунке показан процесс передачи бинарного сигнала в цифровом
канале с помехами.
P (1)
P(1)
P(1)
P(1)
P(0 1)
P(1)
P(1 0)
P(1)
P(0)
P(1)
P(1)
P(0)
Найдём полную вероятность того, что на приёмном конце получена
единица P (1) или ноль P(0) :
P(1)  P(1) P(1 / 1)  P(0) P(1 / 0) ,
P(0)  P(1) P(0 / 1)  P(0) P(0 / 0) .
По формуле Байеса для условной вероятности при приеме «единицы» и
«нуля» имеем:
P(1) P(1 / 1)
,
P(1 / 1) 
P(1)
P(0) P(0 / 0)
.
P(0 / 0) 
P(0)
Сумма условных вероятностей событий P(1 / 0) и P(0 / 0) составляет
полную группу событий, поэтому для них выполняется условие
P(1 / 0)  P(0 / 0)  1. Аналогично для условных вероятностей справедливо
P(0 / 1)  P(1 / 1)  1 .
Подставляя данные условия задачи в полученные выражения имеем:
P(1)  0,52; P(0)  0,48; P(1 / 1)  0,923; P(0 / 0)  0,75.
48
Условные вероятности при приеме нуля и единицы составляют полную
группу событий, откуда получим:
P (1 / 1)  P (0 1)  1 ,
P(0 / 0)  P(1 0)  1 .
Подставляя численные значения окончательно имеем P(0 / 1)  0,077 ,
P(1 / 0)  0,25 .
Пример 4
По каналу связи, подверженному воздействию помех, передается одна из
двух команд управления в виде кодовых комбинаций «11111» или «00000» с
априорными вероятностями появления 0,7 и 0,3 соответственно. Наличие
помех приводит к уменьшению вероятности правильного приема «0» и «1» до
величины p  0,6 при независимых ошибках передаваемых символов в
кодовой комбинации. На выходе приемного устройства зарегистрирована
комбинация «10110». Найти вероятности передачи входных команд для
принятия «оптимального» решения устройства управления.
Обозначим за А – событие, состоящее в приеме комбинации «10110».
Под гипотезой H1 будем предполагать, что была передана комбинация
«11111» с вероятностью P ( H1 )  0,7 , а гипотезой H 2 – комбинация «00000» с
вероятностью P( H 2 )  0,3 . Найдем условную вероятность приема кодовой
комбинации «10110» вместо «11111». Она равна:
P( A H1 )  p(1  p ) pp(1  p )  0,6  0,4  0,6  0,6  0,4  0,035
Аналогично условная вероятность приема кодовой комбинации «10110»
вместо «00000» равна:
P( A H 2 )  (1  p ) p(1  p )(1  p ) p  0,4  0,6  0,4  0,4  0,6  0,023
Найдем полную вероятность события А:
P( A)  P( H1 ) P( A / H1 )  P( H 2 ) P( A / H 2 )  0,0314
По формуле Байеса имеем:
P( H1 ) P( A / H1 )
 0,78 .
P( H1 / A) 
P( A)
Аналогично для условной вероятности передачи нулевой комбинации
имеем:
P( H 2 ) P( A / H 2 )
P( H 2 / A) 
 0,22 .
P( A)
Сравнивая условные вероятности передачи кодовых комбинаций
«оптимальный» приемник принимает решение: был передан управляющий
сигнал «11111».
49
Пример 5
В бинарном канале связи передается последовательность из нулей и
единиц. Вероятность ошибки при передачи бита равна P01  P10  102 .
Определить вероятность того, что при приеме байта информации произойдет
ошибка в двух битах.
Вероятность двукратной ошибки P( 2)  P012 (1  P01 )6 в конкретной
кодовой комбинации.
Вероятность двукратной ошибки с учетом случайного расположения
ошибочных
символов
в
передаваемом
сообщении
равна
8! 4
( 2)
Pош
 C82 P( 2) 
10 (0,99)6  28  0,0001 0,941  0,00263.
6!2!
Пример 6
Производится 6 независимых выстрелов по цели. Вероятность попадания
в цель при одном выстреле p  0,75 . Вычислить:
1. Вероятность пяти попаданий;
2. Вероятность не менее пяти попаданий;
3. Вероятность более трех промахов.
1. Вероятность промаха равна q  1  p  0,25. Вероятность пяти попаданий
из шести выстрелов равна P65  C65  p5  q  0,356 .
2. Вероятность того, что будет не менее пяти попаданий при стрельбе
складывается из вероятности 5 из 6 попаданий и 6 из 6 попаданий и
равна: P6n (n  5)  C65 p5q  C66 p6  0,534 .
3. При шести выстрелах будет более трех промахов эквивалентна тому, что
при шести выстрелах будет меньше трех попаданий: ни одного
попадания, или одно попадание, или два попадания. Тогда имеем:
P6n (n  3)  q6  C61  p  q5  C62  p 2  q4  0,0376 .
1.7.2. Случайные величины. Законы распределения
Пример 7
Известно, что случайная величина  представлена статистически
 x1 , x2 ,..., xn  . Она имеет
независимыми выборочными значениями
50
математическое ожидание m1  m и дисперсию M 2   2 . Найти
математическое ожидание и дисперсию случайной величины  0 , совпадающей
1 n
со средним арифметическим выборочных значений X 0   xi .
n i 1
1. Найдем математическое ожидание:
1 n  1 n
m1X 0   m1  xi    m1xi   m .
n  i 1  n i 1
2. Найдем дисперсию:
2

2
 1 n

 
1 n
2
2
.
M 2 ( X 0  m)  m1   xi  m   m1  2  xi  m  
n
n
n
1
1
i
i










Видно, что точность (СКО) измерения усредненного значения
улучшается в n раз.


Пример 8
Пусть плотность вероятности случайной величины  , принимающая
случайное значение x подчиняется нормальному (гауссовскому) закону
распределения:
 ( x  m) 2 
1
 .
W ( x) 
exp  
2
2

2


Показать, что первый и второй центральные моменты равны m1  m , а
M 2   2 .
1. Найдем МО:
 ( x  m)2 
1 
m1 
 x  exp   22 dx 
2   


.
2
2






m
( x  m)
( x  m)
1
dx
dx 
( x  m)  exp  
 exp  



2
2
2
2   


2
2







Первый интеграл равен нулю, поскольку функция под знаком интеграла
нечетная, а интеграл имеет симметричные пределы.
Второй интеграл из условия нормировки:
 ( x  m) 2 
1 
 exp   22 dx  1 .
2  


Откуда m1  m .
2. Найдем дисперсию:
51
 ( x  m) 2 
1 
2
dx
M 2  
( x  m)  exp  

2
 .

2  
2


Сделаем замену переменной t 
xm
и получим

 t2 
2   2
M 2  
 t exp   2 dt .
2  


 t2 
Проведем интегрирование по частям u  t , dv  t exp  dt
 2
 t2 
2
M 2  
t exp  
2
 2


 t2 
2  

exp  dt   2 .

2  
 2
Первое слогаемое равено нулю, а второе сводится к интегралу Пуассона

 t2 
 exp   2 dt  2 .



Пример 9
Плотность вероятности случайной величины  , принимающей
непрерывные случайные значение x , подчиняется гауссовскому закону
 ( x  m) 2 
1
 .
W ( x) 
exp  
2
2
2 

1. Найти вероятность того, что случайная величина лежит в пределах
  ,  , где    .
2. Найти вероятность попадания:
1.   ( m  ), ( m  ) ;
2.   ( m  2), ( m  2);
3.   ( m  3), ( m  3).
Найдем искомую вероятность:
 ( x  m) 2 
1 
P     
 exp   22 dx  F ()  F  ,
2  

2
z
 ( x  m) 
1
dx – функция распределения гауссовского
exp  
где F ( z ) 

2
2  
2



xm
закона. Сделаем замену переменной t 
, имеем:

52
m

 t2 
1
  m
m
P     
exp   dt   
  
,


2

2   m







 t2 
1 x
где  ( x ) 
 exp   2 dt
2  


– интеграл вероятности, для которого
справедливо (  x )  1  ( x ) .
Для вероятностей попадания в интервал (m  ), (m  2), (m  3) можно
найти с использованием таблиц интеграла Пуассона:
1. Pm      m    0,682 ;
2. Pm  2    m  2  0,954 ;
3. Pm  3    m  3  0,997 .
Пример 10
Ошибка измерения дальности  до неподвижной цели подчинена
гауссовскому закону плотности распределения с математическим ожиданием
m (регулярная ошибка) и среднеквадратическим отклонением  (случайная
ошибка). Определить вероятность того, что:
 измеренное значение дальности отклоняется от истинного значения не
более, чем на d ;
 при трех независимых измерения ошибка хотя бы одного измерения не
превзойдет по абсолютной величине d .
Данные для решения задачи: m =5м,  =10м, d =15м.
Определим вероятность того, что измеренное значение дальности
отклонится от истинного значения (начало координат) не более чем на d . Она
сводится к вычислению вероятности попадания случайной величины 
(ошибка измерения) в интервал значений – d до + d . Поскольку 
подчиняется гауссовскому закону распределения
 ( x  m) 2 
1
W ( x) 
exp 
,
2
 2
2 

то вероятность попадания случайного значения дальности  в интервал
значений (α, β), где α< β, равна
  m
m
Р (   x  )   
  
,
  
  
53
 t 2 
1 z
где  ( z ) 
 exp  2 dt – интеграл вероятности.
2  


Используя приведенные выражения и таблицы интеграла вероятности,
  15  m 
 15  m 
 . Для данных условий
  



  
можно получить вероятность P1  
задачи имеем P1  0,682 .
Вероятность того, что при трёх независимых измерениях ошибка X хотя
бы одного измерения не превзойдет по абсолютной величине d можно
определить по формуле:
P2  1  (1  P1 )3 .
Для данных условий задачи имеем:
P2  1  (1  P1 ) 3  1  (1  0,682) 3  0,9678
Пример 11
Пусть плотность вероятности случайной величины  принимающая
случайное значение x  0 подчиняется релеевскому закону:
 x2 
x
W ( x )  2 exp   2  .

 2 
Найти:
1. Условие нормировки;

;
2. Математическое ожидание m  
2


3. Дисперсию 2   2  2   ;
2

4. Медиану xm   ln 4    1,177 ;
5. Моду xmax   .
Имеем:


 x2 
 x2 
1


1. 2  x  exp  2 dx   exp   2 
 2 
 2 
 0



0

 0  1  1 – условие нормировки;


 x2 
 x2 
 x2 





2. m   x 2 exp  2 dx   x exp  2    exp  2 dx   ;
2

0
0
 2 
 2  0
 2 
x
54


 x2 
 x2 
x3
 2   x 2  2  exp  2 dx  m2   2 exp  2  


0
 2  0
 2 
3.
;
2

 x 


 2  x  exp  2 dx  m2   2  2  
2

0
 2 
x

 xm2  1
 x2 
 x2 
1 
4. 2  x  exp   2 dx   exp   2   exp   2   . Откуда можно
 xm
 2  2
 2  x
 2 
m
получить xm   ln 4    1,177 .
2
2
2

 xmax
 xmax
 xmax
dW ( x )
5.
 0 , откуда имеем exp   2   2 exp   2  и окончательно
dx
 2 
 2  
xmax   .
Пример 12
Плотность вероятности W (x) случайной величины  имеет вид
W ( x)   exp(  x ), для – ∞ < x < + ∞,
где  и  – постоянные величины.
Найти соотношение, которому должны удовлетворять постоянные  и
 , вычислить и построить функции распределения F (x) и W (x) для   2 .
Из условия нормировки имеем:

0

 1 1  2
  exp(  x )dx    exp(   x )dx   exp(   x )dx     
. Для






0
 

выполнения условия нормировки необходимо   2 . Для   2 плотность
вероятности равна W ( x)  exp( 2 x) . Для функции распределения имеем
x
для x  0
0,5 exp( 2 x),
F ( x)   exp( 2 x )dx  

1  0,5 exp( 2 x), для x  0

1.7.3. Случайные процессы
Пример 13
Найти плотность вероятности W ( x1 , x2 ) двумерного гауссовского
случайного процесса со статистическими характеристиками m1 , 1 , m2 ,  2 , и
55
вектор-столбцом выборочных значений
x 
X   1  , вектор-столбцом МО
 x2 
m 
и
матрицей
коэффициентов
взаимной
корреляции
m   1 
m
 2
 12
1 2 r 
.
R  
2 
r



 1 2
2 
Из общего выражения для двумерной плотности вероятности в
векторной форме имеем:
T

1

 X  m  R 1 X  m 
W ( x1 , x2 ) 
exp 
,
2


2 R


где R  1222 (1  r 2 ) .
Найдем обратную матрицу взаимной корреляции. Для коэффициентов
обратной матрицы имеем:
д
i  j Ri , j
1
,
Ri , j  (1)
R
где Riд, j – алгебраическое дополнение коэффициентов матрицы корреляции.
Для обратной матрицы коэффициентов корреляции имеем:
r 
 1



2


1

1 2

1
.
R 1 
2

1
r
1 r 
 

 22 
 1 2
Подставляя R 1 в векторно-матричное выражение, и производя операции,
получим:

 ( x1  m1 ) 2 2r ( x1  m1 )( x2  m2 ) ( x2  m2 ) 2  
1
1
W ( x1 , x2 ) 



exp

 .
2 
2
2
2

r




2
(
1
)
21 2 1  r


1
2
1 2

Пример 14
Совместная двумерная плотность вероятности коррелированных
случайных величин W ( x1 , x2 ) подчиняется гауссовскому распределению:
56

 ( x1  m1 ) 2 2r ( x1  m1 )( x2  m2 ) ( x2  m2 ) 2  
1
exp 
W ( x1 , x2 ) 



2 
2
2


r
2
(
1
)


 22
21 2 1  r


1 2
1

1
где m1 , m2 , 1 ,  2 , r – средние значения, СКО и коэффициент взаимной
корреляции случайных отсчетов.
Определить:
1. Одномерные плотности вероятности W ( x1 ),W ( x2 ) случайных величин;
2. Условные плотности вероятности W ( x1 / x2 ),W ( x2 / x1 ) .
Для некоррелированных случайных величин r  0 , откуда имеем:
 1  ( x1  m1 ) 2 ( x2  m2 ) 2  
1

exp  
W ( x1 , x2 )  W ( x1 )W ( x2 ) 
 
2
2
2
212


2
1




 (x  m ) 
 (x  m ) 
1
exp  1 2 1  exp  2 2 1 
212
21 
2 2 


2
2
W ( x1 , x2 )
. Подставляя
W ( x2 )
выражения и после не сложных преобразований, имеем:
По
определению
W ( x1 / x2 ) 
W ( x1 x2 ) 
.
соответствующие
2

 x 2  m2
x1  m1  
1
exp 
r
 .
2 
1  
2(1  r 2 )
 2(1  r )   2

1
1
Аналогичное выражение
вероятности W ( x2 / x1 ) .
можно
получить
для
условной
плотности
1.7.4. СП в линейных системах
Пример 15
Найти АКФ белого гауссовского шума на выходе фильтра с
1
 1(t )  1(t  и ), для 0  t  и
прямоугольной ИХ g (t )   и
.

t  и
 0,
Найдем АКФ ИХ фильтра
57

Rg ( )   g (t ) g (t  )dt 
0
можно найти для
 
1 
Rg ( )  1   .
и  и 
АКФ БГШ R (t ) 
1
и
1 
 
dt  1   для   0 . Аналогично
2 


и 
и
и
  0 . Объединяя результаты окончательно имеем:
N0
N
(t ) , где 0 – спектральная плотность мощности шума.
2
2
Найдем АКФ шума на выходе фильтра:

 
t 

N0 
N 
dt  0 1   .
(t )1 
R ( )   R (t ) Rg (   t )dt 

и 
2 и  
2 и  и 


Пример 16
Найти АКФ шума на выходе интегрирующей RC-цепочки при
воздействии на её входе БГШ. Решить во временной и частотной области.
 t 
1
Решение во временной области. ИХ фильтра g (t )  exp    , где
0
 0 
0  RC – постоянная времени цепи.
Найдем АКФ ИХ фильтра:

  2t 
 
1 
1
exp    ,
Rg ( )   g (t ) g (t  )dt  2  exp   dt 
20
0 
 0 0 
 0 

с учетом положительных и отрицательных сдвигов по  , получим:
 
1
exp    .
Rg ( ) 
2 0
 0 
Найдем АКФ шума на выходе фильтра как свертку АКФ БГШ и АКФ
 
N
фильтра и получим окончательно: R ( )  0 exp    .
4 0
 0 
Решение в частотной области. Передаточная функция фильтра есть
Фурье преобразование от ИХ. После вычислений получим:
1
K ( j) 
.
1  j0
На выходе фильтра имеем случайный процесс со СПМ:
58
G ()  K ( j)
2 N0
.
2
Фурье
Найдем АКФ выходного шума, как
преобразование от его
энергетического спектра:
1 
1 
R ( ) 
 G () exp( j)d    G ( ) cos d 
2  
0
.

 
cos 2f
N0
  
 N0 

exp
df
2 2 2

4



1
4
f
 0 
0
0
0
Из полученного выражения видно, что анализ прохождения шума на выход
фильтра во временной и частотной областях дают одинаковый результат.
Пример 17
На вход электрической цепи (см. рисунок) поступает напряжение
«белого» гауссовского шума n(t ) со спектральной плотностью мощности N 0 =
10– 18вт/гц.
Найти и построить АКФ R(τ) и мощность шума σ2 на выходе цепи по данным:
R1 =100ом, R2 =500ом, C1 =100пф.
Найдем передаточную функцию цепи. Передаточная функция цепи равна
R2

K ()  K ( j) 
, где T    R1  C1 , а  
- коэффициент
R1  R2
1  2T 2
затухания цепи.
2
N0
.
Энергетический спектр шума на выходе цепи G() 

2 1  2T 2
АКФ шума на выходе цепи найдем как обратное Фурье-преобразование
от выходного энергетического спектра:
 
N 0   2 exp( j)d N 02   cos   d N 02


R ( ) 
exp
   .


4T
4   1  2T 2
4   1  2T 2
 T
2 N 0
N 0
Дисперсия шума на выходе фильтра равна  
.

4T
4 R1C1
2
Ответ:   0,83 ; R1C1  1010 сек ;   4мв .
59
1.7.5. СП в нелинейных системах
Пример 18
Напряжение U , являющееся нормальной СВ со средним значением m и
с дисперсией  2 , подаётся на нелинейный элемент с вольтамперной
характеристикой вида:
I (U )  aU n , при U  0 ;
I (U )  0 , при U  0 ;
a  0.
Какова плотность вероятности W (I ) СВ I на выходе нелинейного
элемента?
Данные для решения задачи:  2 =1, n =1,2.
Известна плотность вероятности входного напряжения по гауссовскому
 U2 
1
закону W (U ) 
exp  2  .
 2
 2 
Для решения задачи находим функцию обратную ВАХ I = a U n , при U  0 .
dU 1
I
 для U >0.
Для n=1 имеем U  и производная
dI
a
a
Искомая плотность вероятности с учетом нормирующего множителя имеет
вид:


dU ( I ) 
1
I 2  


exp  2 2  .
W ( I )  0,5   (0)  W (U ( I ))
  0,5  (0) 


dI 


2
a

 2a   

Для n=2 имеем U  
dU
1
I

и производная
для U >0.
a
dI
2 aI
Обратная функция неодназначная, поэтому в распределениях
необходимо учитывать отдельно для положительных и отрицательных
значений обратной функции. Для n=2 при I  0 , получим:

I  
I 
1   I 
1

 W    W 
exp 
.
 
a    2aI
2 aI   a 
 2a 2 

Значение плотности вероятности для I  0 равно W ( I )  0 .
W (I ) 
60
Пример 19
Напряжение U , являющееся нормальной случайной величиной со
средним значением m =0 и с дисперсией  2 , подаётся на нелинейный элемент
с вольтамперной характеристикой вида:
1. I (U )  a U ;
2. I (U )  aU 2 .
Для постоянного a справедливо a  0 . Какова плотность вероятности W (I )
СВ I после преобразования в нелинейном элементе?
Известна плотность вероятности входного напряжения по гауссовскому
 U2 
1
exp  2  . Для решения задачи находим функцию
закону W (U ) 
 2
 2 
обратную ВАХ и модуль её производной. Имеем:
dU 1
I
 . Функция неоднозначная и имеет две ветви.
1. U  и производная
dI
a
a
dU
1
I

2. U  
и производная
так же неоднозначна.
dI
a
2 aI
Поэтому выходная плотность вероятности будет иметь так же две ветви:
1
I 
I
dU ( I )  W    W   
 a  a
1. W ( I )  W U ( I )
 a  , для I  0;
dI
0,
для I  0.
 1   I

I 
dU ( I ) 
  W  

W 

2. W ( I )  W U ( I ) 
  2 aI
a
a

, для I  0.

 
dI

0,
для I  0.

Функция W () – гауссовский закон распределения от своего аргумента.
Пример 20
Найти функцию распределения и плотность вероятности двух
независимых случайных величин, 1 ,2 – отклонения от центра мишени  в
двух
взаимно
перпендикулярных
направлениях.
Полагаем
m1  m2  0, 1  2   .
Значения величин , 1 , 2 обозначим соответственно y , x1 , x2 .
61
Функция распределения F ( y ) величины y равна вероятности того, что
конец вектора с проекциями x1 и x2 не выйдет за пределы окружности радиуса
y  x12  x22 или
F ( y ) 
 W ( x1, x2 )dx1dx2 ,
( 2)
x12  x 22  y
где двумерная плотность вероятности имеет вид
W( 2 ) ( x1, x2 ) 
 x12  x22 
1
.
exp  
2 
22
2



Перейдем к полярным координатам (, ) заменой переменных:
x1   cos 
x2   sin 
.
Тогда имеем:
 2  ( x1, x2 )
1 2 y
F ( y ) 
  exp   22  (, ) dd,
22 0 0


где якобиан преобразования равен:
x1
( x1 , x2 )


x2
(, )

x1
 cos    sin 

 .
x2 sin   cos 

После вычислений функции распределения имеем:
62
y
1 2 y
 2 
 2 
F ( y ) 
 d  exp   2 2 d   0 d exp   2 2  
22 0 0




 y2 
 1  exp   2 , y  0.
 2 
Вычислим плотность распределения Релея. Она имеет вид:
dFy ( y ) y
 y2 
W ( y ) 
 2 exp   2 , y  0 .
dy

 2 
Пример 21
Пусть ( 1 , 2 ) – случайные декартовые координаты некоторой точки
( x1 , x2 ) (конца вектора) на плоскости. Задана плотность вероятности
W( 2) ( x1, x2 ) . Пусть входные процессы ( 1 , 2 ) статистически независимы,
имеют гауссовское распределение с параметрами m1  a, m2  b; 1  2   .
Найти
совместную плотность вероятности W( 2) ( y1, y2 ) значений
случайных величин ( 1 , 2 ) вида
1  12  22 ,
1  0;
.
2  arctg 2 1, 0  2  2
Обозначим значения величин ( 1 , 2 ) соответственно (, ) , вместо (
y1 , y2 ), как это обычно принято при переходе к полярным координатам.
Декартовы координаты связаны с полярными следующими нелинейными
соотношениями:
x1    cos 
.
x2    sin 
Якобиан преобразования имеет вид:
( x1, x2 ) cos    sin 

 .
sin   cos 
(, )
Тогда
и
для
W( 2) (, )    W( 2) ( cos,  sin )
независимых входных процессов имеем:
W( 2) (, )    W1 ( cos )  W2 ( sin ) .
Заметим, что величины (, )
статистически независимыми.
63
статистически
в последнем случае не являются
Для одномерных распределений модуля  и фазы  вектора ( x1 , x2 ) в
общем случае имеем:
2
W1 ()    W( 2 ) ( cos ,  sin )d – для начальной фазы;
0

W2 ()   W( 2 ) ( cos ,  sin )d – для огибающей процесса.
0
Для двумерной плотности распределения имеем:
 ( x1  a )2  ( x2  b)2 
1
( 2)
W ( x1, x2 ) 
exp 
.
2
22
2



Перейдем к полярной системе координат и получим:
 ( cos   a )2  ( sin   b)2 

( 2)
W (, ) 
exp 
.
2

2
22


Одномерная плотность распределения огибающей  выходного процесса
равно:
 2
 1
2
2 
W () 
exp
 2 ( cos   a )  ( sin   b) d 
2 
2 0
 2

.
 2  a 2  b2  2 




exp  

  exp  2 ( a cos   b sin )d
2
2
2
2



0
Обозначим Z  a 2  b2 ;   arctg b , тогда имеем:
a

  2  Z 2   Z 
W ()  2 exp 
2
  I 0   2  ,
2




2
1
где I 0 ( x ) 
 expx  cos(  )d − модифицированная функция Бесселя
2 0
нулевого порядка. Распределение называется распределением Релея-Райса,
или обобщенным релеевским.


64
2. ОСНОВЫ СТАТИСТИЧЕСКОЙ ТЕОРИИ
ОБНАРУЖЕНИЯ СИГНАЛОВ
2.1. Задачи статистической теории обработки сигналов
Пусть есть радиотехническая система (РТС), под которой будем
понимать совокупность устройств передачи, либо извлечения информации,
выполняющих единую целевую задачу. Под такой системой будем понимать в
первом случае радиотехническую систему передачи информации (РСПИ), а во
втором совмещенную обзорную радиолокационную систему (РЛС).
При передаче полезного сигнала в канале передачи информации на вход
радиоприемного устройства совместно с сигналом поступают различного рода
помехи и шумы. Примером таких помех в РСПИ могут служить частотновременные искажения сигнала при распространении
в радиоканале и
собственные тепловые шумы на входе приемного устройства, а для РЛС
искусственные и естественные помехи и тепловые шумы.
Искажения полезного сигнала от помех носят случайный характер,
поэтому не могут быть устранены регулярными методами. Наличие помех
приводит к искажению полезного сигнала и снижает качество принимаемой
информации.
Будем
называть
радиоприемное
устройств
(РПУ),
обеспечивающее минимальный уровень искажения полезного сигнала при
фиксированном уровне помех, оптимальным или идеальным при выбранном
критерии оптимальности.
Критерии оптимальности и количественные характеристики искажений
зависят от типа и назначения приемного устройства. Минимальный уровень
искажений при выбранном критерии качества работы оптимального РПУ
характеризует потенциальную помехоустойчивость. Любой другой приемник
может обеспечить помехоустойчивость строго меньше потенциальной.
Синтез оптимальных устройств обработки по заданному критерию с
известными статистическими характеристиками сигналов и помех является
одной из основных задач теории оптимального обнаружения и различения
сигналов.
Другой важной задачей статистической теории является анализ влияния
работы отдельных устройств на качественные показатели приемного
устройства в целом по заданному критерию.
В зависимости от целевого назначения РТС решают разные задачи
получения полезной информации, поэтому к ним предъявляются различные
требования и критерии оценки качества их работы. Исходя из них, можно
сформулировать ряд задач обработки сигналов на фоне помех:

обнаружение сигнала;
65

различение сигналов;

разрешение по параметру сигнала;

оценка параметра сигнала;

фильтрация параметра сигнала.
Сформулируем кратко эти задачи.
1. Обнаружение сигналов.
Пусть на вход РПУ на интервале наблюдения t  [0, T ] действует аддитивная
смесь сигнала s(t ,  ) и помехи n(t ) , где  (1,  2 ,...,  m ) - вектор
информационных и случайных параметров сигнала:
u(t )  s(t,  )  n(t ) ,
где  – случайный параметр, принимающий значения   0,1; 0 – при
отсутствии сигнала и 1 – при его наличии. Пусть известны статистические
характеристики случайных параметров сигнала и шума.
Оптимальный приемник должен вынести оценку случайного параметра
̂ и принять гипотезу о наличие сигнала на входе приемника H1, ˆ  1 или
гипотезу H 0 , ˆ  0 о его отсутствии.
2. Различение сигналов.
Пусть на вход РПУ на интервале наблюдения t  [0, T ] действует аддитивная
смесь набора сигналов вида si (t,  ) , где i  1, N  и шума n(t ) :
u(t )  si (t,  )  n(t ) .
Под набором сигналов si (t,  ) , имеющих вектор параметров  (1,  2 ,...,  m )
можно подразумевать некий алфавит символов, имеющих априорную
(доопытную) вероятность появления на входе РПУ pi . Пусть известны
статистические характеристики случайных параметров сигнала и шума.
Необходимо по принятой реализации принять решение о наличии
конкретного сигнала (символа алфавита) sk (t ,  ) на входе приемника.
3. Разрешение сигналов.
Пусть на вход РПУ на интервале наблюдения t  [0, T ] действует аддитивная
смесь двух сигналов вида s(t ,  ) , где вектор параметров  (1,..., ,..., m )
содержит информационный параметр  и шума n(t ) :
u(t )  s1(t , 1,..., 1,...,  m )  s2 (t , 1,..., 2 ,...,  m )  n(t ) .
Пусть известны статистические характеристики случайных параметров
сигнала и шума. По информационному параметру  необходимо произвести
разрешение двух близко расположенных сигналов.
Задача состоит в синтезе оптимального алгоритма различения сигналов и
оценке потенциальной (минимально возможной) разрешающей способности
приемного устройства.
66
4. Оценка параметров сигнала.
Пусть на вход РПУ на интервале наблюдения t  [0, T ] действует аддитивная
смесь сигнала s(t ,  ) и помехи n(t ) , где  (1,..., ,..., m ) - вектор
информационных и случайных параметров сигнала:
u(t )  s (t ,  )  n(t ) .
Пусть известны статистические характеристики случайных параметров
сигнала и шума. Параметр сигнала  является информационным и подлежит
определению (измерению). Наличие помех приводит к тому, что параметр 
является случайной величиной, имеющей конечную точность определения.
Поэтому в результате измерения можно получить оценку измеряемого
параметра ̂ .
Задача состоит в синтезе оптимального алгоритма измерения
информационного параметра  .
5. Фильтрация параметра сигнала.
Пусть на вход РПУ на интервале наблюдения t  [0, T ] действует аддитивная
смесь сигнала s(t ,  ) и помехи n(t ) , где  (1,..., (t ),..., m ) - вектор
информационных и случайных параметров сигнала:
u(t )  s (t ,  )  n(t ) .
Пусть известны статистические характеристики случайных параметров
сигнала и шума. Параметр сигнала  (t ) является информационным, медленно
изменяющимся во времени, подлежит слежению во времени изменения его
величины. Наличие помех приводит к тому, что закон изменения  (t )
является случайной временной функцией, имеющей конечную точность её
изменения. В результате слежения можно получить оценку закона изменения
параметра ˆ (t ) .
Задача состоит в синтезе оптимального алгоритма оценки закона
изменения информационного параметра  (t ) .
Рассмотренные статистические задачи являются взаимосвязанными. Так
задачу обнаружения сигналов можно рассматривать как частный случай
задачи различения двух сигналов, один из которых равен нулю. Задача оценки
параметра сигнала является частным случаем задачи фильтрации, когда
параметр сигнала является постоянной величиной.
2.2. Обнаружение сигналов
Пусть имеется радиоприемное устройство, на входе которого
наблюдается входной сигнал u(t ) , представленный своими выборочными
67
значениями во временной области с интервалом t вида u (u1, u2 ,....., un ) .
Представленный сигнал состоит из детерминированного сигнала и шума:
u(t )  s(t )  n(t ) ,
где s(t ) – детерминированный (полностью известный) сигнал;
n(t ) – шум;
 – параметр, принимающий значение равное единицы в случае наличия
сигнала в принимаемой смеси и нулю в случае его отсутствия.
Необходимо синтезировать оптимальный обнаружитель сигнала, на
выходе которого необходимо принять гипотезу H1 о наличии сигнала в
принимаемой смеси, или его отсутствии H 0 . На выходе обнаружителя,
соответственно, выносится решение вида
 1, в случае гипотезы H1 ,
ˆ  
(2.1)
0, в случае гипотезы H 0
где ̂ является оценкой параметра  . Поскольку параметр  может принимать
только два значения ноль или единицу, то такой обнаружитель называется
двухальтернативным, а принимаемые при этом гипотезы H1 и H 0 - простыми.
Решение задачи заключается в отыскании правила, согласно которому по
выборочным значениям u (u1, u2 ,....., un ) и принятому критерию обнаружения
выносится оптимальное решение (2.1) о наличии или отсутствии сигнала на
входе обнаружителя.
Для решения разобьем все пространство U выборочных значений
входного сигнала вида u (u1, u2 ,....., un ) на две непересекающиеся области U1 –
присутствия сигнала на входе приемника и U 0 его отсутствия рис.2.1.
Рис. 2.1
Наличие случайного процесса n(t ) , представленного своими
выборочными значениями n( n1 , n2 ,..., nk ) , приводит к тому, что в результате
работы обнаружителя сигнала на его выходе возможны четыре варианта
решения статистической задачи:
1.
Сигнал отсутствует на входе обнаружителя, в результате его работы
принимается гипотеза H 0 , на выходе обнаружитель дает оценку случайного
параметра ˆ  0 . Совместную вероятность такого события обозначим
68
pн  p( s0 , H 0 ) – вероятность правильного необнаружения сигнала. Полагая
известной условную плотность вероятности совместного распределения
выборочных значений входного процесса u (u1, u2 ,....., un ) в виде
W (u1, u2 ,..., un / H 0 )  W (u / H 0 ) можно найти вероятность такого события:
pн   W (u / H 0 )du .
U0
2.
Сигнал присутствует на входе обнаружителя, в результате его
работы принимается гипотеза H1 , на выходе обнаружитель дает оценку
случайного параметра ˆ  1 . Совместную вероятность такого события
обозначим D  p( s1 , H1 ) – вероятность правильного обнаружения сигнала.
Полагая известной условную плотность вероятности совместного
распределения выборочных значений входного процесса u (u1, u2 ,....., un ) в
виде W (u1 , u2 ,..., un / H1 )  W (u / H1 ) , можно найти вероятность такого события:
D   W (u / H1 )du .
U1
3.
Сигнал отсутствует на входе обнаружителя, в результате его работы
принимается гипотеза H1 , на выходе обнаружитель дает оценку случайного
параметра ˆ  1 . Совместную вероятность такого события обозначим
F  p( s0 , H1 ) – вероятность ложной тревоги. Полагая известной условную
плотность вероятности совместного распределения выборочных значений
входного процесса u (u1, u2 ,....., un ) в виде W (u1 , u2 ,..., un / H 0 )  W (u / H 0 )
можно найти вероятность такого события:
F   W (u / H 0 )du .
U1
4.
Сигнал присутствует на входе обнаружителя, в результате его
работы принимается гипотеза H 0 , на выходе обнаружитель дает оценку
случайного параметра ˆ  0 . Совместную вероятность такого события
обозначим pпр  p( s1 , H 0 ) – вероятность пропуска сигнала. Полагая
известной условную плотность вероятности совместного распределения
выборочных значений входного процесса u (u1, u2 ,....., un ) в виде
W (u1 , u2 ,..., un / H1 )  W (u / H1 ) можно найти вероятность такого события:
pпр   W (u / H1 )du  1  D ,
U0
поскольку условные вероятности пропуска сигнала и его правильного
обнаружения составляют полную группу событий.
Найдем наилучшее правило принятия решения о наличии или отсутствии
сигнала на входе обнаружителя. Обозначим постоянные коэффициенты
69
«платы» за ошибки ложной тревоги и пропуска сигнала, как ошибки первого и
второго рода П 01 и П10 соответственно.
Оптимальный приемник, очевидно, должен минимизировать как ошибку
первого F и второго pпр рода, так и соответствующие платы за них. Однако,
требования одновременного снижения вероятностей F и pпр невозможно,
поскольку эти требования противоречивы. Действительно, снижение
вероятности пропуска сигнала pпр  0 до нулевых значений приводит к росту
вероятности ложной тревоги до величины F  1 и наоборот. Отсюда следует,
что в качестве критерия обнаружения сигнала необходимо выработать
компромиссный вариант минимизации ошибок первого и второго рода.
В качестве наиболее общего критерия минимизации ошибок
обнаружения и платы за них применяют байесовский критерий минимума
среднего риска:
R  П 01 p( s0 , H1 )  П10 p( s1 , H 0 )min ,
(2.2)
где П 01, П10 – платы за ошибки первого и второго рода;
p( s0 , H1 )  p( s0 ) p( H1 / s0 )  (1  p ) F – совместная вероятность отсутствия
сигнала на входе приемника и принятия гипотезы H1 в соответствии с
формулой Байеса;
p( s1 , H 0 )  p( s1 ) p( H 0 / s1 )  ppпр  p(1  D ) – совместная вероятность наличия
сигнала на входе приемника и принятия гипотезы H 0 в соответствии с
формулой Байеса;
p – априорная вероятность присутствия сигнала на входе премного
устройства.
Подставим в выражение (2.2) выражения для совместных вероятностей
ошибок первого и второго рода:
R  П10 ppпр  П 01 (1  p ) F min  П10 ppпр  l0 F min ,
(2.3)
П 01 1  p
– постоянная величина, имеющая смысл порога
П10 p
обнаружения. Выражение (2.3) называется байесовским критерием или
критерием минимума среднего риска. Эквивалентный критерий можно
получить с учетом того, что pпр  1  D , который называется критерием
максимума весовой разности:
D  l0 F max .
(2.4)
Подставим в (2.4) интегральные выражения вероятностей правильного
обнаружения и ложной тревоги:
где
l0 
70


W
u
H
d
u
l
W
u
H
d
u
(
/
)
(
/
)

.
(2.5)


1
0 
0

U1
U1
 max
Объединяя выражения под интегралами и выполняя операцию максимизации
подинтегральной разности, имеем:
 W (u / H1 )

(2.6)

l

 W (u / H ) 0  W (u / H 0 )du .


0
U
max
Выражение
1
W ( u / H1 )
 l (u ) ,
(2.7)
W (u / H 0 )
называется отношением правдоподобия.
Из выражения (2.6) следует алгоритм работы оптимального
обнаружителя по критерию максимума весовой разности или эквивалентного
ему байесовского критерия минимума среднего риска. В соответствии с
выражением (2.6) оптимальный обнаружитель детерминированного сигнала на
фоне помехи должен вычислить отношение правдоподобия и сравнить его с
порогом обнаружения. Если l (u )  l0 , то принимается решение о наличие
сигнала в принимаемой смеси, если l (u )  l0 о его отсутствии. Математически
данное утверждение можно представить в следующем виде:
H1
W (u / H1 )  1  p П 01
,
(2.8)
W (u / H 0 )  p П10
H0
1  p П 01
– порог обнаружения байесовского критерия.
где l0 
p П10
Выражение (2.8) показывает, насколько более вероятна гипотеза H1
наличия сигнала в принимаемой входной смеси, по сравнению с гипотезой H 0
его отсутствия.
Рассмотрим частные случаи:
1. Пусть плата за пропуск сигнала и ложную тревогу одинаковы
П 01  П10 . Такая ситуация может возникнуть в цифровых система передачи
данных, когда вместо нуля принимается единица и наоборот. В случаях
одинаковых плат за ошибки первого и второго рода выражение (2.8)
принимает вид:
71
H1
W ( u / H1 )  1  p
.
(2.9)
W (u / H 0 )  p
H0
Такой критерий обнаружения сигналов называется критерием идеального
наблюдателя. Порог обнаружения по критерию идеального наблюдателя
имеет вид:
1 p
,
p
где p – априорная вероятность наличия сигнала на входе обнаружителя
сигнала.
2. Пусть априорная вероятность появления сигнала на входе
обнаружителя неизвестна, либо она одинакова для наличия и отсутствия
p  0,5 . Тогда отношение
сигнала на входе приемника, т.е. равна
правдоподобия подлежит сравнению с порогом обнаружения равным единице.
Выражение (8.8) в этом случае принимает следующий вид
H1
W ( u / H1 ) 
1,
(2.10)
W (u / H 0 ) 
H0
где порог обнаружения l0  1 . Соответствующий критерий обнаружения
называется критерием максимального правдоподобия.
3. В радиолокационных системах обнаружения наибольшее
распространение получил критерий Неймана-Пирсона. В соответствии с этим
критерием выбирается минимальная вероятность ложной тревоги
F0  10 6  108 . Соответствующий порог обнаружения l0 рассчитывается
исходя из заданного значения F0 . Отношение правдоподобия в соответствии с
l0 
критерием Неймана-Пирсона сравнивается с рассчитанным порогом l0 в
обнаружителе сигнала
H1
W ( u / H1 )  
l0 .
(2.11)
W (u / H 0 ) 
H0
72
Из представленного анализа следует, что независимо от используемого
критерия обнаружения оптимальный обнаружитель детерминированного
сигнала вычисляет отношение правдоподобия (2.7) и сравнивает его с порогом
обнаружения l0 рассчитанным в соответствии с применяемым критерием. В
случае превышения порога, принимается решение о присутствии сигнала в
принимаемой смеси, в противном случае принимается решение о его
отсутствии. На рис.2.2 представлена структурная схема обнаружителя сигнала.
Рис. 2.2
Приведенный анализ позволяет сделать вывод, что оптимальный
алгоритм обнаружения детерминированного сигнала на фоне шума не зависит
от порога обнаружения l0 . Величина порога влияет на выбор критерия
обнаружения и вероятность ложной тревоги F .
С порогом обнаружения можно сравнивать как отношение
правдоподобия (2.7), так и любую монотонную функцию, например,
логарифмическую ln l (u ) . Как будет показано далее, это упрощает структуру
обнаружителя на фоне гаусовского шума.
2.3. Алгоритм оптимального обнаружения детерминированного
сигнала. Структура оптимального обнаружителя
Во многих системах связи и радиолокации возникает задача приема


детерминированных (т.е. точно известных) сигналов s(t , λ ) , где λ(λ1, λ 2 ,..., λ n )
- вектор известных параметров сигнала на фоне шума n(t ) . При этом
возникает задача установления того, присутствует сигнал на входе приемника
или отсутствует. Поскольку это обнаружение производится на фоне
случайного шума n(t ) , то задача обнаружения является статистической.
Принимаемое колебание на входе приемного устройства на интервале
наблюдения t 0,T  можно представить в виде суммы:

u(t )  θ  s(t , λ )  n(t ) ,
где θ – параметр обнаружения сигналов, равный 1 при наличии сигнала и 0 при
его отсутствии. По принятой реализации входного колебания u(t) на интервале
73
наблюдения необходимо выяснить, есть сигнал в принимаемой смеси или нет,
т.е. произвести оценку параметра:
 1, сигнал присутству ет на входе приемного уустройст а, гипотеза H1
.
θ
H
0
,
сигнал
отсутствуе
т
на
входе
приемного
уустройст
а,
гипотеза

0
В качестве критерия оптимальности будем использовать критерий
минимума среднего риска (критерий Байеса), который заключается в
минимизации вероятности суммарной ошибки:

R  П01 p( s0 , H1 )  П10 p( s1, H 0 )min ,
где p( s0 , H1 )  p( s0 ) p H1  – совместная вероятность отсутствия сигнала,
 s0 
когда при этом принимается гипотеза о его наличии H1 (ошибка первого рода);
H
p( s1, H 0 )  p( s1 ) p 0  – совместная вероятность присутствия сигнала,
s1 

когда решающее устройство принимает решение об его отсутствии (ошибка
второго рода);
П 01 и П10 – платы за ошибки первого и второго рода;
p( s1 )  p – априорная вероятность присутствия сигнала на входе приемного
устройства;
p ( s0 )  (1  p ) – априорная вероятность отсутствия сигнала на входе
приемного устройства.
Условная вероятность D  1  p H 0  - называется вероятностью
s1 

правильного обнаружения, а F  p H1  - вероятностью ложной тревоги.
 s0 
Ранее было показано, что оптимальный алгоритм обнаружения

сигналов заключается в вычислении отношения правдоподобия l (u ) и
(1  p ) П 01
сравнении его с порогом l0 
с целью принятия решения о наличии
pП10

или отсутствии сигнала s(t , λ ) в принимаемом колебании u(t). Алгоритм
работы обнаружителя соответствует правилу

 W ( u / H1 )
 l0 , наличие сигнала
  W (u / H 0 )
l(u )   
,
W ( u / H1 )
 
 l , отсутствие сигнала
W (u / H 0 ) 0
74
(2.12)

где W u H1  − условная плотность вероятности распределения выборочных
значений u (u1, u2 ,....., un ) на интервале наблюдения, взятых с интервалом

квантования t  ti  ti 1 при наличии в ней сигнала s(t , λ ) ;

W u H 0  − условная плотность вероятности распределения выборочных

значений принимаемой реализации при отсутствии в ней сигнала s(t , λ ) .
Входной шум n(t) полагаем «белым» гауссовским со спектральной
плотностью мощности равной G(f) = N0 при 0 ≤ f < . Функционал плотности
вероятности распределения отрезка гауссовского «белого» шума n(t) на
временном интервале t [0,T ] имеет вид:
 1 T 2

W nt   k exp 
n
(
t
)
dt
,

N
0 0


(2.13)
где k – нормирующий множитель. Подставим выражение (2.13) в отношение
правдоподобия (2.12) и получим алгоритм работы оптимального обнаружителя
сигналов:
 1 T
2 




,
λ
k exp 
u
t
s
t
dt 


N
00


l u(t )  
 1 T
2 




k exp 
u
t
dt 

N
00





 2 T
1 T 2


 exp 
 u t s(t , λ )dt  N  s (t , λ )dt  
N
00

 00

E 
 exp  Z 
,
N

0
2 T
Z
 ut s(t, λ )dt – значение функции взаимной корреляции между
N0 0
где
принимаемым колебанием и ожидаемым детерминированным сигналом
(корреляционный интеграл);
T
E   s 2 t , λ dt – энергия сигнала.
0
Учтем, что exp(Z) функция монотонная, поэтому с порогом в (2.12)
удобно сравнивать натуральный логарифм отношения правдоподобия. Найдем
75
логарифм отношения правдоподобия и получим следующее выражение для
алгоритма оптимального обнаружения детерминированного сигнала:
H1

2
E
u(t ) s(t , λ )dt  ln l0 
,
(2.14)

N0 0
N0
H0
(1  p ) П 01
E
где l0 
, а Z 0  ln l0 
– порог обнаружения сигнала.
N0
pП10
Из этого алгоритма следует, что оптимальный обнаружитель
детерминированного сигнала должен вычислять значение функции взаимной
корреляции Z и сравнивать его с порогом Z0. Следовательно, структурная

схема оптимального обнаружителя детерминированного сигнала s(t , λ )
состоит из последовательного соединения взаимно корреляционного (ВКУ) и
порогового устройства (ПУ). Взаимно корреляционное устройство состоит из
умножителя, на входы которого поступают соответственно принимаемое

колебание u(t) и обнаруживаемый сигнал s(t , λ ) и интегратора на время
наблюдения t  0, T . В пороговом устройстве осуществляется сравнение
выходного значения интегратора Z с порогом Z0 (рис. 2.3).
T
Рис. 2.3
Таким образом, алгоритм работы оптимального обнаружителя
детерминированного сигнала на фоне белого гауссовского шума заключается в

умножении входной смеси
u(t) на обнаруживаемый сигнал s(t , λ ) ,
интегрировании этого сигнала на интервале наблюдения и подачи результата
на вход порогового устройства. На выходе порогового устройства
вырабатывается решение (гипотеза H1) о наличии сигнала s(t) при Z ≥ Z0 , или
о его отсутствии (гипотеза H0) при Z < Z0 в принимаемой смеси u(t).
76
2.4 Характеристики обнаружения детерминированного сигнала
Определим показатели качества работы оптимального обнаружителя
детерминированного сигнала, поступающего на вход приемного устройства в
аддитивной смеси с белым гауссовским шумом. Найдем характеристики
обнаружения сигнала и определим основные показатели качества его работы.
Под характеристикой обнаружения будем понимать зависимость вероятности
правильного обнаружения D(q) при фиксированной вероятности ложной
2E
тревоги F в зависимости от отношения сигнал/шум q 
. Для отыскания
N0
характеристик обнаружения найдем условные плотности вероятности
распределения W Z H1  и W Z H 0  и соответствующие значения
вероятностей D(q) и F для случайной величины Z на входе порогового
устройства обнаружителя.
В соответствии со схемой обработки рис. 2.3 до порогового устройства
входное колебание u(t) подвергается линейному преобразованию. Поскольку
выборочные значения входного сигнала распределены по гауссовскому закону
распределения, то и на входе порогового устройства выборочные значения Z
также будут иметь гауссовское распределение. Найдем математическое
ожидание и дисперсию случайной величины Z, имеющей гауссовскую
условную плотность вероятности распределения W Z H1  и W Z H 0  .
Для случая отсутствия сигнала в принимаемой смеси имеем

2E
1

 Z2 
2
m0  0, σ 0 
, и W (Z / H0 ) 
exp  2  .
N0

2 σ 02

 2σ 0 
Для случая присутствия сигнала во входной смеси можно найти

2E
2E
1

 ( Z  q2 )2 
2
2
2
m1  q 
, σ1  σ 0 
, и W ( Z / H1 ) 
exp 
.
2
2
N0
N0

2σ 0 
2σ


0
Найдем вероятность ложной тревоги:

 Z 2 
F (Z0 ) 
dZ 1   Z н  ,
 exp 
2
2


2 σ 0 Z 0
 2σ 0 
1
(2.15)
Z
где
1 н  x2
 Z н  
e dx

2  
–
интеграл
вероятности.
В
табл.
2.1
Z
представлены значения нормированных порогов обнаружения Z н  0 для
0
77
заданных значений F вероятностей ложной тревоги, рассчитанных с
использованием выражения (2.15) и таблиц интеграла вероятности.
F
ZН
-1
-2
-3
-4
-5
-6


-7
-8
Таблица 2.1
10
10
10
10
10
10
10
10
10-9
1,282 2,321 3,090 3,719 4,265 4,753 5,199 5,612 5,998
Аналогично можно найти вероятность правильного обнаружения:
2

 Z  q2 
D( q) 
exp 
dZ 1   Z н  q ,
2 
2 
2σ0 
2σ0 Z 0


1

(2.16)
2E
– отношение сигнал/шум на входе приемного устройства. По
N0
формуле (2.16) можно рассчитать зависимости вероятности правильного
обнаружения D детерминированного сигнала в зависимости от отношения
сигнал/шум q на входе приемного устройства при фиксированных значениях
вероятности ложной тревоги F  const (см. табл. 2.1), которые называются
семейством характеристик обнаружения.
где q 
Рис. 2.4.
На рис. 2.4 представлены характеристики обнаружения, рассчитанные по
формуле (2.16). Из них следует, что для повышения вероятности правильного
обнаружения D сигнала необходимо увеличивать отношение сигнал/шум q на
входе порогового устройства по сравнению с относительным порогом ZН.
Значение порога, в соответствии с критерием обнаружения Неймана-Пирсона,
78
выбирается в соответствии с (2.15) для требуемой величины вероятности
ложной тревоги F. Тогда повышение вероятности правильного обнаружения D
можно добиться только путем увеличения энергии сигнала E.
Пороговым отношением сигнал/шум называется минимальное
отношение qпор , при котором сигнал обнаруживается с заданной
вероятностью D* при фиксированной вероятности F*. Его значение может
быть найдено из характеристик обнаружения на рис. 2.4. Сигналы, имеющие
q  qпор для заданного значения F*, будут иметь D  D .
2.5. Алгоритм оптимального обнаружения сигнала со случайной
начальной фазой. Структура оптимального обнаружителя
Пусть на входе приемного устройства, на временном интервале t  0, T 
наблюдается колебание вида:
u(t )  θ  s(t )  n(t )  θ  S cos(ω0t  )  n(t ) ,
где θ – параметр обнаружения сигналов, равный 1 при наличии сигнала и 0 при
его отсутствии;
S и ω 0 – детерминированные параметры амплитуды и частоты сигнала;
 – случайная начальная фаза, равномерно распределенная на интервале
1
  0,2 π , с плотностью вероятности распределения W () 
.
2π
По принятой реализации входного колебания u(t) на интервале наблюдения
t  0, T  необходимо выяснить, есть сигнал в принимаемой смеси, или нет.
Совместно с сигналом действует «белый» гауссовский шум n(t ) спектральной
плотности мощности N0. В результате решения задачи необходимо получить
алгоритм работы оптимального обнаружителя сигнала со случайной начальной
фазой.
Известно, что в результате оптимальной обработки необходимо
вычислить отношение правдоподобия и сравнить его с порогом обнаружения:
 W (u / H1, )
 l0 , наличие сигнала

 W (u / H 0 )
.
(2.17)
l(u, )  
W (u / H1, )

 l0 , отсутствие сигнала

 W (u / H 0 )
Отношение правдоподобия (2.17) является условным, поскольку зависит от
случайного параметра  . Для получения безусловного отношения
правдоподобия произведем его усреднение по случайному параметру:
79
2π
W (u / H1, )
d .
(2.18)
W
u
H
(
/
)
0
0
После подстановки в (2.18) выражения (2.13) и проведения интегрирования
получим
2π

 E
W (u / H1, )
S T 2π
(
)
cos(
ω
)
l (u )  
d  exp 
u
t
t
dtd




 . (2.19)

0
(
/
)
π
W
u
H
N
N
0
0
00 0


0
l (u )  
Безусловное отношение правдоподобия, после усреднения по случайному
параметру  и интегрирования по времени, имеет вид:
 E   2Z 
 I 0 
 ,
(2.20)
l (u )  exp  
N
N
0  0

где Z  Z12  Z 22 – корреляционный интеграл;
T
Z1  S  u(t ) cos ω0tdt – синфазная составляющая корреляционного интеграла;
0
T
Z 2  S  u(t ) sin ω0tdt – квадратурная составляющая корреляционного
0
интеграла;
Z1
Z
 cos, а 2  sin  – нормированные синфазная и квадратурные
Z
Z
составляющие корреляционного интеграла;
 2Z

 2Z  1 2π
 
I 0 
exp
cos(


φ
)

d – модифицированная функция Бесселя

N
2
π
N
 0

 0
0
нулевого порядка;
S2
E   s t dt 
τ c – энергия сигнала;
2
0
T
2
τ c – длительность радиоимпульса.
Алгоритм работы оптимального обнаружителя сигнала со случайной
начальной фазой заключается в сравнении отношения правдоподобия (2.20) с
порогом, согласно выражению (2.17). Учитывая, что модифицированная
функция Бесселя является монотонно возрастающей функцией своего
аргумента, с порогом обнаружения можно сравнивать корреляционный
интеграл:
80
H1
Z  Z12  Z 22

Z0 ,

(2.21)
H0
где Z 0 – порог обнаружения. Алгоритм работы обнаружителя (2.21) сводится к
вычислению двух квадратурных составляющий, их суммированию и
вычислению квадратного корня.
Рис. 2.5
На рис. 2.5 показана структурная схема оптимального обнаружителя
сигналов со случайной начальной фазой. Она представляет собой схему с
двумя квадратурными каналами, в каждом из которых осуществляются
операции умножения, интегрирования и возведения в квадрат. Опорные
напряжения в каналах сдвинуты по фазе друг относительно друга на π .
2
Наличие двух квадратурных каналов позволяет получить результат обработки
Z, не зависящий от начальной фазы входного колебания.
2.6. Характеристики обнаружения сигнала
со случайной начальной фазой
Определим показатели качества обнаружения сигнала со случайной
начальной фазой. Для этого необходимо вычислить плотности вероятности
распределения огибающей сигналов Z при наличии и отсутствии во входной
смеси случайного сигнала. Известно, что огибающая гауссовского шума будет
распределена по закону Релея, а смесь сигнала и шума – по закону РелеяРайса:
 Z2 
Z
W Z H 0   2 exp   2 
 2σ 
σ


,
(2.22)
2
2

Z
Z  E   ZE 
W Z H1   2 exp  
I
2  0 2 

σ
2σ

 σ 
81
EN 0
– дисперсия шума на входе порогового устройства. Для
2
Z
нормированного значения корреляционного интеграла Z н  0 можно найти

вероятности ложной тревоги и правильного обнаружения сигнала:

 Z2 
 Z н2 



F   Z exp 
dZ  exp  
 2 
 2 
Zн




,
(2.23)

 Z 2  q2 
 I 0 Zq dZ
D   Z exp  


2
Zн


где σ 2 
2E
– отношение сигнал/шум.
N0
В табл. 2.2 представлены значения нормированных порогов обнаружения
Z
Z Н  0 для заданных значений F вероятностей ложной тревоги,
σ
рассчитанные с использованием выражения (2.23).
где q 
-2
-3
-4
-5
-6
-7
-8
Таблица 2.2
10
10
10
10
10
10
10
10
10-9
2,146 3,0349 3,7169 4,2919 4,7945 5,2565 5,6777 6,0697 6,4379
Характеристики обнаружения сигнала со случайной начальной фазой
имеют тот же вид, что и при известной начальной фазе, но лежат несколько
правее. Это свидетельствует о том, что при заданной вероятности ложной
тревоги и правильного обнаружения в обнаружителе сигнала со случайной
начальной фазой имеется проигрыш в отношении сигнал/шум по сравнению с
обнаружителем детерминированного сигнала.
F
ZН
-1
2.7. Алгоритм оптимального обнаружения сигнала со случайной
амплитудой и начальной фазой. Структура оптимального обнаружителя
Пусть на входе приемного устройства, на временном интервале t  0, T 
наблюдается колебание вида:
u(t )  θs(t , a, )  n(t )  θas(t ) cos(ω0t  )  n(t ) ,
где θ – параметр обнаружения сигналов, равный 1 при наличии сигнала и 0 при
его отсутствии;
s(t ) – огибающая сигнала;
n(t ) – белый гауссовский шум;
a,  – случайные амплитуда и начальная фаза.
82
Пусть случайная амплитуда сигнала имеет плотность вероятности
распределения по закону Релея:
 a2 
a
W ( a )  2 exp   2  ,
 2 
а
а

где амплитуда a  0 .
Случайная начальная фаза  , как и ранее, имеет равномерный закон
распределения на интервале   0,2π , с плотностью вероятности
1
распределения W ()  .
Для рассматриваемого случая безусловное
2π
отношение правдоподобия можно получить путем усреднения исходного по
случайным параметрам a и 
2 
l (u )    l (u / a, )W (a )W ()dad ,
(2.24)
0 0
где условное отношение правдоподобия для гауссовской статистики белого
шума имеет вид

 2 T
1 T 2
l (u / a, )  exp 
u
(
t
)
s
(
t
,
a
,
)
dt
s
(
t
,
a
,
)
dt



(2.25)
.


N
N
00

 00
Подставляя W () , W (a ) , выражение (2.25) в (2.24), и производя операции
интегрирования, имеем:
 22а Z12 
N0
(2.26)
l (u ) 
exp 
 ,
N0  E
N
N
E
(

)

 0 0
где E  2 E12а – средняя энергия сигнала;
1T 2
E1   s (t , a, )dt – энергия сигнала при a  1 ;
20
N 0 – спектральная плотность мощности белого гауссовского шума;
2
2
T

T

Z
2
2
Z1   z1  z2    u(t ) s(t ) cos 0tdt     u(t ) s(t ) sin 0tdt  –
a
0

0

корреляционный интеграл.
Отношение правдоподобия (2.26) является монотонной функцией
корреляционного интеграла, поэтому его можно сравнивать с порогом
обнаружения в соответствии с алгоритмом работы оптимального
обнаружителя:
83
H1
 
T
 T
Z0 .
(2.27)
  u(t ) s(t ) cos 0tdt     u(t ) s(t ) sin 0tdt 


0
 0
H0
Выражение (2.27) дает алгоритм работы оптимального обнаружения сигнала
со случайной амплитудой и начальной фазой на фоне аддитивного белого
гауссовского шума. На рис. 2.6 представлена структурная схема оптимального
обнаружителя.
2
2
Рис. 2.6
Устройство обнаружения, как и в случае обнаружителя сигнала со
случайной начальной фазой, представляет собой квадратурный приемник.
В приемном устройстве осуществляется умножение входного сигнала на
квадратурные гармонические сигналы на несущей частоте, их интегрирование,
возведение в квадрат, извлечение квадратного корня и сравнение с порогом Z 0
.
Произведем оценку качества работы обнаружителя сигнала со
случайной амплитудой и начальной фазой.
2.8. Характеристики обнаружения сигнала со случайной амплитудой
и начальной фазой
Произведем оценку качества работы оптимального обнаружителя
сигналов сослучайной амплитудой и начальной фазой на фоне белого
гаусовского шума.
В случае отсутствия сигнала в принимаемом сигнале на интервале
наблюдения на входе прогогового устройства шум имеет плотность
вероятности распределения по закону Релея:
 Z12 
Z1
(2.28)
W Z1 H 0   2 exp   2  .
 2 
1
1

84
EN
где обозначено 12  1 0 – дисперсия шума на входе порогового устройства.
2
Выражение (2.28) позволяет найти вероятность ложной тревоги для заданного
значения порога Z 0 :

 Z 
F   W Z1 H 0 dZ1  exp   02  .
(2.29)
 2 

Z0
1
В случае присутствия сигнала в принимаемом колебании на входе
оптимального обнаружителя условная плотность вероятности распределения
сигнала перед пороговым устройством распределена по закону Релея-Райса:
 Z12  a 2 E12   Z1aE1 
Z1
I0 
,
(2.30)
W Z1 H1, a   2 exp  
2
  2 


1
2
1
  1 

где I 0 ( x ) – модифицированная функция Бесселя нулевого порядка.
Выражение (2.30) усредним по случайной амплитуде входного сигнала,
имеющее релеевское распределение:
2


2 Z1
Z
1
.

(2.31)
exp
W Z1 H1  
2 2
2 2

N 0 E1  2a E1
 N 0 E1  2a E1 
Интегрируя выражение (2.31) получим вероятность правильного
обнаружения сигнала со случайной амплитудой и начальной фазой при
наличие порога обнаружения Z 0 :

2


Z
0
.
(2.32)
D   W Z1 H1 dZ1  exp  
 N E 1  2 2 E 2 N 
Z0
a 1
0 1
0 

Выражения (2.29) и (2.32) позволяют расчитать характеристики обнаружения
сигнала со случайной амплитудой и начальной фазой. При a  1 и 2a  0,5 эти
выражения связывает между собой простое соотношение:

DF
1
1 E1 N 0

1
2
 F 1 q 2 ,
(2.33)
2 E1
– отношение сигнал/шум.
N0
Последнее выражение (2.33) позволяет провести расчет и построение
характеристик обнаружения сигналов со случайной амплитудой и начальной
фазой, показанных на рис.8.5.
где q 
85
Рис.2.7
Из них видно, что в отличие от характеристик обнаружения со случайной
начальной фазой для заданного значения ложной тревоги F , наблюдается
проигрыш в отношении сигнал/шум для больших вероятностей правильного
обнаружения.
Рис.2.8
На рис. 2.8 построены характеристики обнаружения для сигнала со
случайной начальной фазой и со случайной амплитудой и начальной фазой
при вероятности ложной тревоги F  106 . Из графика видно, что потери в
отношении сигнал/шум для D  0,5 увеличиваются примерно в два раза 6/3≈2,
т.е. ~6дб. Значит для компенсации этих потерь необходимо поднять мощность
передатчика РЛС в два раза.
86
2.9. Согласованный фильтр
Корреляционный приемник не является единственным видом реализации
алгоритма оптимальной обработки (обнаружения) сигнала на фоне белого
гауссова шума (БГШ). В радиолокационных и других системах типичной
ситуацией является отсутствие информации о моменте появления сигнала на
входе приемного устройства. При неизвестном моменте прихода сигнала t3
для его обнаружения корреляционный приемник должен быть
многоканальным по запаздыванию. В этом случае увеличиваются
аппаратурные затраты пропорционально количеству каналов приемного
устройства. Поэтому на практике вместо многоканального во времени
корреляционного устройства часто применяют согласованный фильтр (СФ).
Пусть на вход обнаружителя на временном интервале наблюдения
t  [0, T ] действует аддитивная смесь детерминированного сигнала s(t ) и
белый гаусовский шум спектральной плотности мощности N 0 :
u(t )  s(t )  n(t ) .
Ранее было показано, что оптимальным обнаружителем такого сигнала
является
корреляционный
приемник,
выполняющий
вычисление
корреляционного интеграла вида:
2 T
Z
(2.34)
 u(t ) s(t )dt
N0 0
и сравнение его с порогом обнаружения.
Фильтр, выполняющий операцию вычисления корреляционного
интеграла (2.34) независимо от временного запаздывания сигнала называется
согласованным с сигналом s(t ) .
Покажем, что фильтр, имеющий импульсную характеристику
g (t )  k0 s(t0  t ) ,
(2.35)
где k0 ,t0 – постоянные, выполняет инвариантно во времени операцию
вычисления корреляционного интеграла (2.34).
Пусть на вход фильтра, показанного на рис. 2.9, который далее будем
называть согласованным, с импульсной характеристикой (2.35) поступает
сигнал uвх (t )
Рис. 2.9
Найдем выходной сигнал uвых (t ) , как свертку входного сигнала и импульсной
характеристики (2.35) через интеграл Дюамеля:
87
t
uвых (t )   uвх (t ) g (t  t )dt  .
(2.36)

Подставляя в (2.36) импульсную характеристику (2.35) и учитывая, что
g (t  t )  k0 s(t  t   t0 ) , получим на выходе СФ:
t
t
uвых (t )   uвх (t ) g (t  t )dt   k0  uвх (t ) s(t   t  t0 )dt  .

(2.37)

В соответствии с выражением (2.37) на выходе СФ с точностью до
постоянного множителя k 0 вычисляется взаимно корреляционная функция
входного процесса uвх (t ) и сдвинутого во времени сигнала s(t ) . В момент
2
времени t  t0 , для k0 
выходное значение напряжения равно:
N0
t
2 0
(2.38)
uвых (t0 ) 
 uвх (t )s(t )dt  Z .
N0 0
Проделанный анализ показывает, что на выходе СФ выполняется
операция вычисления корреляционного интеграла не зависимо от временного
положения входного сигнала.
По определению, согласованным фильтром сигнала s(t ) называется
фильтр, импульсная характеристика которого с точностью до постоянного
коэффициента k 0 является зеркальным отображением (относительно оси
ординат) сигнала s(t ) , сдвинутого по временной оси вправо на величину t0 .
Найдем ограничения на временное запаздывание t0 .
Пусть сигнал s(t ) имеет вид, показанный на рис. 2.10 сплошной линией
на временном интервале t  [ tн , tк ] . Для построения импульсной
характеристики
Рис.2.10
88
СФ построим зеркальное отображение этого сигнала s( t ) относительно оси
ординат, показанное на рисунке тонким пунктиром. Построим импульсную
характеристику СФ для частного случая k0  1 . Для этого сдвинем зеркально
отображенный сигнал s( t ) по оси времени вправо на величину t0 . По
определению импульсная характеристика фильтра является откликом
выходного сигнала на входное воздействие в виде uвх (t )  (t ) в момент
времени t  0 . Исходя из условия физической реализуемости, отклик не может
начаться ранее входного воздействия. Поэтому временной сдвиг t0  tк не
может начаться ранее окончания входного сигнала s(t ) .
Проведенный анализ показывает, что для обнаружения сигнала с
неизвестным временным запаздыванием в аддитивной смеси с шумом вместо
корреляционного приемника может быть использован СФ (см. рис. 2.9).
Рис. 2.11
На выходе СФ в момент времени t0  tк происходит вычисление
корреляционного интеграла Z , которое поступает на устройство сравнения с
порогом обнаружения Z 0 .
2.10. Частотная характеристика СФ
Пусть обнаруживаемый сигнал s(t ) имеет спектральную плотность вида:

S ( j)   s(t ) exp(  jt )dt  S () exp[ j()] ,
(2.39)

где S () – амплитудный спектр сигнала;
() – фазовый спектр сигнала.
Найдем комплексный коэффициент передачи
преобразование от его импульсной характеристики:
СФ
как
Фурье-

K ( j)   g (t ) exp(  jt )dt  K () exp[ j()] .

(2.40)
Подставим в (2.40) выражение для импульсной характеристики СФ (2.35),
получим
89

K ( j)  k0  s(t0  t ) exp(  jt )dt .

Перейдем к новой переменной t   t0  t в выражении под интегралом

K ( j)  k0 exp(  jt0 )  s(t ) exp( jt )dt   k0 exp(  jt0 ) S  ( j) ,
(2.41)


где S ( j)  S () exp[  j()] – комплексно-сопряженный спектр сигнала s(t )
. Подставляя в выражение (2.41) выражение (2.39) и приравнивая
действительные и мнимые части полученных выражений, получим:
 K ( )  k0 S ( )
.
(2.42)

( )  [( )  t0 ]
Из (2.42) видно, что передаточная функция СФ с точностью до
постоянного множителя k 0 совпадает с амплитудным спектром сигнала, а
фазо-частотная характеристика (ФЧХ) СФ с обратным знаком совпадает с
фазовым спектром сигнала и имеет временное запаздывание на время t0 на
выходе СФ.
Физический смысл первого равенства выражения (2.42) – передача на
выход СФ наиболее интенсивных частотных компонент сигнала. Последнее
утверждение можно интерпретировать как: «поддерживаем сильных».
Второе равенство выражения (2.42) t0  [( )  ( )] говорит о том,
что в момент времени t0 вычисления корреляционного интеграла Z в СФ
происходит компенсация временных задержек спектральных компонент
сигнала и их синфазное суммирование. В результате этого на выходе СФ
появляется сигнал, амплитуда которого пропорциональна сумме спектральных
составляющих входного колебания s(t ) .
2.11 Свойства согласованного фильтра
1. Найдем отношение сигнал/шум на выходе СФ в момент максимума
сигнала на его выходе t  t0 . Из выражения (2.38) имеем:
t0
 t0 2


uвых (t0 )  k0  [ s(t )  n(t )]s(t )dt  k0  [ s (t )dt   n(t ) s(t )dt  .
(2.43)


0
0
0

Первый интеграл пропорционален энергии входного сигнала uвых (t0 )  k0 Ec .
Второй интеграл соответствует флюктуационной (шумовой) компоненте БГШ.
Мощность (дисперсию) флюктуационной компоненты найдем в виде:
t0
90
t t


N
 200

  M k0   n(t )n(t ) s(t ) s(t )dtdt   k02 0 Ec ,
2


 00

t


0
 N
с учетом того, что M   n(t )n(t  )dt   0 ( ) – АКФ БГШ. Отношение


0
 2
сигнал/шум на выходе СФ для произвольного сигнала равно:
u (t )
2 Ec
.
(2.44)
q  вых 0 

N0
Отношение сигнал/шум на выходе СФ не зависит от формы сигнала, а
определяется его энергией и спектральной плотностью мощности шума.
2. Покажем, что отношение сигнал/шум на выходе согласованного
2 Ec
фильтра максимально и равно q 
по сравнению с любым другим
N0
фильтром с передаточной функцией K ( j) . Пусть на вход фильтра с
произвольным коэффициентом передачи K ( j) поступает сигнал со
спектральной плотностью S ( j) и БГШ со СПМ N 0 . Найдем отношение
сигнал/шум на выходе такого фильтра:
u (t )
q  вых 0 .

Для максимума сигнала на выходе фильтра имеем:
1 
uвых (t0 ) 
(2.45)
 S ( j) K ( j) exp( jt )d .
2  
Мощность шума на выходе фильтра равна:
N0 1 
2
2
 
K ( j) d .

2 2  
Применим к выражению (2.54) неравенство Шварца-Буняковского:


 
2
2 

F
(
x
)
(
x
)
dx
F
(
x
)
dx
(
x
)
dx .










Тогда для отношения сигнал/шум на выходе фильтра получим:
2

2
 S ( j) d
2 Ec
.
N0 2
N0
Таким образом, любой другой фильтр, отличающийся от СФ, дает на
выходе отношение сигнал/шум меньшее, чем согласованный.
q  q0 


91
3. Форма сигнала на выходе СФ без шума с точностью до постоянного
множителя k 0 совпадает с его АКФ сдвинутой на время длительности сигнала
tc  t0 .
Для проверки нашего утверждения найдем сигнал на выходе СФ, как
свертку входного сигнала с ИХ согласованного фильтра. Из выражения (2.37)
получим:
t
t


uвых (t )   uвх (t ) g (t  t )dt  k0  s(t ) s(t   t  t0 )dt  k0 R(t  t0 ) ,
t
где R( )   s(t ) s(t   )dt  – АКФ сигнала s(t ) .

Таким образом, видно, что сигнал без шума (с малым уровнем шума) на
выходе СФ с точностью до постоянного множителя совпадает с его АКФ
сдвинутой вправо по оси абсцисс на время длительности сигнала.
2.12 Обнаружение пачек импульсных сигналов
Сигнал, отраженный от точечной цели обзорной РЛС кругового режима
работы представляет собой пачку радиоимпульсов, модулированных
диаграммой направленности антенны F 2 () (за счет двукратного
распространения до цели и обратно) в азимутальной плоскости. Пусть антенна
РЛС имеет ширину диаграммы направленности  и вращается равномерно со
скоростью  об/мин. Примем, что время облучения главным лепестком
диаграммы направленности антенны равно T0    , а период следования
зондирующих импульсов T1 . Тогда на входе приемного устройства РЛС
принимается пачка из N  T0 T1   T1 импульсов.
В зависимости от назначения РЛС пачка из N импульсов может
обладать свойством когерентности. Импульсы когерентны, если начальные
фазы отдельных импульсов несущего колебания одинаковы, или изменяются
по детерминированному закону. В противном случае начальные фазы
импульсов являются случайной величиной, а сама пачка является
некогерентной. В приемном устройстве РЛС возникает задача обнаружения
пачки импульсов.
2.13. Когерентный обнаружитель пачки импульсов
Пусть на вход обнаружителя поступает аддитивная смесь когерентной
пачки из N импульсов с весами ki и шум. СФ такого сигнала имеет ИХ,
зеркально отображенную относительно оси ординат и сдвинутую вправо на
92
длительность пачки. Весовые коэффициенты СФ ki будут располагаться в
обратном порядке. На рис. 2.12 представлена структура СФ.
Рис. 2.12
Она состоит из последовательного соединения СФ для парциального
радиоимпульса СФ0 и согласованного фильтра на пачку импульсов СФN,
суммируемых с учетом их весов ki с точностью до начальных фаз
гармонического заполнения отдельных импульсов.
СФ0 с прямоугольной огибающей может быть реализован из
последовательного соединения высокодобротного резонансного усилителя
(ВРУ), радиочастотной линии задержки ЛЗ0 на длительность импульса и
вычитающего устройства с точностью до начальной фазы частоты заполнения
импульса. Нетрудно видеть, что при подаче на такое устройство дельтаимпульса на его выходе формируется парциальный импульсный сигнал.
СФN представляет собой трансверсальный (весовой) фильтр. Его
структурная схема представлена на рис.2.13.
Рис. 2.13
Он состоит из линии задержки ЛЗ0 с отводами на время запаздывания
периода повторения зондирующих импульсов, весовых коэффициентов ki и
сумматора.
Техническая реализация такого устройства представляет собой
достаточно сложную задачу, поскольку суммирование парциальных
импульсов осуществляется на радиочастоте с точностью до фазы
гармонического сигнала. На практике, как правило, начальная фаза входного
сигнала неизвестна, поэтому когерентную обработку пачки импульсов делают
на видеочастоте в квадратурном приемнике (см. рис.2.14).
93
Рис. 2.14
Накопитель в приемнике (НАК) представляет собой последовательное
соединение СФ0 и СФN на видеочастоте, что существенно упрощает процесс
обработки сигнала.
Когерентное накопление пачки из N импульсов c прямоугольной
огибающей увеличивает отношение сигнал/шум. Так, если отношение
сигнал/шум по одному импульсу q0 , то при накоплении пачки оно равно
qN  q0 N . Последнее можно объяснить тем, что импульсы пачки
суммируются по амплитуде, а шум по мощности. Платой за такое увеличение
сигнальной компоненты выражается в существенном усложнение устройства
обработки.
2.14 Некогерентный обнаружитель пачки импульсов
Пусть на вход приемного устройства РЛС поступает некогерентная пачка
из N импульсов. Начальные фазы импульсов неизвестны и случайны.
Обработка таких импульсов возможна после выделения их огибающей путем
последетекторного накопления. Поскольку детектор является нелинейным
элементом, то такая обработка сигналов приводит к потерям в отношении
сигнал/шум по сравнению с когерентной.
Для некогерентной пачки радиоимпульсов со случайной начальной
фазой отношение правдоподобия можно представить в виде произведения
отдельных отношений правдоподобия для каждого импульса, поскольку они
статистически независимы. Тогда отношение правдоподобия пачки имеет вид:
N
l (u )   li (u ) ,
i 1
(2.46)
где li (u ) – безусловное отношение правдоподобия для одиночного импульса
со случайной начальной фазой. Для случая гауссовской статистики помехи
имеем
 E   2Z 
li (u )  exp   i  I 0  i  ,
(2.47)
N
N
0  0 

94
где Ei – энергия парциального импульса;
t 
2 i
Zi 
 u(t ) si (t )dt – корреляционный интеграл в момент максимального
N0 t
i
значения на выходе СФ i-го импульса.
В соответствии с оптимальным алгоритмом работы обнаружителя пачки
радиоимпульсов отношение правдоподобия (2.46) сравнивается с порогом
обнаружения. После подстановки в (2.46) выражения (2.47) и его
логарифмирования имеем:
H1
N
 2 Zi  
I
ln
(2.48)
 0   Z 0 ,

N
 0
i 1
H0
где Z 0 – порог обнаружения. Учитывая монотонность логарифмической и
функции I 0 () , с порогом обнаружения можно сравнивать суммы
корреляционных интегралов импульсов:
N

(2.49)
Z
 i Z0 .

i 1
Структурная схема обработки имеет вид, показанный на рис. 2.15.
Рис. 2.15
В соответствии с алгоритмом (2.49) осуществляется согласованная фильтрация
одиночных импульсов, выделение их огибающей, суммирование максимумов
выходных значений и сравнение суммы с порогом.
Оптимальная характеристика детектора огибающей импульсов
выбирается из аппроксимации нелинейного преобразования функции:
 x 2 4 , для x  1
ln I 0 ( x )  
.
(2.50)

,
для
1
x
x

Из выражения (2.50) видно, что для сигналов с малым отношением
сигнал/шум детектор должен быть квадратичным, а для сигналов с большим
отношением – линейным.
95
Можно показать, что накопление импульсных сигналов пачки из N
импульсов неэффективно при отношении сигнал/шум по одиночному
импульсу q0  1 . Потери в накоплении таких сигналов   N .
2.15. Накопитель пачки импульсов с логикой «k из N»
Пусть на входе обнаружителя наблюдается аддитивная смесь пачки из N
некогерентных радиоимпульсов с прямоугольной огибающей и БГШ. Найдем
вероятность правильного обнаружения и ложной тревоги обнаружителя пачки
сигналов с логикой «k из N». Структурная схема обнаружителя показана на
рис.2.16.
Рис. 2.16
Он состоит из СФ0 на одиночный импульс пачки, бинарного квантователя (БК)
с порогом квантования Z 0 по одиночному импульсу. На выходе БК появляется
сигнал единицы, если входной сигнал превышает порог Z 0 и ноль в противном
случае. Логический обнаружитель принимает решение о наличие пачки, если
порог обнаружения превышает не менее k входных импульсов, в противном
случае принимается решение о её отсутствии.
Поскольку вместо последетекторного накопителя в устройстве применен
более простой логический обнаружитель в нем появляются дополнительные
по сравнению с некогерентным накопителем потери в отношении сигнал/шум.
Пусть вероятность ложной тревоги на входе БК равна F0 . Тогда вероятность
того, что k входных импульсов пачки одновременно превысят порог БК,
равна:
k k
F  CN
F0 (1  F0 ) N  k ,
(2.51)
N!
– биномиальный коэффициент равный числу сочетаний
k!( N  k )!
из N импульсов пачки по произвольным k импульсам. Решение о ложной
тревоге пачки импульсов принимается, так же, если превышение произошло
для n  k импульсам:
где CNk 
N
k k
F   CN
F0 (1  F0 ) N  k .
k n
96
(2.52)
Выражение (2.52) дает суммарную вероятность ложной тревоги
логического обнаружителя. В соответствии с критерием обнаружения
Неймана-Пирсона, по заданной вероятности ложной тревоги F обнаружителя
выбирается порог бинарного квантователя Z 0 .
Найдем вероятность правильного обнаружения пачки некогерентных
импульсов логического обнаружителя. Пусть вероятность правильного
обнаружения одиночного импульса пачки равна D0 . Тогда вероятность того,
что k импульсов пачки одновременно превысят порог БК, равна:
D  C Nk D0k (1  D0 ) N  k .
(2.53)
Решение об обнаружении пачки импульсов принимается, если порог БК
превышает n  k входных импульсов:
N
k k
D   CN
D0 (1  D0 ) N  k .
(2.54)
k n
Выражения (2.52) и (2.54) позволяют найти вероятности ложной тревоги
и правильного обнаружения логического устройства и построить
характеристики обнаружения.
Анализ полученных формул показывает, что для заданного значения
импульсов пачки N существует оптимальное значение числа обнаруживаемых
импульсов k , для которых потери в отношении сигнал/шум по сравнению с
оптимальным некогерентным накопителем будут минимальными. Найденное
3
значение равно k 
N . Возникающие при этом потери малы и не
2
превышают величины ~1дб.
2.16 Обнаружитель сигналов на фоне небелого шума
Пусть на вход радиолокационного обнаружителя сигналов поступает
аддитивная смесь и гауссовского шума
u(t )  s(t )  n(t ) ,
(2.55)
где s(t ) – детерминированный сигнал;
n(t ) – гауссовский шум с известной АКФ K n () .
Параметр  может принимать два дискретных значения:
 1, сигнал есть
.

0,
сигнала
нет

Входной процесс на интервале наблюдения t  [0, T ] представлен своими
выборочными значениями с интервалом дискретизации в соответствии с
теоремой Котельникова. На этом интервале входной процесс (2.55) с
t  ti  ti 1 для i  [1, m] представим в виде:
97
(2.56)
U  S  N ,
где U  (u1, u2 ,..., um ), S  ( s1, s2 ,..., sm ), N  ( n1, n2 ,..., nm ) – вектор-столбцы
выборочных значений смеси, сигнала и шума. АКФ шума представим в виде
прямоугольной размера (m  m) корреляционной матрицы R n .
В соответствии с ранее рассмотренным правилом, оптимальный
обнаружитель детерминированного сигнала на фоне гауссовского шума
должен вычислить отношение правдоподобия и сравнить его с порогом
обнаружения
H1
W ( U / H1 ) 
l (U) 
l0 .
(2.57)
W (U / H 0 ) 
H0
Условные плотности вероятности выборочных значений входного процесса
для гауссовской статистики при отсутствии и наличии сигнала,
соответственно, имеют вид:
1
 1 T 1 
(2.58)
exp
W (U / H 0 ) 
  U Rn U  ,
1
2
(2) m 2 R n
 2

1

 1
1
T
(2.59)

(

)
(

)
exp
W (U / H 1 ) 
U
S
R
U
S
,

1
2
n
m2
2
(2) R n


где R n – определитель матрицы R n ;
R n1 – матрица обратная матрице R n ;
(U  S)T – транспонированный вектор-столбец (вектор-строка) разности
отсчетов входной смеси и сигнала.
Подставим выражения (2.58) и (2.59) в отношение правдоподобия (2.57)
и получим
 1
 H1
exp   (U  S) T R n1 (U  S) 
 2
  l.
l (U) 
(2.60)
0

 1 T 1 
exp   U R n U 

 2
H0
Прологарифмируем и преобразуем обе части выражения (2.60), получим:
H1

1 T 1
S R n U  U T R n1S  S T R n1S  ln l0 .
(2.61)

2
H0
98
Учтем, что АКФ матрицы гауссовского шума R n и R n1 являются
симметричными, обладают свойством R n R n1  I n , где I n – единичная матрица,
выражение (2.61) с учетом того, что S T R n1U  U T R n1S , можно представить в
виде:
H1
 
S T R n1S 
T
1
U R n S  ln l0 
(2.62)
  Z0 ,
 
2 
H0
где Z 0 – порог обнаружения, поскольку S T R n1S является скаляром и не
зависит от входного процесса u(t ) .
Из выражения (2.62) следует алгоритм работы оптимального
обнаружения детерминированного сигнала на фоне коррелированного
гауссовского шума. На рис. 2.17 показана структурная схема обнаружителя.
Рис. 2.17
Алгоритм работы обнаружителя заключается в вычислении
корреляционного интеграла Z  U T R n1S и сравнения его с порогом
обнаружения Z 0 . В случае превышении порога обнаружения порогового
устройства (ПУ) принимается решение о наличии сигнала в принимаемой
смеси (гипотеза H1 ). В противном случае принимается решение об отсутствии
сигнала на входе обнаружителя (гипотеза H 0 ).
Алгоритм работы обнаружителя может быть реализован с помощью так
называемого «обеляющего» фильтра. Известно, что если корреляционная
матрица R n1 является симметричной, то её можно представить в виде
произведения двух нижних треугольных матриц V T и V той же размерности:
(2.63)
R n1  V T V .
Алгоритм обнаружения (2.62) с учетом (2.63) имеет вид
99
H1

( U T V T )( VS )  UTVS V
Z0 ,

H0
(2.64)
где U TV  U T V T и S V  VS – два матричных фильтра, осуществляющих
предварительную обработку входной смеси и сигнала перед сравнением их
произведения с порогом обнаружения. Структурная схема обработки показана
на рис. 2.18.
Рис. 2.18
Выясним смысл предварительного преобразования входной смеси и
сигнала. Если на входе обнаружителя присутствует только один шум, то это
приводит к его обелению (декорреляции входных отсчетов) перед матричным
умножителем. Найдем корреляционную матрицу шума на входе умножителя:
R V  M N V N TV   VM NN T V T  VR n V T  V(V T V) 1 V T  I ,
 - операция статистического усреднения отсчетов;
где M 
I – единичная матрица размера ( m  m) .
Входные фильтры V T и V осуществляют декорреляцию входных
отсчетов шума и преобразование входного сигнала. Матричный умножитель
производит операцию умножения и суммирования входных отсчетов
эквивалентную операции вычисления корреляционного интеграла в
непрерывной системе обнаружения. Особенность обработки на фоне
коррелированного шума заключается в преобразовании обнаруживаемого
сигнала и взаимно-корреляционной обработки входного процесса с
преобразованным сигналом.
Поясним эти процессы в случае непрерывных сигналов в частотной
области. Пусть на вход обнаружителя поступает аддитивная смесь,
детерминированного сигнала S ( j) и коррелированного шума, с
неравномерной по частоте спектральной плотности мощности Gn () .
Предположим, что энергетический спектр шума не обращается в ноль в
100
интересующем нас диапазоне частот. Найдем передаточную функцию
2
обеляющего фильтра в виде Gn ( ) KV ( j)  const , откуда
C
2
KV ( j) 
,
Gn ( )
где С  const .
Найдем
спектр
сигнала
после
обеляющего
фильтра
SV ( j)  S ( j) KV ( j) . Передаточная функция СФ для сигнала SV ( j) на
фоне обеленного шума без учета фазового множителя имеет вид:
K0 ( j)  k0 S  ( j) KV ( j) .
Найдем передаточную функцию СФ обнаружителя сигнала S ( j) на фоне
коррелированного шума как произведение обеляющего и согласованного
фильтров
K ( j)  KV ( j) K0 ( j) 
S  ( j) .

 k0 S ( j) KV ( j) KV ( j)  k 
Gn ()

(2.65)
Из выражения (2.65) видно, что СФ обнаружителя сигнала на фоне
некоррелированной помехи выполняет две основные операции – отбеливание
спектра входной помехи (функция знаменателя) и накопление составляющих
спектра входного сигнала (функция числителя).
2.17 Различение двоичных детерминированных сигналов
Передача
информации
часто
осуществляется
поочередно
детерминированными (т.е. точно известными) сигналами si(t), где i = 1, 2, …,N,
которые принимаются на фоне шума. При этом возникает задача различения
этих сигналов, т.е. задача установления того, какой именно сигнал
принимается. Поскольку это различение производится на фоне случайного
шума n(t), то задача различения является статистической.
Если используются лишь два сигнала s1(t) и s2(t), т.е. сигналы являются
двоичными, то принимаемое колебание можно представить в виде суммы
u(t) = θs1(t) + (1 –θ)s 2(t) + n(t),
где  – параметр различения сигналов, равный 1 при наличии первого сигнала
и 0 при наличии второго сигнала. По принятой реализации входного
колебания u(t) необходимо выяснить, какой из двух возможных сигналов
присутствует в указанной реализации, т.е. определить величину ̂ .
В качестве критерия оптимальности будем использовать критерий
«идеального наблюдателя», который заключается в минимизации вероятности
суммарной ошибки:
101
Pош = {P(s1)P(s2/s1) + P(s2)P(s1/s2)}min,
где P(s1) и P(s2) – априорные вероятности присутствия каждого из сигналов в
принимаемом колебании (они считаются известными, а их сумма равна
единице), а P(s2/s1) и P(s1/s2) – условные вероятности ошибочных решений о
наличии каждого из сигналов (они иногда называются вероятностями
перепутывания сигналов).
Ранее было получено, что оптимальный алгоритм различения
сигналов в сответствии с критерем «идеального наблюдателя» (см. выражение
2.9), заключается в вычислении отношения правдоподобия l(u) и сравнении
его с порогом l0 = P(s2)/P(s1). Решения о наличии сигнала s1(t) или s2(t) в
принимаемом колебании u(t) осуществляется по правилу
W u s1 
l (u ) 
 l0 – присутствует сигнал s1(t),
W u s2 
(2.66)
W u s1 
l (u ) 
 l0 – присутствует сигнал s2(t),
W u s2 
где W u s1  − условная плотность вероятности распределения смеси сигнала и
шума u(t) при наличии в ней сигнала s1(t);
W u s2  − условная плотность вероятности распределения принимаемой смеси
сигнала и шума u(t) при наличии в ней сигнала s2(t).
Входной шум n(t) полагаем белым гауссовским со спектральной
плотностью мощности (энергетическим спектром), равной G(f) = N0 для f  0
. Функционал плотности распределения вероятности отрезка гауссовского
«белого» шума n(t) на временном интервале [0,T] имеет вид:
 1 T 2

W n(t )   k exp 
n (t )dt  ,
(2.67)

N
0


0
где k – нормирующий множитель. Подставим выражение (2.67) в отношение
правдоподобия (2.66):
 1 T

u (t )  s1 (t )2 dt 
k exp 

N0 0
 2 T
E1  E2 







exp
(
)
(
)
(
)
l (u ) 
u
t
s
t
s
t
dt

.
1
2

N0 0
N0 
 1 T

2

k exp 
 u (t )  s2 (t ) dt 
 N0 0

Преобразуем полученный оптимальный
детерминированных сигналов (2.66) к виду:
102
алгоритм
различения
двух
s1

E  E2   
exp  Z  1
   l0 ,
N

0

s2
где l0 
P s 2 
– порог различения сигналов;
Ps1 
2 T
Z
u t s1 t   s2 t dt – значение функции взаимной корреляции между

N0 0
принимаемым колебанием и разностью ожидаемых сигналов (корреляционный
интеграл);
T
Ei   si2 t dt – энергия i-го сигнала (i =1 или 2).
0
Учтем, что экспоненциальная функция монотонно возрастает
относительно своего аргумента, поэтому с порогом можно сравнивать её
аргумент. Найдем логарифм отношения правдоподобия и получим следующее
выражение для алгоритма оптимального различения сигналов:
s1

( E  E2 )
Z ln [ P( s1 ) P( s 2 )]  1
,
(2.68)

N0
s2
где Z 0  ln [ P( s1 ) P ( s 2 )]  ( E1  E2 ) / N 0 – порог различения сигналов.
Из этого алгоритма следует, что оптимальный различитель сигналов
должен вычислять значение функции взаимной корреляции Z и сравнивать
его с порогом различения l0.
Следовательно, структурная схема оптимального различителя двух
детерминированных сигналов состоит из взаимно корреляционного (ВКУ) и
порогового устройств. На входы ВКУ поступают соответственно принимаемое
колебание и разность ожидаемых сигналов. В пороговом устройстве
происходит сравнение выходного сигнала ВКУ с уровнем порога Z0 (рис. 1а).
На выходе ПУ вырабатывается окончательное решение о приеме первого
сигнала s1(t) при Z > Z0 или о приеме второго сигнала s2(t) при обратном
соотношении Z < Z0.
103
Рис. 2.19
Очевидно, что ВКУ, управляемый разностью ожидаемых сигналов (рис.
2.19,а), эквивалентен параллельному соединению двух ВКУ, управляемых
соответственно первым и вторым сигналами, и вычитающему устройству их
выходных напряжений (рис. 2.19,б). Верхний и нижний корреляторы могут
быть заменены согласованными фильтрами с импульсными характеристиками,
согласованными с первым и вторым сигналами соотвнтственно.
Если априорные вероятности ожидаемых сигналов одинаковы:
Р(s1) = Р(s2) = 0,5, как и их энергии: Е1 = Е2 = Е, то такая система передачи
сигналов называется бинарной симметричной. У нее уровень порога Z0 = 0 и
алгоритм оптимального различения упрощается:
s1

Z 0.
(2.69)

s2
Далее для простоты будем рассматривать симметричные бинарные системы
передачи информации.
2.18. Характеристики оптимального различения сигналов
Найдем суммарную ошибку различения двух бинарных симметричных
сигналов. Как следует из предыдущего изложения, вероятность суммарной
ошибки равна
Pош  0,5P( s2 s1 )  P( s1 s2 ) ,
где Р(s2/s1) и Р(s1/s2) – вероятности перепутывания сигналов. Очевидно,
перепутывание сигналов s1 на сигнал s2, когда при приеме первого сигнала
выносится ошибочное решение о приеме второго сигнала, происходит, если
напряжение u1 на выходе ВКУ (рис. 2.19,а) при действии на его вход суммы
первого сигнала и шума будет меньше нулевого порогового уровня u1 < 0.
Поэтому
0
P s2 / s1   P u1  0   W (u1 / s1 )du1 ,

104
где W(u1/s1) – условная плотность вероятности напряжения u1 при наличии в
принимаемой смеси сигнала s1. Входной гауссовский процесс подвергается
линейному преобразованию, поэтому выходное напряжение u1 как сумма
выходного шума и выходного сигнала распределено также по гауссовскому
закону. Найдем статистические характеристики выходного процесса.
На выходе ВКУ получим:
2 T
nt   s1 t s1 t   s2 t dt  n1  m1 ,
u1 

N0 0
2 T
2E
1  r  – регулярная
m1 
s1 t s1 t   s2 t dt 

N0 0
N0
где
компонента
выходного случайного процесса (выходной сигнал);
1T
r   s1 t s2 t dt – коэффициент взаимной корреляции между первым и
E0
вторым сигналами;
T
n1   nt s1 t   s2 t dt
–
флюктуационная
компонента
выходного
0
случайного процесса (выходной шум), распределенная по гауссовскому
закону с нулевым математическим ожиданием m1{n1} = 0 и дисперсией
σ12 
4E
(1  r ) .
N0
Найдем ошибку перепутывания сигналов:
2


 E
 (u1  m1 ) 

, где






exp
1
(
1
)
r
Ps2 / s1  
du

 1



2
2
N


21
0


2  


x

1 0
 x2 

  x0  
exp  dx – интеграл вероятности.

2π  

 2 

E
– отношение сигнал/шум.
N0
1
0

Аналогично найдем вероятность P s1 / s2   P u1  0   W (u1 / s2 )du1 ,
0
где W(u1/s2) – условная плотность вероятности напряжения u1 при наличии в
принимаемой смеси сигнала s2.
Математическое ожидание выходного сигнала равно
105
2 T
2E






r  1;


m2 
s
t
s
t

s
t
dt


 2 1
2
N0 0
N0
дисперсия выходного процесса u1,
σ 22 
как и в предыдущем случае, равна
4E
(1  r ) .
N0
W(u1)
W(u1/s1)
W(u1/s2)
Р(s1/s2)
P(s2/s1)
0
u1
Рис. 2.20
На рис. 2.20
представлены условные плотности вероятности
распределений W(u1/s1) и W(u1/s2) и вероятности перепутывания сигналов.
Выходное напряжение u1 при наличии на входе сигнала s2 распределено по
гауссовскому закону с математическим ожиданием m2 и дисперсией 22 (рис.
2.20), вследствие чего
 u1  m2 2 
 E (1  r ) 
1 
.

P s1 / s2  
du



1
 exp 

1


N
2 πσ 2 0

2σ 22 
0


Тогда вероятность суммарной ошибки
 E (1  r ) 
.
Pош  0,5Ps2 / s1   Ps1 / s2   1  

N
0


(2.70)
Таким образом, вероятность суммарной ошибки, характеризующая
потенциальную помехоустойчивость при различении равновероятных
сигналов с одинаковыми энергиями, зависит только от отношения сигнал/шум
E
и коэффициента взаимной корреляции между двоичными сигналами r.
N0
Чем меньше величина коэффициента взаимной корреляции, тем меньше
вероятность ошибки и выше потенциальная помехоустойчивость. Наивысшая
потенциальная помехоустойчивость достигается при коэффициенте взаимной
корреляции rmin = – 1, когда сигналы противоположны: s1(t)= –s2(t). Такие
сигналы в радиотехнике различаются значениями начальных фаз на  и
поэтому называются фазоманипулированными (ФМн сигналами):
106
при t  (0, Т).
Для них
s1 (t )  s  cos ω0 t
,

s
t

s

t



s

t
(
)
cos(
ω
π
)
cos
ω
 2
0
0
 2E 
.
Pош.фм  1  

 N0 
(2.71)
Если сигналы манипулированны по частоте (ЧМн сигналы):
 s1(t )  s  cos ω1t
,

s2 (t )  s  cos ω2t
для t  (0, Т), то при 1  2 T  1 , коэффициент взаимной корреляции
приближенно равен нулю r  0 (ортогональные сигналы), и для них имеем
 E 
.
Pош. чм  1  

 N0 
(2.72)
На рис. 2.21 представлена зависимость вероятности ошибки различения в
зависимости от отношения сигнал/шум для бинарных сигналов с ФМн и ЧМн.
Рис.2.21
Третьим видом манипуляции сигналов является амплитудная (АМн):
 s1(t )  s  cos ω0t
, при t  (0, Т).

(
)

0
s
t
 2
107
Это так называемая передача сообщений с пассивной паузой. Она не
принадлежит к симметричной системе передачи. Как и при других видах
манипуляции, вероятность суммарной ошибки при АМ
Pош ам  0,5Ps2 / s1   Ps1 / s2 ,
где Р(s2/s1) – вероятность пропуска ненулевого сигнала s1(t), а Р(s1/s2) –
вероятность ложного решения о приеме сигнала s1(t).
Z0
Ps2 / s1   Pu1  Z 0    W (u1 / s1 )du1 ,

где u1 – напряжение на выходе ВКУ (рис. 2.19,а) при действии на его вход
суммы ненулевого сигнала и шума:
2 T
2 T
2E


























;
u1 
n
t
s
t
s
t
s
t
dt
n
t
s
t
s
t
dt
n


1
1
2
1
1
1
N0 0
N0 0
N0
T
где флюктуационная составляющая равна n1   nt s1 t dt .
0
Поскольку, как и выше, входной шум n(t) является «белым» гауссовским с
нулевым математическим ожиданием, то выходной шум n1 распределен тоже
по гауссовскому закону с нулевым математическим ожиданием m 
дисперсией  
2
2E
. Поэтому напряжение u1 имеет также гауссовский закон
N0
распределения выходных значений.
Вероятность ошибки при наличии сигнала s1(t) равна
Ps2 / s1  
где Z 0 
2E
и
N0
2
 
2E  
 
  u1 
Z
 E 
N
1
 
0  

,
exp
du
1




 1

2
2 


2
σ
2
N
2σ  
0 






0
E
– порог различения сигналов.
N0
108
Вероятность ошибки при отсутствии сигнала s1(t) равна

Ps1 / s2   Pu1  Z 0    W (u1 / s2 )du1 ,
Z0
где u1 – напряжение на выходе ВКУ. Напряжение на выходе ВКУ u1
представляет собой напряжение гауссовского шума. Вследствие этого
 E 
1 
 n12 
.

exp
1
Ps1 / s2  
dn




1
2 
2 



2σ Z
 2σ 
 2N0 
0
Тогда вероятность суммарной ошибки
 E 
.
Pош ам  1  

2
N
0 

Рис. 2.22
На рис. 2.22 представлена зависимость вероятности ошибок различения
для бинарных сигналов с АМн, ЧМн и ФМн. Сравнение вероятностей ошибок
при ФМн, ЧМн и АМн, отображаемых кривыми потенциальной
помехоустойчивости (рис. 2.22), показывает, что наибольшую потенциальную
помехоустойчивость обеспечивает ФМ, а наименьшую – АМ (с пассивной
паузой). Для получения одинаковой потенциальной помехозащищенности
энергия принимаемого сигнала при ЧМ может быть взята в 2 раза меньше, а в
случае ФМ – в 4 раза меньше, чем при АМ. Следует, однако, иметь в виду, что
в отличие от ФМ и ЧМ при АМ передаётся только один сигнал. Поэтому если
109
исходить из равных средних энергетических затрат, то системы различения с
ЧМ и АМ сигналами будут обладать одинаковой помехоустойчивостью.
2.19. Примеры
2.19.1. Обнаружение детерминированного сигнала
Пример 1
Сигнал на входе обнаружителя полностью известного сигнала является
колоколообразным импульсом
  t 2 
u(t )  U exp      ,
  и  


имеющим
амплитуду
U
и
длительность
τи/2
по
уровню
u и 
 2   exp      0,46 . Импульс может поступать на вход обнаружителя в


U
 4
виде аддитивной суммы с помехой в виде «белого шума» со спектральной
плотностью мощности N0 = 10– 17вт/гц.
Определить какое пороговое значение Z0 нужно установить на входе
порогового устройства, чтобы получить вероятность правильного
обнаружения D =0,95? Данные для решения задачи: U =1мкв, τи =2мкс.
Вероятность ложной тревоги F и правильного обнаружения D для
полностью известного сигнала имеют вид:
F  1  ( Zн )
D  1   ( Z н  q) ,

1 Z

 x2 
где  (Z) 
exp  dx – табулированный интеграл вероятности;

2  


 2
Z
Z н  0 – нормированный пороговый уровень;
q
2E
– отношение сигнал/шум;
q
N0
N0 – спектральная плотность мощности шума;
2




t
U 2 и
2


– энергия импульса.
E   U exp  2  dt 



2
 и 


110
2E
2 и
U
 5,32 на входе
N0
N0
обнаружителя детерминированного сигнала. Представим выражение для
вероятности правильного обнаружения в следующем виде:
1   ( Z н  q)   ( q  Z н )  0,95 .
Используя таблицу интеграла вероятности, находим аргумент интеграла
вероятности q  Z н  1,65 и значение порога обнаружения Z н  q  1,65  3,67 .
Найдем
отношение
сигнал/шум
q
Пример 2
Определить требуемое значение амплитуды U прямоугольного
видеоимпульса длительности и  0,1мкс , обнаруживаемого на фоне «белого
гауссовского шума» со спектральной плотностью мощности N 0  1018 вт гц ,
на входе приёмника с вероятностью пропуска сигнала Pпр  1  D  0,1 при
вероятности ложной тревоги F  105 .
Для обнаружителя детерминированного сигнала для заданного D=0,9
найдем по формуле D   ( q  Z н ) и таблицам интеграла вероятности
q  Z н  1,29 и требуемое значение отношения сигнал/шум q  Z н  1,29 .
Найдем значение нормированного порога Z н  4,75 для заданных
вероятностей ложной тревоги F  105 с использованием выражения
F  1  ( Zн ) .
Найдем необходимое значение отношения сигнал/шум по полученным
данным q  Z н  1,29  6 .
Определим значение амплитуды прямоугольного импульса U для
заданного τи и отношения сигнал/шум q:
2E
q
– отношение сигнал/шум на выходе СФ;
N0
E  U 2 и – энергия прямоугольного видеоимпульса.
Откуда можно получить U  q 
Пример 3
N0
 1,34 мкв.
2 и
Определить вероятность ошибки F «идеального наблюдателя» в
когерентном
приемнике,
который
обнаруживает
радиоимпульс с
111
колоколообразной
огибающей
вида
  t 2 
u(t )  U exp      ,
  и  


имеющий
u и 
2
 
амплитуду U и длительность τи/2 по уровню 
 exp     0,46 , на
U
 4
фоне теплового шума приёмника, имеющего шумовую температуру T оK.
Данные для решения задачи: U=1мкв, τи=0,1мкс, T о=3000К
При решении задачи принять, что спектральная плотность мощности шума
равна N 0  kT , где к= 1,38∙10-23 вт/гц – постоянная Больцмана, а
T оK шумовая температура приемника.
Вероятность ошибки различения детерминированного сигнала,
обнаруживаемого на фоне гауссовского шума в приемнике «идеального
наблюдателя» равна:
 E 
.
F  1  

2
N
0

Найдем энергию импульса с гауссовской огибающей
2




t
U 2 и
2


.
E   U exp  2  dt 



2
 и 


Определим спектральную плотность мощности шума N 0  kT .
Подставим найденные значения в выражение для вероятности ложной тревоги
и получим:
U
2и 
F  1  
 0,0018 .
2

kT


2.19.2. Воздействие сигнала и шума на СФ
Пример 4
На вход обнаружителя сигналов
поступает аддитивная смесь
прямоугольного видеоимпульса амплитуды U=5мкв, длительности τи=2мкс и
«белого» гауссовского шума со спектральной плотностью мощности N0=10–
18
вт/гц.
Найти и построить:

импульсную характеристику и структуру согласованного фильтра;

сигнал на выходе СФ без шума;

АКФ шума на выходе СФ и его мощность;
112
отношение сигнал/шум на выходе СФ.
Для импульсной характеристики СФ имеем g (t )  k0 S (t0  t ) , где k 0 и t0
постоянные величины, а t0  и .
Структурная схема СФ и АКФ сигнала показаны на рисунке.

Сигнал на выходе СФ без шума совпадает по форме с АКФ входного
сигнала, сдвинутой на время длительности сигнала τи вправо. Для выходного
сигнала имеем:

t  и 
t  и 


 ,
Sвых (t )   S вх (t )g (t  t )dt   k0U 2 и 1 
  k0 E 1 






и
и

где 0  t  2 и – длительность выходного сигнала;
U max  k0 E – амплитуда максимума выходного сигнала.
АКФ шума на выходе СФ может быть найдена как свертка АКФ входного
N
шума R( )  0 ( ) и АКФ импульсной характеристики СФ
2

 

Rg ( )   g (t ) g (t  )dt  k02U 2 и 1   , для  и    и .
 и 

Для АКФ шума на выходе СФ имеем:
 

Rш ( )  2ш 1   ,
 и 
где  и    и ;
k02 EN 0
2
– дисперсия (мощность) шума на выходе СФ;
ш 
и
2
E   S 2 (t )dt  U 2 и – энергия сигнала;
0
k0 – коэффициент передачи интегратора.
Отношение сигнал/шум на выходе СФ по мощности равно
113
q
U max
2и
U
 10.
ш
N0
Пример 5
На вход интегрирующей RC -цепочки с постоянной времени  0
поступает аддитивная смесь прямоугольного видеоимпульса амплитуды U,
длительности τи и белого гауссовского шума со спектральной плотностью
мощности N0= 10– 18вт/гц.
Найти и построить:
 импульсную характеристику цепи;
 АКФ шума и его мощность на выходе цепи;
 отношение сигнал/шум в момент максимума сигнала на выходе цепи;
 рассчитать и построить зависимость коэффициента потерь в

отношении сигнал/шум по сравнению с СФ в зависимости от x  и .
0
Представим прямоугольный импульс на выходе интегрирующей
цепочки в виде:
U (t )  k0 h(t )  h(t  и ) ,
где k 0 – постоянный коэффициент передачи цепи;
 t 
h(t )  1  exp    – переходная характеристика цепи.
 0 
Максимум амплитуды сигнала на выходе цепи наблюдается в момент времени
t   И . Из выражения для выходного сигнала цепи имеем

  
U ( и )  k0U 1  exp   и   .
 0  

Для импульсной характеристики RC - цепи найдем
 t 
dh(t ) k0
 exp    .
g (t ) 
0
dt
 0 
АКФ шума на выходе цепи найдем, как свертку АКФ входного гауссовского
N
белого шума R( )  0 ( ) и АКФ ИХ RC -цепи:
2
114

 
k02
Rg ( )   g (t ) g (t  )dt 
exp   
2
 0 

Для АКФ шума на выходе цепи имеем:
 
N 0 k02
Rш ( )  R( )  Rg ( ) 
exp    .
2 2 0
 0 
Мощность выходного шума равна:
N 0k02
2
.
ш  Rш (0) 
4 0
Отношение сигнал/шум на выходе RC-цепи при воздействии на её вход
прямоугольного импульса найдем как отношение максимума выходного
сигнала U ( и ) к СКО выходного шума:
q( x )  1  exp(  x ) 
4E
,
N0 x

где x  и отношение длительности входного сигнала к постоянной времени
0
цепи;
2E
– отношение сигнал/шум на выходе СФ;
q0 
N0
E  U 2 и – энергия сигнала.
Откуда коэффициент потерь в отношении сигнал/шум равен:
2
( x )  1  exp(  x )  .
x
На рисунке представлен график зависимости потерь в отношении сигнал/шум
(x ) при подаче на вход интегрирующей цепи прямоугольного импульса
длительности  И . Сравнение производится с отношением сигнал/шум на
выходе СФ, равного q 
2E
.
N0
115
Расчеты показывают, что минимум потерь в отношения сигнал/шум на выходе
цепи достигается при x  1,256 , что соответствует и  1,2560 .
2.19.3 Различение сигналов
Пример 6
Определить вероятность ошибки F «идеального наблюдателя» в
когерентном
приемнике, который
обнаруживает
радиоимпульс с
  t 2 
колоколообразной огибающей вида u(t )  U exp      , имеющей
  и  


и =0,1мкс
и
длительность
по
уровню
амплитуду
U = 1мкв
u (  и 2)
 
 exp     0,46 , на фоне теплового шума приёмника, имеющего
U
 4
шумовую температуру T =3000K.
При решении задачи принять, что спектральная плотность мощности
шума равна N 0  kT , где к= 1,38∙10-23 вт/гц – постоянная Больцмана.
Вероятность ошибки различения детерминированного сигнала,
обнаруживаемого на фоне гауссовского шума в приемнике «идеального
наблюдателя» равна
 E 
.
F  1  

2
N
0

Найдем энергию импульса с гауссовской огибающей
116
2

 t  
U 2 и

.
E   U exp  2  dt 



2
 и 


Определим спектральную плотность мощности шума
N 0  kT .
Подставим найденные выражения в формулу для ошибки различения и
получим

и 
 .
F  1   U
2
2
kT


Используя найденное выражение и данные задания, рассчитаем искомое
значение F =0,0018.

2
117
3. РАЗРЕШЕНИЕ СИГНАЛОВ
3.1. Понятие о разрешающей способности сигналов
Разрешение сигналов осуществляется после их обнаружения по ряду
измеряемых полезных параметров. К разрешаемым параметрам сигнала s(t ,  )
можно отнести его временное положение tз , доплеровскую частоту f д ,
направление прихода  с , поляризацию и некоторые другие. Разрешающей
способностью называют способность устройства обработки различать близко
расположенные по указанным параметрам сигналы.
За количественную меру разрешающей способностью на выходе
оптимального приемника (согласованного фильтра) принято принимать
величину минимального отклонения измеряемого параметра  i при которой
нормированные огибающие двух сигналов пересекаются по уровню половины
их максимальных значений.
Разрешающую способность сигналов s(t ,  ) обычно определяют для двух
важных параметров – временной задержки и доплеровской частоты.
3.2 Функция рассогласования сигнала
Под функцией рассогласования сигнала будем понимать времячастотную функцию рассогласования нормированную к единице:


 S (t ) S (t  ) exp( j 2Ft )dt
( , F )   
,

(3.1)
2
 S (t ) dt

где S (t ) – комплексная огибающая сигнала;
, F – рассогласование сигнала по времени и частоте на выходе СФ.
Выражение (3.1) можно представить в спектральной форме. Найдем
спектр комплексной огибающей сигнала

S ( f )   S (t ) exp(  j 2ft )dt ,

как Фурье преобразование от S (t ) . Тогда выражение (3.1) можно представить
в виде
118


 S ( f ) S ( f  F ) exp( j 2ft )df
( , F )   
.

(3.2)
2
 S ( f ) df

Функцию рассогласования ( , F ) , а также 2 ( , F ) , иногда называют телом
неопределенности. Она обладает следующими свойствами.
1)
Свойство центральной симметрии
( , F )  ( , F ) .
2) Свойство единичного объема тела неопределенности
 
V     2 ( , F )ddF  1 .
 
3) Сечение функции неопределенности ( , F ) плоскостью   0
совпадает с нормированным амплитудно-частотным спектром квадрата
2
модуля огибающей S (t ) сигнала:

2

S
(
t
)
exp( j 2 Ft )dt

(0, F )   
(3.3).

2
 S (t ) dt

Выражение (3.3) характеризует значения нормированной огибающей
напряжения на выходе СФ при   0 и различных значениях F – частотного
рассогласования. Функция (0, F ) характеризует разрешающую способность
сигнала по частоте.
4)
Сечение функции неопределенности плоскостью F  0 совпадает с
модулем коэффициента корреляции комплексной огибающей сигнала:


 S (t ) S (t  )dt
( ,0)     
(3.4).
2
 S (t ) dt

Выражение (3.4) характеризует форму модуля нормированной
огибающей на выходе СФ – модуля нормированной АКФ комплексной
огибающей сигнала. Функция (,0) характеризует разрешающую
способность сигнала по задержке (дальности).
119
3.3 Функции рассогласования импульсных сигналов
Найдем функции рассогласования ( , F ) некоторых когерентных
сигналов.
1. Функция рассогласования прямоугольного видеоимпульса. Пусть
необходимо найти функцию рассогласования прямоугольного импульса вида:
1, t  0 2
S0 ( t )  
.
(3.5)
t
0
,


2
0

Подставляя сигнал (3.5) в выражение (3.1) получим
 sin F0 1   0 

F0 ,   0 .
(3.6)
0 ( , F )  

для   0
 0,
На рис. 3.1 показана функция рассогласования комплексной огибающей
прямоугольного импульса.
Рис 3.1
Сечение функции рассогласования плоскостью F  0 дает АКФ
прямоугольного импульса (,0) . На рис. 3.2 показана АКФ прямоугольного
импульса.
120
Рис. 3.2
Из выражения (3.6) и рис. 3.2 видно, что разрешающая способность по
времени равна t  0 .
Сечение функции рассогласования плоскостью   0 дает модульное
значение спектра импульса (0, F ) (амплитудный спектр), показанное на рис.
3.3.
Рис.12.3
Из представленного на рис. 3.3 графика видно, что разрешающая способность
1
по частоте равна f  .
0
121
2. Функция рассогласования из N прямоугольных импульсов. Найдем
комплексную огибающую функции рассогласования пачки из N импульсов,
заданных выражением:
N
2
S N (t )   S0 (t  iT0 ) ,
(3.7)
N
i 
2
где T0 – период следования прямоугольных импульсов.
Подставляя (3.7) в выражение (3.1), и производя вычисления, получим:
1 N 1 sin( N  i ) FT0 
( , F ) 
0 (   iT0 , F ) exp(  jiFT0 ) ,

N i  ( N 1)
sin FT0
(3.8)
где 0 ( , F ) – функция рассогласования прямоугольного импульса (3.6). На
рис. 3.4 показана функция рассогласования комплексной огибающей пачки из
N  5 импульсов со скважностью два.
Рис. 3.4
Сечение функции рассогласования плоскостью F  0 дает нормированную
АКФ пачки из N прямоугольных импульсов (,0) . На рис. 3.5 показана
нормированная АКФ пачки из N  5 прямоугольных импульсов.
Рис. 3.5
Из представленной зависимости следует, что разрешающая способность по
времени является периодической функцией с периодом равным периоду
122
повторения импульсов T0 . Этот интервал определяет период однозначного
разрешения по времени (дальности) t Р   0 .
Сечение функции рассогласования плоскостью   0 дает нормированное
по амплитуде значение спектра квадрата комплексной огибающей пачки из N
прямоугольных импульсов (0, F ) , показанное на рис. 3.6.
Рис. 3.6
Из представленной зависимости следует, что разрешающая способность по
частоте является периодической функцией с периодом равным F0  1 T0 . Этот
интервал определяет период однозначного разрешения по частоте f Р  1 NT0 .
Из представленных зависимостей видно, что чем больше интервал
однозначного разрешения по времени, тем меньше интервал однозначного
разрешения по частоте и наоборот.
3.
Линейно-частотно-модулированный
(ЛЧМ)
сигнал
с
прямоугольной огибающей называется импульс с линейным изменением
частоты в пределах его длительности по линейному закону. Мгновенная
частота такого сигнала может линейно нарастать в пределах импульса
T
T
f
(3.9)
t, при   t  ,
f (t )  f 0 
2
2
T
где f 0 – средняя частота импульса;
f – девиация частоты;
T – длительность сигнала.
С учетом (3.9) ЛЧМ сигнал с прямоугольной огибающей имеет вид
123

2
cos(
2



),
f
t
t
0

s (t )  
 0,

T
2,
T
t 
2
t 
(3.10)
 f D
 2 – величина пропорциональная скорости изменения частоты
T
T
сигнала, а D  fT – база ЛЧМ сигнала. На рисунке 3.5 показан ЛЧМ сигнал с
нарастающим во времени законом изменения частоты и прямоугольной
огибающей.
где  
Рис. 3.5
Комплексная огибающая ЛЧМ сигнала с прямоугольной огибающей
имеет вид
T

2
exp(

),

j
t
t

2
S (t )  
(3.11)
T
 0,
t 

2
Для импульса с колоколообразной огибающей комплексная амплитуда ЛЧМ
сигнала имеет вид
2
exp( jt 2 ) .
S (t )  exp    t
(3.12)
T 

Частотные спектры комплексных амплитуд ЛЧМ сигналов являются
Фурье-преобразованием от их комплексных амплитуд
 

S ( f )   S (t ) exp( 2ft )dt  S ( f ) exp j( f ),
(3.13)

где S ( f ) – амплитудно-частотный, а ( f ) – фазо-частотный спектры.
Амплитудно-частотный спектр комплексной огибающей колокольного ЛЧМ
импульса имеет вид
124
S ( f ) 
T


exp  f 2 f 2 .
(3.14)
1 D
При D  fT  1 ЛЧМ импульс имеет близкую к девиации частоты f
ширину спектра по уровню 0,46 от максимального значения
2
1  D2
(3.15)
f и 
 f .
T
Фазо-частотный спектр сигнала имеет уравнение убывающей параболы
2
 f  1
( f )  D   arctgD .
(3.16)
2
 f 
Амплитудно-частотный спектр комплексной огибающей прямоугольного
импульса выражается через интегралы Френеля. При больших базах
D  fT  1 амплитудный спектр можно представить в следующем виде
 T
f
f 
 4f ,
2 .
S ( f )  
(3.17)

f
0,
f 

2
Фазо-частотный спектр ЛЧМ импульса имеет квадратичную зависимость
от частоты, в пределах действия сигнала и может быть приближенно
представлен выражением (3.16).
Нормированная функция рассогласования прямоугольного ЛЧМ
импульса может быть представлена в виде
 T2  
 1 exp j 2(   F x  jx 2 )dx , для - T    0
 T T

2
.
( , F )  
T
1 2
exp j 2(   F x  jx 2 )dx , для 0    T


 T  T2  
(3.18)
Проводя операцию интегрирования выражения (3.18) получим

  D
 

 FT 1  
 sin  
 T  
  T

( , F )  
,

 D

 FT 


 T

 T
0,
125
 T .
(3.19 )
Рассмотрим функцию рассогласования сигнала с прямоугольной
огибающей и линейно нарастающей во времени частой, показанной на рис.
(3.6). Она рассчитанная с использованием выражения (3.18) для сигнала
T  100 и девиации частоты f  1 .
Рис. 3.6
Из представленной на рисунке поверхности нормированной функции
рассогласования ЛЧМ сигнала видно, что в отличие от прямоугольного
импульса поверхность имеет узкий вытянутый гребень по диагонали с
отрицательным углом наклона на время-частотной плоскости. Заметим, что
для ЛЧМ сигнала с убывающим во времени законом изменения частоты угол
наклона будет положительный.
F 0
дает
Сечение
функции
рассогласования
плоскостью
нормированную АКФ ЛЧМ импульса (,0) , показанную на рис.3.7.
126
Рис.3.7
Из представленной зависимости следует, что разрешающая способность по
времени ЛЧМ сигнала равна tР 
1
.
f
Сечение функции рассогласования плоскостью   0 дает нормированное
по амплитуде значение квадрата спектра комплексной огибающей ЛЧМ
импульса (0, F ) , показанное на рис. 3.8.
Рис.3.8
Из представленных данных видно, что разрешающая способность по частоте
ЛЧМ сигнала обратно пропорциональна его длительности f Р 
1
.
T
Для ЛЧМ сигнала с гаусовской огибающей функция рассогласования
имеет вид
   1  D 2  2

( , F )  exp  
 2 DF   2 F 2  .
2
T

 2
Для D  0 она совпадает с функцией рассогласования радиосигнала с
комплексной огибающей по гаусовскому закону (3.12).
Из представленных данных для ЛЧМ сигнала видно, что длительность
нормированного по амплитуде сигнала на выходе СФ уменьшилась
127
1 T

в D раз. Произошло сжатие выходного сигнала, что увеличивает
f D
разрешающую способность по времени в D раз.
tР 
3.4 Основы статистической теории измерения
параметров радиолокационных сигналов
Измерение (оценивание) параметров радиолокационных сигналов –
важнейшая составная часть получения информации в РТС. В
радиолокационных системах измерению подлежат компоненты  i вектора
(1,...,  n ) . В качестве измеряемых параметров часто выступают: время
задержки эхо сигнала tз доплеровское смещение частоты зондирующего
сигнала Fд , пространственные координаты (азимут и угол места цели).
Измерение параметров может осуществляться как после достоверного
обнаружения сигнала, так и совместно с её обнаружением в устройстве,
называемом обнаружитель-измеритель.
В результате измерения на выходе устройства получается так называемая
точечная оценка измеряемого параметра ̂ i отличная от истинного значения
 i в результате действия помех:
u(t )  s(t, ˆ )  n(t ) .
В качестве оценки точности измерения параметра может быть указан
доверительный интервал, в пределах которого измеряемый параметр лежит с
заданной доверительной вероятностью.
i
может представлять собой, как
Измеряемый параметр
детерминированную, так и случайную величину. Для его оценки в последнем
случае необходимо знать его априорное распределение W ( i ) . При наличии
данных предыдущих измерений (циклов обзора) измеряемые параметры
можно считать случайными величинами и уточнять их значения в процессе
измерения.
Если измеряемый параметр медленно меняется во времени, то задача
оценки параметра переходит в задачу фильтрации параметра и синтеза
оптимального устройства слежения за измеряемой величиной.
Пусть ошибка измеряемого параметра не имеет систематической
составляющей (математического ожидания), а имеет флюктуационную
компоненту   i  ˆ i с известным законом распределения W () . В качестве
характеристик оценки измеряемого параметра  i могут служить:
математическое ожидание, дисперсия, среднеквадратическое отклонение,
медианное значение, доверительный интервал.
128
Обобщенным показателем качества оцениваемого параметра может
являться усреднённое по всем значениям ̂ i и возможным результатам
наблюдения u(t ) средний риск R с учетом функции потерь:
R
П(  , ˆ ( u))W (  , u)d  du
(3.20)

U
где W ( , u) – совместная плотность вероятности распределения оцениваемых
параметров    и наблюдаемой реализации u  U , где П( , ˆ (u)) – функция
потерь. На практике широкое распространение получили функции потерь
П  П ( ) , зависящие только от ошибки оценивания   i  ˆ i . Для скалярного
параметра  практическое распространение получили квадратичная, линейная
и релейная функции потерь. Оптимальная система измерения параметров
должна обеспечивать для заданной функции потерь Rmin минимум среднего
риска в выражении (3.20).
3.5 Оптимальный алгоритм измерения параметров
Пусть на входе приемного устройства, на интервале t  [0, T ] наблюдается
аддитивная смесь сигнала и шума
(3.21)
u(t )  s(t,  )  n(t ) ,
где (1,...,  n ) вектор детерминированных и случайных параметров
принимаемого сигнала. В результате обработки принимаемого колебания
необходимо синтезировать устройство получения максимально точных оценок
измеряемых параметров сигнала ̂ i в пространстве оцениваемых параметров
сигнала    и пространстве вектора наблюдаемой реализации u  U .
Наличие шума n(t ) и случайных параметров (1,...,  n ) приводит к тому, что
задача носит статистический характер. Решение задачи сводится в отыскании
оптимального алгоритма работы измерителя параметров сигнала путем
минимизации среднего риска выражения (3.20) при заданной функции потерь.
Для квадратичной функции потерь и скалярного параметра имеем
Rкв    ( - ˆ (u))2W (, u)ddu .
(3.22)
U
Совместную плотность вероятности W (, u) можно представить в
следующем виде
(3.23)
W (, u)  W (u)W ( / u) ,
где W (u) – априорная плотность распределения выборочных значений
наблюдаемого входного процесса;
129
W ( / u) – апостериорная плотность вероятности распределения случайного
параметра в принятой реализации. Плотность вероятности W ( / u) несет всю
послеопытную информацию об измеряемом параметре λ.
Подставляя выражения (13.23) в (13.22) имеем
Rкв    ( - ˆ (u))2W ( / u)W (u)ddu .
(3.24)
U
В выражении (3.24) интегрируемые функции положительно
определенные, поэтому минимум выражения определяется производной от
квадратичного множителя подынтегрального выражения. Для оцениваемого
параметра имеем
(3.25)
ˆ кв   W ( / u)d .

Из выражения (3.25) следует, что оптимальное значение измеряемого
параметра при квадратичной функции потерь является среднее значение
апостериорной плотности вероятности оцениваемого параметра.
Можно показать, что для линейной функции потерь минимальная
ошибка измерения оцениваемого параметра равна
ˆ лин  ˆ м .
где  м медианное значение параметра функции распределения W ( / u) .
Для релейной функции потерь минимизация среднего риска в выражении
(3.20) дает значение ̂ р из условия отыскания максимального значения
функции правдоподобия W ( / u)max  . Для ряда практических задач при
гладкой апостериорной функции распределения максимальное значение
удобно найти, как производную от логарифма этой функции
d ln W ( / u)
(3.26)
 0.
d
ˆ
 
В соответствии с формулой Байеса имеем
W (u /  )W ( )
.
(3.27)
W ( / u) 
W ( u)
Подставляя (3.27) в (3.26), и проводя элементарные преобразования, получим
d ln W ( / u)
d ln W (u / )
d ln W ( )
 0 , (3.28)


d
d
d


ˆ
ˆ
ˆ
 
 
 
где W ( ) – априорная плотность вероятности распределения измеряемого
параметра  ;
W (u / ) – функция правдоподобия.
130
Из (3.28) видно, что оптимальное значение оцениваемого параметра
находится как максимальное значение функции правдоподобия с учетом
максимума априорного распределения случайного параметра  .
В случае отсутствия априорных данных о распределении измеряемого
параметра (равномерное распределение параметра в пределах заданных
значений) выражение для оптимального алгоритма оценки параметра имеет
вид
d ln W ( / u)
d ln W (u / )
(3.29)
 0.

d
d

ˆ
ˆ
 
 
Из (3.29) следует, что оптимальное значение параметра будет
определяться максимумом функции правдоподобия. Выражение (3.28)
называется уравнением максимальной апостериорной вероятности. Методы
получения максимального значения оцениваемого параметра и дает алгоритм
работы оптимального измерителя параметров сигналов.
3.6 Измерение параметров радиолокационных сигналов
Проведенный ранее анализ показывает, что процедура измерения
параметров радиолокационных сигналов заключается в том, что по принятой
реализации необходимо сформировать функцию, пропорциональную
апостериорной плотности вероятности (3.27), или монотонную функцию от
неё в заданном диапазоне измерения параметров. Из (13.27) следует что
W (u /  )W ()
 l ( )W ( ) ,
W ( u)
где l ( ) – отношение правдоподобия. Возьмем монотонную функцию
логарифма от последнего выражения и получим
(3.30)
lnW ( / u)  ln l ()  lnW () ,
Из (3.30) следует, что оптимальный измеритель радиолокационных
сигналов по принятой реализации должен формировать функцию
пропорциональную логарифму отношения правдоподобия. Эту операцию
выполняет оптимальный обнаружитель радиолокационного сигнала. Можно
показать, что для сигнала со случайной начальной фазой логарифм отношение
правдоподобия имеет вид
ln l ( )  Z ( )  q 2 2 ,
(3.31)
а для сигнала со случайной амплитудой и начальной фазой
Z 2 ( )
q2
 ln(1  ) .
ln l ( ) 
(3.32)
2
2
4(1  q 2)
W (  / u) 
131
В выражениях (3.31) и (3.32) Z ( ) модульное значение комплексного
корреляционного интеграла
1 T
Z ( ) 
u(t ) s (t , )dt ,

N0 0
(3.33)
где N 0 – спектральная плотность мощности белого гауссовского шума;
q 2  2 E N 0 – параметр обнаружения.
Анализ показывает, что оптимальный измеритель радиолокационного
сигнала на фоне белого гауссовского шума должен вычислять
корреляционный интеграл (либо его квадрат) в заданном диапазоне
ожидаемых значений измеряемого параметра. Вместо корреляционного
приемника эту операцию может выполнять согласованный фильтр и
устройство отбора максимального значения.
Исходя из алгоритма работы оптимального устройства измерения
параметров сигнала, измерители можно разделить на следящие и неследящие.
Не следящие формируют сигнал, пропорциональный апостериорной
плотности вероятности распределения во всём диапазоне возможных значений
изменения параметров. В рассматриваемом случае отсутствует априорная
плотность распределения измеряемого параметра.
В следящих измерителях присутствуют априорные сведения о параметре
и эти данные уточняются по мере накопления данных.
3.6.1 Неследящие измерители дальности
Пусть необходимо измерить дальность до цели rц и получить её
оптимальную оценку r̂ц . Оценку дальности будем получать путем измерения
времени запаздывания эхо-сигнала относительно зондирующего
cˆ
rˆц  з .
2
Для этого необходимо сформировать статистику Z () или Z 2 ( ) для
всей области изменения параметра  min  ˆ з   max . За оптимальную оценку
измеряемого параметра ̂ з согласно алгоритму оптимального измерения
параметра необходимо принять максимальное значение корреляционного
интеграла. Вычисление корреляционного интеграла возможно провести
корреляционным, фильтровым и корреляционно-фильтровым методами.
Устройство обработки фильтровым методом показано на рис. 3.9.
132
Рис.3.9
Устройство состоит из согласованного фильтра (СФ), детектора
огибающей (ДЕТ) и решающего устройства (РУ). В решающем устройстве в
момент достижения модульного значения выходной функции Z ()
максимального значения производится измерение времени запаздывания
сигнала относительно момента его излучения. В результате действия помехи
это значение отличается от истинного значения времени запаздывания на
величину ошибки измерения   з  ̂з .
Временное запаздывание эхо-сигнала может быть проведено
корреляционным или корреляционно-фильтровым методом. Структурная
схема корреляционной обработки представлена на рис.3.10.
Рис.3.10
Она состоит из многоканальной системы корреляционных приёмников,
настроенных на временные задержки эхо-сигналов в пределах ожидаемых
интервалов запаздывания сигналов  з1  ˆ з   зN и детектора огибающей
сигнала. В решающем устройстве (РУ) производится отбор максимального
выходного сигнала i-го корреляционного приемника с временным
запаздыванием  зi .
3.6.2. Неследящие измерители скорости
Радиальную составляющую скорости цели V R измеряют по результатам
выделения доплеровского смещения частоты Fд отраженного от цели сигнала
2V
Fд  R , где λ0 длина волны несущего колебания. Для получения оценки F̂д
0
оптимальный измеритель скорости вычисляет модуль комплексного
корреляционного интеграла Z ( Fдi ) для СФ i-го канала обработки при
133
фильтровом методе. Соответствующее значение доплеровского канала в
решающем устройстве поступает на выход схемы обработки, показанном на
рис. 3.11.
Рис.3.11
Схема измерения скорости представляет собой многоканальное
устройство обработки с СФ, настроенными на зондирующий сигнал с
доплеровским сдвигом Fд1  Fˆд  FдN и детектора огибающей. В решающем
устройстве выбирается сигнал с максимальным выходным амплитудным
значением и соответствующий ему доплеровский сдвиг по частоте.
Заметим, что данное устройство при наличии достаточного количества
каналов обработки воспроизводит (при отсутствии или незначительном уровне
шумов) функцию неопределенности зондирующего сигнала. Такая схема
обработки, следовательно, позволяет при наличии «кнопочной» функции
неопределенности зондирующего сигнала производить совместное измерение
дальности и скорости цели.
3.7 Следящие измерители параметров цели
В процессе работы РЛС производится последовательное выполнение
операций обнаружения, измерения параметров цели (дальности и скорости) и
слежение за измеряемыми параметрами во времени. Слежение за
измеряемыми параметрами цели является задачей вторичной обработки
радиолокационных данных. В качестве устройств измерения параметров цели
могут применяться следящие измерители дальности и скорости. Обобщенная
схема следящего измерителя представлена на рис. 3.12.
134
Рис.3.12
На вход устройства слежения поступает измеряемый параметр  (t ) ,
выделенный из принимаемого эхо-сигнала. В качестве устройства ( Д ИС)
используется либо временной для слежения за изменением дальности цели,
либо частотный для слежения за доплеровским сдвигом частоты
дискриминатор. На второй вход дискриминатора поступает оценка параметра
слежения, полученная ранее. На выходе дискриминатора вырабатывается
сигнал рассогласования     ˆ
измеряемого параметра. Сигнал
рассогласования подвергается сглаживанию, в результате чего на выходе
фильтра нижних частот (ФНЧ) формируется управляющее напряжение uр (t ) ,
изменяющее значение оцениваемого параметра на выходе регулятора (РЕГ) ̂
в зависимости от знака и величины сигнала рассогласования.
Ранее было показано, что логарифм отношения правдоподобия с
точностью до постоянной величины совпадает с модульным значением
корреляционного интеграла Z (t, ) либо с его квадратом (см. выражение (3.31)
и (3.32)). Для нахождения алгоритма работы устройства слежения разложим
Z (t ,  ) в ряд Тейлора по параметру измерения ̂
(  ˆ )2
ˆ
ˆ
ˆ
ˆ
(3.34)
Z ()  Z ()  Z ()(  )  Z ( )
 ...
2
Оптимальная оценка измеряемого параметра находится в точке максимума
корреляционного интеграла, где первая производная обращается в нуль.
Продифференцируем (3.34) по параметру  и получим
Z ()  Z (ˆ )  Z (ˆ )(  ˆ )  0 .
Из последнего выражения следует, что малое отклонение измеряемого
параметра     ˆ от истинного значения может быть получено в виде
Z (ˆ )
.
(3.35)
  
Z (ˆ )
Выражение (3.35) задает алгоритм работы дискриминатора системы слежения
за параметром цели.
3.8 Точность измерения радиолокационных параметров
Найдем потенциальную (максимально возможную) точность измерения
информационных параметров радиолокационного сигнала. Считаем, что
измерение выполняется при высоком отношении сигнал/шум (порядка 8-10),
т.е. является регулярным. Предполагаем, так же, что функция правдоподобия
W (u / ) гладкая, унимодальная и дважды дифференцируемая. Допустим, что
135
ошибка измерения параметра     ˆ (u) имеет гауссовское распределение с
нулевым математическим ожиданием. Тогда разброс (точность) измерения
одиночного информационного параметра будет определяться дисперсией
ошибки, либо СКО
2 (  ˆ (u))  M (  ˆ (u)) 2 .
При совместной оценке нескольких параметров, разброс будет зависеть от
корреляционной (ковариационной) матрицы ошибок с элементами Rij  i  j .
Нижняя (минимальная)
неравенству Крамера-Рао:


граница
матрицы
ошибок
подчиняется




1


2
ˆ
 ( λ  λ ( u))   M  2
(3.36)
.
 d ln W ( u / λ ) 


dλ 2
Для оценки нижней границы разброса параметров строится обратная величина
в многомерном случае матрица точности (матрица Фишера) с элементами
  2 lnW ( u / λ ) 
Cij   M 
(3.37)
,






i
j
где i, j  [1, m] , а m – размерность вектора параметров  (1 ,...,  m ) ;
 c11 ... c1m 


C   ... ...
...  – матрица точности (матрица Фишера).
c

 m1 ... cm m 
Матрица точности связана с корреляционной матрицей соотношением
R  C 1 .
При определении границ ошибок измерения случайных параметров
матрица точности учитывает информацию об априорном распределении
параметра
C  C A  C ,
где C A – матрица точности априорных ошибок измерения случайных
параметров;
  2 ln W ( λ ) 
A
Cij   M 
 – элементы матрицы точности априорных ошибок





i
j 

измерения. Нижняя граница ошибок измерения случайных параметров связана
с матрицей точности соотношением R   C1 . Диагональные элементы
136
матрицы R  определяют дисперсию нижней границы оценки разброса
соответствующих случайных параметров  i .
3.8 Потенциальная точность измерения
радиолокационных параметров
3.8.1. Точности измерения временного запаздывания
В соответствии с выражением (3.31) и (3.32) оценка временного
запаздывания tз производится на выходе СФ по максимуму модульного
значения корреляционного интеграла Z ( , F ) . Выражение можно представить
через функцию рассогласования ( , F ) в виде
(3.38)
Z ( , F )  q( , F ) ,
2E
– отношение сигнал/шум. Из выражения (3.37) с учетом того, что
N0
частота и отношение сигнал/шум являются параметрами, имеем
1
,
(3.39)
 
 (0,0)
q 
где q 
 (0,0) 
где 
 2(0, )
 2
.
0
 (0,0)
имеет размерность частоты
Величина

эффективную ширину спектра зондирующего импульса:

и
характеризует
спектр
зондирующего
2
2
 S ( f ) f df
f эф  2


,
2
 S ( f ) df

где

S ( f )   s(t ) exp(  j 2ft )dt
–
комплексный

импульса.
Подставляя эффективную ширину спектра сигнала в выражение (3.39)
окончательно получим
1
 
.
(3.40)
qf эф
137
Из (3.40) видно, что ошибка измерения временного запаздывания сигнала
уменьшается с ростом ширины спектра импульса и отношения сигнал/шум.
3.8.2. Точность измерения частоты
Используем ранее полученное выражение для СКО измеряемого
параметра  в зависимости от отношения сигнал/шум и функции
рассогласования. В выражении (3.39) заменим вторую производную по
времени на производную по частоте
1
,
(3.41)
F 


q  FF (0,0)
где
 (0,0) 
FF
 2(0, F )
F 2
–
характеризует
ширину
пика
функции
F 0
рассогласования по частоте, имеет размерность квадрата времени. Величину
 (0,0) можно интерпретировать, как эффективную длительность
FF
зондирующего импульса

2
 t S (t ) dt
 эф  2


2
.
(3.42)
2
 S (t ) dt

С учетом полученного выражения (3.42) для СКО измерения частотного
сдвига зондирующего импульса можно получить
1
.
(3.43)
F 
q эф
Из выражения (3.43) следует, что точность измерения частоты растет с ростом
эффективной длительности зондирующего импульса и отношения сигнал/шум.
3.8.3. Точность измерения угловой координаты
Пусть имеется антенна с размером апертуры величины LА , с
распределением напряженности электрического поля возбуждения вдоль
антенны E (x ) и длиной волны  0 . Для такой антенны можно найти
нормированную функцию рассогласования на угол  от направления на
максимум диаграммы направленности  max как Фурье-преобразование от
распределения амплитуды поля возбуждения вдоль антенны вида
138
 L

sin  A (sin max  sin 
 0
.
( , max ) 
LA
(sin max  sin )
0
Функция рассогласования по пространственной координате ( ,  max )
определяет точность пространственного положения цели. Используя ранее
полученные выражения (3.39) и (3.41), аналогично для среднеквадратической
ошибки измерения углового положения цели получим
1
,
 
 (max , )
q 
   max
где
 (  max , )   

max

 2(  max , )

2
– величина, совпадающая с
   max
квадратом эффективной ширины диаграммы направленности антенны

эф  0
2Lэф . Величина эффективной длины апертуры антенны может быть
найдена через E (x ) – функцию распределения напряженности электрического
поля вдоль апертуры антенны

2
 x E ( x ) dx
Lэф 
2


.
2
 E ( x ) dx

Подставляя найденные выражения в формулу для СКО измерения угловой
координаты, имеем
эф
0
.
 

2 qLэф
q
Из полученного выражения видно, что с ростом длины апертуры антенны и
отношения сигнал/шум растет и точность определения угловой координаты.
3.8.4. Точность совместного измерения
времени запаздывания и частоты
При совместном измерении времени запаздывания с ошибкой   tз  tˆз
и частоты с ошибкой  F  FД  F̂Д вектор-столбец ошибок представим в виде
139
  
  . Предполагаем, что компоненты вектора имеют нормальное
 F 
распределение с нулевым математическим ожиданием. Матрица точности
(матрица Фишера) совместного измерения времени запаздывания и частоты
(3.37) имеет вид


 2

 2
  M   ln l ( , F )   M   ln l ( , F )  

 F  


2
C
,
2
2




  M   ln l ( , F )   M   ln l ( , F )  




2

F




 


F





где ln l ( , F ) – логарифм отношения правдоподобия (3.31), (3.38). Обратная ей
корреляционная матрица ошибок измерения R  C1 имеет вид
  r 2 
,
R   2


r

F
1
– СКО ошибки измерения дальности цели;
q  (0,0) (1  r 2 )
1
– СКО ошибки измерения частоты цели;
F 
 (0,0) (1  r 2 )
q FF
где  
F (0,0)
– квадрат коэффициента взаимной корреляции связи между
r 
 (0,0) (0,0)
FF
измерениями по временному запаздыванию и частотному сдвигу. При r  0
2
2
точность измерений временного запаздывания и частотного сдвига снижается.
Если r  0 – точность измерений максимальная и функция рассогласования
сигнала симметрична в плоскостях сечения   0 и F  0 .
Можно показать, что для простых сигналов, ФКМ сигналов и
когерентных пачек импульсных сигналов коэффициент r  0 . Например, для
простого импульсного сигнала с гауссовской огибающей
  t 2 
s(t )  exp    
  и  
нормированная функция рассогласования имеет вид
     2


2 
( , F )  exp     ( и F )  
 
 2  и 

и отражает отсутствие корреляционной связи между  и F , поскольку
 (0,0)  0 . Корреляционная матрица ошибок измерения имеет вид
F
140

R   
0
где  
0 
,
 F 
2
и
и F 
– СКО определения дальности и частотного
q и 
q 
сдвига.
Для сигналов с частотной модуляцией коэффициент взаимной
корреляции r  0 , что приводит к снижению точности измерения временного
запаздывания и частотного сдвига. Для примера проведем расчет
корреляционной матрицы ошибок измерения по  и F для ЛЧМ сигнала с
гауссовской огибающей
2
 jt 2  ,
s(t )  exp    t
T


 
где T – длительность гауссовского ЛЧМ сигнала по уровню exp     0,46
 4
D
от максимального амплитудного значения, а   2 – скорость изменения
T
 
1  D2
частоты ЛЧМ сигнала, D  fT – база ЛЧМ сигнала, а f 
–
T
девиация частоты ЛЧМ сигнала по уровню 0,46 от максимального значения
амплитудного спектра ЛЧМ импульса
 f 2 
T

S( f ) 
exp  2  .
2
1 D
 f 
Нормированная функция рассогласования такого сигнала имеет вид
   1  D2 2

2 2 
( , F )  exp  




D
F
T
F
2
.
 T2

2



Ковариационная матрица ошибок измерения имеет вид
  r 2 
,
D   2
 F 
r
1
T
где  
и F 
– СКО определения дальности и частотного
qD 
qT 
сдвига. Величина r 
4D2
 4 отлична от нуля, что говорит о жёсткой
1  D2
зависимости сдвига по частоте F и временного положения сжатого импульса
 . Можно показать, что частотный сдвиг на величину F приводит к
2
141
возникновению пропорционального ему измерению временного положения
T
импульса на время   
F относительно максимального положения
f
функции рассогласования.
3.9
Примеры
3.9.1 Функция рассогласования сигнала
Пример 1
На вход радиолокационного приемного устройства поступает
когерентная пачка с прямоугольной огибающей из M прямоугольных
радиоимпульсов длительности  и и частотой повторения T с частотой
заполнения f0 =300Мгц, Найти и построить сечения функции рассогласования
сигнала ρ(τ,F).
Определить потенциальную разрешающую способность РЛС по
дальности, скорости; определить максимальные значения однозначного
определения дальности и скорости. Данные для расчета: M=10, τи=1мкс,
T=3мс.
Функция рассогласования прямоугольной пачки из M прямоугольных
импульсов имеет вид:
M 1
sin( ( M  m ) FT
( , F ) 
0 (   mT , F ) exp(  jmFT ) ,

M
FT
sin(
)

m   ( M 1)
где 0 
sin( Fи (1 
Fи

и
))
–
функция рассогласования одиночного
прямоугольного видеоимпульса для   и .
Для получения разрешающей способности по времени (дальности)
необходимо найти и построить сечение функции рассогласования по частоте,
которая совпадает с модулем коэффициента корреляции комплексной
огибающей сигнала. Из функции рассогласования для пачки импульсов для
F=0 имеем:
M 1
  mT
),
( ,0) 
 (1 

и
m  ( M 1)
для  и  mT    и  mT и целого m в пределах  ( M  1)  m  ( M  1) . На
рисунке показана АКФ огибающей для пачки из M=5 импульсов.
142
Из рисунка видно, что разрешающая способность по времени для такого
сигнала равна τи, а временной интервал однозначного определения задержки
равен T. Связывая время задержки и дальность через скорость
распространения ЭМВ C  3  108 м/с, найдем разрешающую способность по
дальности и однозначно определяемую дальность. Разрешающая способность
С
по дальности имеет вид r  и , а максимальная дальность однозначного
2
СT
определения равна Dmax 
.
2
Для получения разрешающей способности по частоте (скорости)
необходимо найти и построить сечение функции рассогласования по времени,
которая совпадает с нормированным амплитудно-частотным спектром
2
квадрата модуля огибающей S (t ) сигнала.
Из выражения для функции рассогласования при  =0 имеем:
M 1  sin( ( M  m ) FT  sin( F )
и exp(  jmFT ) .
(0, F ) 
 

M sin( FT )  Fи
m   ( M 1) 
На рисунке представлен
рассогласования по времени.
график
143
зависимости
сечение
функции
Из графика зависимости можно найти разрешающую способность по
частоте равную f  1
и максимальный однозначно определяемый сдвиг
MT
1
по частоте равный F  . Частотный сдвиг зондирующего импульса по
T
частоте связан с наличием радиальной составляющей скорости цели на
направление на РЛС. Найдем разрешающую способность по скорости
C
C
Vр 
f 
и максимальную величину однозначно определяемой
2 f0
2 f 0 MT
C
C
F 
скорости Vmax 
. Подставляя данные условия задачи в
2 f0
2 f 0T
приведенные ранее выражения, можно получить следующие данные: ∆r=150м,
Dmax=450км, ∆Vр=1,7 м/с, Vmax=16,6 м/с.
3.9.2. Потенциальная точность определения
дальности и скорости цели
Пример 2
Зондирующий радиоимпульс РЛС имеет гауссовскую форму
  t 2


u(t )  U exp     j 2f 0t  с параметрами τи и f0. Для некоторой цели
  и 



144
вероятности правильного обнаружения и ложной тревоги равны,
соответственно D=0,9 и F=10-4.
Определить потенциальные точности измерения дальности  r до этой
цели и её радиальной скорости V . Данные для решения задачи: f0 =1Ггц,
τи=10мкс, D=0,9, F =10-4.
Для простого импульсного сигнала с гауссовской комплексной
  t 2 
огибающей вида U (t )  U exp      функция рассогласования имеет вид:
  и  


     2


2 
( , F )  exp     ( и F )   .
 
 2  и 

Потенциальная точность определения запаздывания равна:
1
,
 
 (0,0)
q 
где q – отношение сигнал/шум;

f эф 
 (0,0)  2

2
2
 F G ( F ) dF


– эффективная ширина спектра;
2
 G ( F ) dF

G(F ) – спектр комплексной огибающей.
Для импульса гауссовской формы потенциальная точность определения
временного запаздывания имеет вид:

  и .
q 
Аналогично потенциальная точность определения частотного сдвига равна:
1
,
F 
 (0,0)
q FF

где
 эф 
 (0,0)  2
FF
2
2
 t U (t ) dt


–
эффективная
2
 G (t ) dt

гауссовского импульса U (t ) . Для гауссовского импульса имеем:
145
длительность
F 
2
q и 
.
Разрешающая способность по дальности имеет вид r 
Си
, откуда
2
С
Си
.
 
2
2q 
Аналогично связывая сдвиг по частоте с доплеровским смещением сигнала
при наличии радиальной составляющей скорости цели, можно найти
C
f , откуда
разрешающую способность по скорости Vр 
2 f0
С
C
V 
F 
.
2 f0
qи f 0 
По характеристикам обнаружения для заданных вероятностей правильного
обнаружения D=0,9 и ложной тревоги F=10-4 найдем пороговые отношения
сигнал/шум q =5.
Используя полученные выражения и исходные данные можно получить
искомые точности определения дальности  r =173м и скорости V =3,4 км/с.
r 
146
ПРИЛОЖЕНИЕ
Нормированная функция Лапласа
Функцию распределения гауссовского типа в конечных пределах обычно
находят через таблицы интегральной функции Лапласа.
U
1
 exp
2π 0
(U ) 
U
0
1
2

t2
2 dt  1 erf  U  .
3
2
 2
Таблица П.1
4
5
6
7
8
9
0,0 0,0000
00399 00798 01197 01595 01994 02892 02790 03188 03586
0,1 0,03983
04380 04776 05172 05567 05962 06356 06749 07142 07535
0,2 0,07926
08317 08706 09095 09483 09871 10257 10642 11026 11409
0,3 0,11791
12172 12552 12930 13307 13683 14058 14431 14803 15173
0,4 0,15542
15910 16276 16640 17003 17364 17724 18082 18439 18793
0,5 0,19146
19497 19847 20194 20540 20884 21226 21566 21904 22240
0,6 0,22575
22907 23237 23565 23891 24215 24537 24857 25175 25490
0,7 0,25804
26115 26424 26730 27035 27337 27637 27935 28230 28524
0,8 0,28814
29103 29389 29673 29955 30234 30511 30785 31057 31327
0,9 0,31594
31859 32121 32381 32639 32894 33147 33398 33646 33891
1,0 0,34134
34375 34614 34850 35083 35314 35543 35769 35993 36214
1,1 0,36433
36650 36864 37076 37286 37493 37698 37900 38100 38298
1,2 0,38493
38686 38877 39065 39251 89435 39617 39796 39973 40147
1,3 0,40320
40490 40658 40824 40988 41149 41308 41466 41621 41774
1,4 0,41924
42073 42220 42364 42507 42647 42786 42922 43056 43189
1,5 0,43319
43448 43574 43699 43822 43943 44062 44179 44295 44408
1,6 0,44520
44630 44738 44845 44950 45053 45154 45254 45352 45449
1,7 0,45543
45637 45728 45818 45907 45994 46080 46164 46246 46327
1,8 0,46407
46485 46562 46638 46712 46784 46856 46926 46995 47062
1,9 0,47128
47193 47257 47320 47381 47441 47500 47558 47615 47670
2,0 0,47725
47778 47831 47882 47932 47982 48030 48077 48124 48169
1
0,48214
48257 48300 48341 48382 48422 48461 48500 48537 48574
2
0,48610
48645 48679 48713 48745 48778 48809 48840 48870 48899
3
0,48928
48956 48983 49010 49036 49061 49086 49111 49134 49158
4
0,49180
49202 49224 49245 49266 49286 49305 49324 49343 49361
147
Окончание табл. П1
U
0
1
2
3
4
5
0,49379
49396 49413 49430 49446 49461 49477 49422 49506 49520
6
0,49534
49547 49560 49573 49585 49598 49609 49621 49632 49643
7
0,49653
49664 49674 49683 49693 49702 49711 49720 49728 49736
8
0,49744
49752 49760 49767 49774 49781 49788 49795 49801 49807
9
0,49813
49819 49825 49831 49336 49841 49846 49851 49856 49861
3,0 0,49865
3,5 0,4997674
4,0 0,4999683
4,5 0,4999966
5,0 0,4999997133
148
5
6
7
8
9
СПИСОК ЛИТЕРАТУРЫ
1. Информационные технологии в радиотехнических системах: Учебное
пособие / В.А. Васин, И.Б. Власов, Ю.М. Егоров и др.; Под ред. И.Б.
Федорова. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2003.
2. Перов А.И. Статистическая теория радиотехнических систем: Учебное
пособие / А.И. Перов. – М.: Радиотехника, 2003.
3. Худяков Г.И. Статистическая теория радиотехнических систем :
Учебное пособие / Г.И. Худяков. М.: Издательский центр «Академия»,
2009.
4. Денисенко А.Н. Сигналы. Теоретическая радиотехника : справочное
пособие / А.Н. Денисенко – М.: Горячая линия-Телеком, 2005.
5. Лезин Ю.С. Введение в теорию и технику радиотехнических систем:
Учебное пособие для вузов / Ю.С. Лезин. М.: Радио и связь, 1986.
6. Сборник задач по теории радиосистем / Ю.С. Лезин, В.В. Савченко. –
Горьковский политехнический институт. Горький, 1988.
7. Бакулев П.А. Радиолокационные системы: – учеб. для вузов 2-е изд.
перераб. и доп. / П.А. Бакулев. – М.: Радиотехника, 2007.
8. Радиотехнические системы: Учебное пособие для вузов по
специальности «Радиотехника» / Ю.П. Гришин, В.П. Ипатов, Ю.М.
Казаринов и др.; Под ред. Ю.М. Казаринова. – М.: Высшая школа, 1990.
9. Тихонов В.И. Статистическая радиотехника / В.И. Тихонов. - М.: Сов.
радио, 1982г.
10. Горяинов В.Т., Журавлев А.Г., Тихонов В.И. Статистическая
радиотехника. Примеры и задачи. Учебное пособие для вузов / Под ред.
В.И. Тихонова. - М.: Сов. Радио, 1980г.
11. Математическая статистика: учебник / В.Т. Горяинов, И.В. Павлов, Г.М.
Цветкова, И.О. Тескин, - М.: Изд-во МГТУ, 2001г.
149
СЬЯНОВ ВЛАДИМИР АЛЕКСАНДРОВИЧ
ОСНОВЫ СТАТИСТИЧЕСКОЙ ТЕОРИИ
РАДИОТЕХНИЧЕСКИХ СИСТЕМ
Редактор Е.В. Комарова
Технический редактор Т.П. Новикова
Компьютерная верстка Е.П. Комова
Подписано в печать 15.04.2018 Формат 60х84 1/16 .
Бумага офсетная. Печать офсетная. Усл. печ. л. 8,0.
Тираж 100 экз. Заказ 521
_______________________________________________________________
Нижегородский государственный
Технический университет им. Р.Е. Алексеева.
Типография НГТУ.
Адрес университета и полиграфического предприятия:
603950, г. Нижний Новгород, ул. Минина, 24.
150