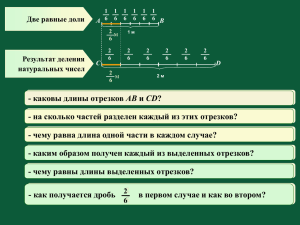
Задание по величинам 1. Описать методику изучения величины длина по методической схеме Величина, так же как и число, является основным понятием курса математики начальных классов, в задачу которого входит формирование у детей представления о величине как о некотором свойстве предметов и явлений, которое прежде всего связано с измерением. В 1-3 классах учащиеся получают представление о таких величинах, как длина, масса, емкость, время, площадь, и о единицах ее измерения. В процессе решения задач они знакомятся с ценой, количеством, стоимостью, скоростью, расстоянием, производительностью и т.д. В процессе изучения темы важно добиться, чтобы учащиеся научились четко дифференцировать такие тесно связанные между собой, но разные по своей сути понятия, как "величина" и "число". Хотя формирование представлений о той или иной конкретной величине и о способах ее измерения имеет свои особенности, тем не менее, целесообразно выделить общие этапы, которые имеют место при изучении каждой из величин: 1. Выяснение и уточнение имеющихся у детей представлений о данной величине (обращение к опыту ребенка). 2. Сравнение однородных величин (визуально, с помощью ощущений, наложением, приложением, путем использования различных мерок). 3. Знакомство с единицей измерения данной величины и с измерительным прибором. 4. Формирование измерительных умений и навыков. 5. Сложение и вычитание однородных величин, выраженных в единицах одного наименования. 6. Знакомство с новыми единицами величины, перевод однородных величин, выраженных в единицах одних наименований, в другие, перевод величин, выраженных в единицах одного наименования, в величины, выраженные в единицах двух наименований, и наоборот. 7. Сложение и вычитание величин, выраженных в единицах двух наименований. 8. Умножение и деление величины на число. С целью формирования представлений о разного рода величинах проводятся практические работы, используются упражнения, применяются демонстрационные и индивидуальные наглядные средства, при этом варьируются коллективные, индивидуальные и групповые формы работы на уроке. Значение с величинами единицами их измерения имеет не только практическое значение: оно предоставляет большие возможности для формирования умения видеть проблему и находить пути ее решения, тем самым способствуя развитию познавательных способностей учащихся. 2. Описать практическую работу по изучению величины длина Знание мер длины, умение находить длину, ширину, высоту и т. п. необходимы учащимся и в быту, и при овладении профессией. Со всеми мерами длины и их соотношениями учащиеся начальной школы знакомятся в течение всего времени обучения в младших классах, закрепление же этих мер проходит в течение всех лет обучения в школе. Знакомство с понятиями длинный - короткий, широкий - узкий, высокий низкий учащиеся получают еще в дошкольный период, коррекция этих понятий осуществляется в дочисловой период. К сожалению, многие дети, приходя из детского сада, считают, что длина, ширина и высота это разные величины. План изучения темы и время введения 1 класс 1. Понятие длины как свойства предметов. Прямая и кривая линии. 2. Отрезок. Сравнение отрезков. 3. Сантиметр. 4. Дециметр. 5. Метр. 2 класс 6. Миллиметр, километр. 3 класс 7. Упорядочивание представлений о длине и единицах ее измерения. Задачи изучения темы 1. Сформировать понятие длины как свойства предметов. 2. Познакомить с единицами длины и соотношениями между ними. 3. Сформировать умения измерять длину данных отрезков и чертить отрезки заданной длины, сравнивать длины. 4. Научить выражать величины в меньших и больших единицах. 5. Научить выполнять действия над величинами устно и в столбик. Предварительно отметим, что измерение длин различными мерками предусмотрено программой детского сада, поэтому многие дети уже знакомы с измерением отрезков различными мерками. Подготовительной работой к введению понятия длины отрезка должны быть упражнения следующего характера. Учитель с первых уроков уточняет отношения длиннее - короче, шире - уже, дальше - ближе. Именно этому помогают упражнения на сравнения предметов по длине (кто выше? что толще? что длиннее?). Важным шагом в формировании понятия длины является знакомство с прямой линией и отрезком как "носителями" линейной протяженности. Сравнивая отрезки "на глаз", дети получают представления о равных и неравных отрезках. При введении (или обобщении) понятия «длина» внимание учащихся необходимо сосредоточить на самом термине «длина», разъяснив соответствующим образом его значение. Так, при проведении беседы можно предложить учащимся сравнить длину карандаша и ручки, которые лежат у них на партах. При сравнении используется прием приложения. Затем можно предложить сравнить по картинке длину ручки и кисточки (ручка короче, кисточка длиннее), сравнить длину красного карандаша и ручки (красный карандаш короче, ручка длиннее). В данной ситуации дети используют сравнение длин предметов «на глаз», т.к. изображения нельзя сравнить ни наложением, ни приложением. Далее представления учащихся уточняются: нарисованные предметы обладают свойством, которое называется длина. Данные предметы можно сравнивать по длине. Отрезки тоже можно сравнивать по длине. На рисунке должно быть хорошо видно, длина какого отрезка больше, а какого меньше. Эти способы сравнения («на глаз», наложением и приложением) можно назвать неопосредованными способами сравнения. При использовании мерок (посредников) мы будем применять опосредованные способы сравнения. Для знакомства с другими способами сравнения длин отрезков рекомендуется организовать практическую работу. Используя полоски из различных материалов, различных цветов, различной длины как модели отрезков, учащиеся сравнивают длины отрезков с помощью различных мерок. Меркой могут выступать узкие полоски бумаги, палочки разной длины и т.д. При использовании различных мерок для измерения одного отрезка учащиеся получают различные числовые результаты. В процессе выполнения различных практических упражнений они должны осознать зависимость числового результата от величины той мерки, с помощью которой измерялся данный отрезок. На уроке это можно легко проверить, рассмотрев следующую ситуацию (предложена Истоминой Н.Б.). На доске начерчен отрезок. Трое детей по очереди измеряют его полосками разной длины. Коля - красной полоской, Миша - зеленой и Дима белой. В результате измерения Коля получил 6, Миша 3, Дима 1. Кто из них оказался прав? Учащиеся заметили, что каждый мальчик был бы прав, если бы указал в ответе единицу измерения: 6 кр., 3 зел., 1 бел. Эту же работу можно провести по индивидуальным карточкам, на которых начерчен один и тот же отрезок. Например, отрезок 4 см. Учитель просит учащихся измерить его. Одни учащиеся измеряют данный отрезок одной клеточкой, другие двумя, а третьи за единицу измерения выбрали 4 клетки. Результат измерения получился разный. На доске делается такая условная запись: После проведения такого рода практических работ у ребят возникает проблема, как же договориться, как измерять длины, чтобы при измерении равных отрезков у всех были одинаковые результаты? Делается вывод, что необходима единая единица длины. Такой единицей измерения является сантиметр. Учитель демонстрирует модель сантиметра в виде узкой бумажной полоски, части спички, кусочка цветной проволоки длиной 1 см. Сантиметр сравнивается с шириной пальца, с длиной двух клеточек тетради. Затем знакомит учащихся с линейкой, с правилами пользования данным инструментом для измерения длин отрезков. На парте у каждого ученика должна быть модель сантиметра, изготовленная учителем заранее. Далее эти задачи решаются при помощи масштабной линейки. Ее могут разметить и сами дети (это интересно). При откладывании отрезков данной длины по линейке на первом этапе ученик должен сначала "прошагать" этот отрезок по сантиметрам, только потом приступать к черчению. Итак, первой единицей измерения отрезков (при изучении чисел от 1 до 10) является 1 см. Учитель предлагает начертить дома еще один отрезок длиной 1 см и изготовить его модель из цветной бумаги или проволоки. При помощи модели ученики должны уметь решить следующие задачи: 1. Измерить заданный отрезок. При этом ученик должен: а) точно приложить конец модели сантиметра к одному из концов отрезка; б) с помощью карандаша на отрезке отметить другой конец модели сантиметра; в) от этого конца продолжить откладывать мерку до тех пор, пока не последняя отметка не совпадет со вторым концом отрезка; г) пересчитав количество вложенных в отрезок моделей, сделать вывод о длине отрезка в см). 2. Начертить отрезок заданной длины. При этом ученик должен: а) провести по линии тетради прямую; б) отметить на ней точку отсчета; в) в нужном направлении откладывать модель, ставя карандашом засечки, отметить второй конец отрезка. Такое пошаговое построение позволяет сформировать у детей необходимые в дальнейшем представления о предупреждении ошибок при дальнейшем измерении. После ознакомления детей с сантиметром, способом измерения длины отрезков сантиметровой линейкой, можно перейти к выполнению упражнений. Задание может быть сформулировано так: Рассмотрите рисунок в задании 3. Каким инструментом можно измерять длину отрезков? Какие правила вы должны выполнять при измерении длины отрезков линейкой? Найдите длину отрезка слева, справа. Затем учитель знакомит учащихся с построением сантиметра в тетради. Конечно, по стандартным клеточкам отрезок длиной 1 см построить не сложно. Рассмотрим последовательность работы. Учитель предлагает детям поставить точку в любом углу клеточки, затем отступить от нее 2 клеточки (вправо, влево, вверх или вниз), поставить вторую точку и соединить их отрезком. Полученный отрезок и будет равен 1 см. Обратите внимание на то, что 1 см ученики должны уметь показать не только от 0 до 1, но и от любого деления: от 4 до 5, от 8 до 9. Кроме того, учащиеся должны видеть не только горизонтальные отрезки и измерять их длину. Положение отрезков обязательно должно варьироваться. Это же относится и к цвету карандаша, которым начерчен отрезок. Также следует учесть и то, что строить отрезки дети должны уметь не только на клетчатой и линованной бумаге, но и на гладкой в различных направлениях. Для закрепления материала с этой целью можно предложить детям практическую работу на индивидуальных карточках: Сначала длины отрезков должны выражаться целым числом сантиметров. Внимание! Основные ошибки, которые допускают учащиеся при построении и измерении отрезков: а) неправильная установка линейки (не с нуля, а с начала линейки); б) начало отсчета с позиции 1, а не ноль; в) наклон головы влево или вправо, что искажает результат (смотреть на линейку необходимо строго вертикально). В процессе овладения навыками измерения отрезков при помощи линейки появляется возможность использовать единичные отрезки как счетный материал для сложения и вычитания, что позволяет проводить пропедевтическую работу к введению числового луча и числовой прямой (направление!), откладывание и изображение чисел при помощи линейки. Следующая единица измерения длины - дециметр вводится при изучении чисел от 11 до 20. Мотивацией является потребность измерять соответствующие длины (длину парты). Моделью сантиметра длину парты измерять долго. Нужна новая единица измерения. Методика аналогична методике ознакомления с сантиметром. Изготавливается модель (картон, дерево). Сначала учитель показывает модель в 1 дм, а затем 1 дм сравнивает с 1 см. Затем вместе с детьми путем прикладывания просчитывается, сколько сантиметров в 1 дециметре. Делается вывод, что 1 дм = 10 см и, наоборот, 10 см = 1 дм. Чтобы учащиеся лучше запомнили протяженность 1 дм, надо, чтобы каждый изготовил из плотной бумаги дециметр, вырезал его, измерил им ленту, бечевку и другие предметы. Учащихся знакомят с обозначением дециметра при числах 1 дм, 2 дм и т.д. Моделью дециметра измеряют отрезки, сначала содержащие лишь целое число дм, а потом - дм и см с использованием уже двух мерок - дм и см. В результате получают составное именованное число. Рассматривается выражение одних именованных чисел через другие. 13 см = … дм … см. Рассуждения проводятся на основе нумерации чисел в пределах 20. 1 дм = 10 см = 1 десяток см. Следовательно, дециметров будет столько же, сколько десятков в числе 13. В числе 13 один десяток и 3 единицы. Значит 13 см = 1 дм 3 см. С единицей измерения длины метром дети знакомятся после изучения дециметра при изучении чисел от 21 до 100. Мотивация к введению новой единицы измерения - потребность измерить длину и ширину класса, коридора и т.д. Попробовав измерять уже знакомыми единицами длины сантиметром и дециметром, дети говорят, что это очень неудобно, получаются большие числа. Учитель просит 3-4 человека измерить длину и ширину класса шагами и результаты измерений, т.е. количество шагов, записать на доске. Сначала дети определяют длину и ширину класса шагами. Они считают количество шагов, уложившихся по ширине или длине класса. Потом можно измерить длину и ширину класса веревкой. Дети растягивают веревку и считают количество шагов от начала до конца веревки и т.д. Когда дети закончат измерять расстояние шагами, запишут результаты на доске, учитель обращает внимание на результаты. Почему они разные? Потому что у всех разные шаги! Нужна новая единица измерения. Потом детям демонстрируется деревянный метр, предметы длиной в 1 м. Проводится практическая работа по измерению длины и ширины класса деревянным метром. Можно продемонстрировать рулетку, складной метр, портняжный "метр". Кроме того, детям можно сказать, что метр можно сделать самим иликупитьв магазине. Метр может быть сделан из дерева (деревянная линейка длиной 1 м), из металла (метр металлический), из клеенки, из бечевки и т.д. Необходимо добиться, чтобы учащиеся не относили длину 1 м только к одному предмету, например к деревянной линейке. Нужно довести до сознания учащихся, что метр - это определенное расстояние, протяженность. Во время изучения темы можно использовать игровой момент. Например, использовать «муравьиные», «лилипутские», «мамины», «папины», «мышкины», обычные и «гигантские» шаги. Можно пронаблюдать с детьми, что чем больше мерка, тем меньше результат и наоборот. Если же всем взять одинаковые шаги и определить ими длину, - то получатся одинаковые числа. Также можно вспомнить мультфильм «Тридцать восемь попугаев», где длина удава измерялась и в «попугаях» и в «мартышках» и в «слонятах». При этом можно выяснить, прав ли был удав, когда сказал: «А в попугаях-то я гораздо длиннее!»? На уроке труда целесообразно организовать работу по закреплению единицы длины метр так, чтобы каждый ученик мог измерить длину и ширину класса. Каждый ученик получает полоску из плотной бумаги длиной 1 м. На полоске написано: 1 м. Дети должны измерять длину и ширину класса по плинтусу, не отклоняясь в сторону (по прямой линии, а не по ломаной, укладывая метровые полоски и делая после каждого метра отметку мелом. Затем они сосчитывают количество метров (1 м, 2 м и т. д.) и записывают результаты измерения на доске. У всех учеников получился один и тот же результат. Таким образом происходит закрепление единицы длины метр. «Что еще можно измерить метрами?» - спрашивает учитель иотмечает,что метр - это мера длины. Далее проводится такая работа: учащиеся сравнивают метр с расстоянием от плеча до кончиков пальцев противоположной вытянутой руки, разводят руки, показывая приблизительно меру длины 1 м, сравнивают свой рост с метром, называют предметы, имеющие длину 1 м, изготовляют метр из плотной бумаги и с его помощью производят измерения. Эталон метра должен находиться в классе. Учащиеся, сравнивая зрительно измеряемый предмет с метром, развивают свой глазомер. Перед измерением того или иного предмета ученик должен определить его размеры на глаз, а потом измерить с помощью линейки. Учащиеся учатся отмеривать («Отмерь 1 м, 3 м, 5 м тесьмы») и измерять отрезки, предметы («Найди длину ленты»). Измерения проводятся в метрах. Учитель также знакомит учеников с записью чисел, полученных при измерениях (1 м, 3 м и т.д.). Уже на этом этапе учащиеся получают первое представление о приближенных измерениях. Если при измерении получается остаток немного больше метра, то он отбрасывается. Если же остаток составляет почти метр, то он принимается за целый метр. Измерения не должны быть самоцелью. Их обязательно нужно связать с какой-либо жизненной ситуацией, с игрой (например, с игрой «Магазин»). В качестве товаров в таком магазине могут быть лента, тесьма, резинка, лоскуты материи, полоски бумаги. На дом целесообразно задать измерить что-либо дома: высоту дверей, холодильника, длину кухни, ширину коридора и т.д. Дети с удовольствием занимаются измерением. На следующих уроках необходимо установить соотношения между м, дм и см. Причем имеет смысл работать по равенствам, как в прямом, так и в обратном прочтении. Таким образом, ознакомившись с единицами измерения длины - сантиметром, дециметром, метром, школьники учатся выражать длину не одной, а несколькими единицами измерения. Вместе с детьми составляется таблица: С самого начала необходимо учить детей определять не только длину, но и ширину, высоту, глубину. При этом важно следить, чтобы ученики при измерении меняли положение линейки, а не измеряемого объекта. С миллиметром и километром дети знакомятся при изучении чисел в 1000 почти одновременно. Мотивация - потребность измерять отрезки, длиной меньшие см и большие расстояния. Наглядное представление о миллиметре дети могут получить, рассматривая линейку с миллиметровыми делениями или миллиметровую бумагу. Сразу же устанавливают соотношения между мм и см. Проводится измерение отрезков в см и мм. Методика изучения темы может быть такой: сначала учитель показывает, что для большей точности измерения необходимо иметь более мелкую единицу измерения длины, чем сантиметр. Для этого он предлагает, например, измерить толщину листа картона. Затем он раздает учащимся карточки, на которых начерчены два отрезка друг под другом, один длиной 4 см, а другой длиной 4 см 5мм, и спрашивает, одинаковые ли отрезки, какой отрезок длиннее, какой короче. Затем учитель предлагает измерить отрезки и спрашивает: «Какова длина верхнего отрезка? Какова длина нижнего отрезка?» При определении длины нижнего отрезка получилось 4 см и остаток меньше 1 см. «Можно ли измерить остаток? - спрашивает учитель. - Какими единицами измерения длины его можно измерить?» Некоторые учащиеся знают единицу измерения длины - миллиметр. Учитель показывает учащимся миллиметр на миллиметровой бумаге, на линейке и просит измерить остаток полоски в миллиметрах. Учащиеся производят также измерение и черчение отрезков в миллиметрах. Слово «миллиметр» записывается на доске и в тетрадях, учитель знакомит с обозначением этого наименования при числах 1 мм, 5 мм и т. д. Необходимо связать изучение новой единицы измерения с уроками труда. Сначала следует попросить учащихся привести самостоятельно примеры, в которых требуется произвести измерение в миллиметрах. Например, если стекольщик вырежет стекло на 2 мм или 3 мм длиннее, то оно не войдет в раму; если сапожник сделает набойку на 3 мм или 5 мм шире каблука, то она будет торчать и испортит вид ботинка, и т.д. Соотношение сантиметра и миллиметра учащиеся устанавливают сами, подсчитывая по линейке, сколько миллиметров содержится в 1 см. Затем на миллиметровой бумаге они отсчитывают 10мм и отмечают отрезок длиной 1 см. Также с помощью миллиметровой бумаги дети производят измерения в миллиметрах сторон геометрических фигур, ученических принадлежностей (карандаша, ручки и т.д.). Результаты измерений учащиеся записывают в виде чисел с употреблением как крупных, так и более мелких единиц измерения. Надо больше предлагать заданий на измерение и построение отрезков, меньших 10мм. Это не только способствует воспитанию навыков точного измерения, но и всегда заставляет помнить о начале отсчета по шкале. При измерении отрезков всех длин нужно давать задания на развитие глазомера: "Определи длину отрезка на глаз. Измерь длину отрезка. Сравни полученные результаты". Далее учащиеся получают знания и о соотношении миллиметра с другими единицами мер длины. Закреплению соотношения мер длины способствуют упражнения на выражение крупных единиц измерения в мелких и, наоборот, мелких единиц измерения в крупных, которые могут сопровождать измерение и вычерчивание отрезков. Например, измерив основание прямоугольника, ученик получил 8 см 5мм. Учитель просит выразить это число в миллиметрах. Километр - единица длины, с которой учащиеся знакомятся после изучения более мелких единиц измерения (1 м, 1 дм, 1 см, 1 мм). Учитель выясняет, какие единицы длины уже знают учащиеся, какие величины можно измерить каждой из известных им единиц, спрашивает, какими единицами измерения длины можно измерить расстояние между городами, селами и т.д. Большинство учащихся правильно называют единицу измерения. Однако почти никто не имеет реального представления об этой единице измерения длины. Представление о километре учащиеся получают лишь тогда, когда они увидят расстояние в 1 км, пройдут этот путь, сами установят связь между расстоянием в 1 км и временем, необходимым, чтобы пройти это расстояние. Все это говорит о том, что понятие о километре нельзя дать учащимся в классе. Урок, на котором учитель знакомит учащихся с новой единицей измерения длины - километром, должен проходить вне школы. Учитель заранее намечает, где ему удобнее познакомить учащихся с километром. Намечает объект, который находится от школы на расстоянии 1 км. Желательно, чтобы, путь проходил по прямой линии. Учитель строит учащихся парами и сообщает, что сейчас они пройдут путь, равный 1 км. Он замечает время, которое потребуется, чтобы пройти этот путь, а также обращает внимание ребят на объекты, мимо которых они проходят. Когда пройден путь в 1 км, учитель снова отмечает время и сообщает: «Мы прошли 1 км, нам понадобилось для этого 15 мин». На обратном пути учитель предлагает посчитать, сколько шагов содержится в 1 км. Первая пара отсчитывает 100 шагов и уходит в конец колонны. Вторая пара также отсчитывает 100 шагов и т.д. Итак, при ознакомлении с километром важно провести практические работы на местности, чтобы сформировать представление об этой единице измерения длины. Для этого можно: отмерять расстояние в 1 км и пройти его вместе с детьми, посчитать, сколько это шагов, провести экскурсию на автовокзал, чтобы узнать расстояние до ближайших населенных пунктов. Этот материал потом удобно будет использовать при составлении задач. Например: «За 15 минут мы прошли 1 км. Сколько км мы пройдем за 1 час, если будем двигаться точно также?» На следующем уроке учащиеся должны (по вопросам учителя) вспомнить, какое расстояние они вчера прошли, сколько времени затратили на путь длиной 1 км. Учитель называет еще ряд объектов, которые находятся на расстоянии 1 км от школы. Затем дети подсчитывают число шагов в 1 км. Дети знают длину своего шага. Длину шага умножают на 1 000. Подсчитывают, сколько метров они прошли. Погрешность в 100-300 м считается допустимой. Учитель отмечает, что если этот путь измерить метрами, то окажется, что в 1 км содержится 1 000 м. Путь в 1 км учащиеся должны проходить неоднократно. На прогулке, экскурсии учитель и воспитатель должны заметить время выхода учащихся из школы, а через 12-15 мин сказать им: «Вы идете уже 15 мин. Какое расстояние за это время вы прошли?» К концу третьего года обучения учащиеся познакомятся со всеми единицами длины, или линейными мерами, и с их соотношениями. Эталоны линейных мер 1 мм, 1 см, 1 дм, 1 м и таблица их соотношений должны постоянно быть в классе. Сводная таблица соотношений между всеми единицами длины. Учащиеся должны уметь применять эту таблицу для выражения найденного результата в различных единицах и для решения практических и учебных задач. Важно! Обратите внимание на то, что в третьем классе выразить длины отрезков с использованием крупных единиц в меньших единицах можно уже двумя способами: 815 cм = ... дм ... см Содержание сводной таблицы учащиеся запоминают, выполняя, например, такие задания: 1) 5 м 7 дм = ... мм. Рассуждения детей могут быть такими: 1 м = 1 000 мм, а 5 м = 5000 мм; 1 дм = 10 см, а 7 дм =70 см; 1 см = 10 мм, 70 см =700 мм; 5000 мм+700 мм= 5700 мм; 2) 3800 мм=... дм. 100 мм= 1 дм. В числе 3800 содержится 38 сотен. Значит, 3800 мм =38 дм; 3) 2005 м = ... км ... м. 1 000 м = 1 км. В числе 2005 содержится 2 тысячи, значит, 2005 м = 2 км 5 м; 4) 8 км 75 м = ... м. 1 км = 1 000 м, 8 км =8 000 м и еще 75 м. Итого получится 8075 м; 5) 5 км 80 м ... 5 км 800 м. 5 км =5 км, 80 м<800 м, поэтому 5 км 80 м <5 км 800 м; 6) 6 м 5 дм ... 6 м 50 см. 6 м =6 м, 5 дм =50 см, поэтому 6 м 5 дм = 6 м 50 см; 7) 4 дм 8 см ... 4 дм 70мм.4 дм = 4 дм, 8 см > 70 мм, значит, 4 дм 8 см > 4 дм 70 мм. Учитель может привести примеры, когда непосредственное измерение длины невозможно, например расстояние между населенными пунктами, кораблями, планетами и др. В таких случаях используются специальные приборы, справочники. Иногда расстояние между пунктами вычисляют по скорости движущегося тела и времени, которое оно затрачивает на прохождение этого расстояния. Итак, понятие «длина отрезка» формируется у детей в процессе математической деятельности: математической организацией эмпирического материала (здесь у детей формируется потребность в измерении длины); логической организации математического измерения); применения математической материала теории (вводится (решаются единица задачи на измерение длин различных отрезков). Таким образом, уже в начальной школе учащиеся получают четкие представления о длине, овладевают умением перевода величин, выраженных в единицах одних наименований, в другие, овладевают измерительными навыками. Полученные знания, умения и навыки закрепляются в тесной связи с изучением нумерации по концентрам. Сложение и вычитание величин, выраженных в единицах двух наименований, рассматривается в концентре "Многозначные числа" при изучении арифметических действий. Усвоение основных признаков понятия величины достигается посредством использования различных практических заданий познавательного характера, представляющих своего рода проблемные ситуации, рассмотрение которых позволяет подвести учащихся к самостоятельным выводам. При работе над темой длина, должна выполняться следующая система упражнений, раскрывающая некоторые свойства понятия длины отрезка, а также подтверждающая справедливость математических законов и для значений величин. I. Упражнения, иллюстрирующие упорядоченность множества отрезков отношением «иметь меньшую длину». 1. Сравните красный и синий отрезки. Какой отрезок короче? Верно ли, что красный отрезок длиннее синего; синий отрезок длиннее красного? (Это упражнение иллюстрирует свойство асимметричности отношения «меньше».) 2. Сравни красный, синий и зеленый отрезки. Назови самый короткий, самый длинный отрезок. Что можно сказать о третьем отрезке относительно самого длинного? Свойство транзитивности отношения «меньше» раскрывается при выполнении следующих заданий. Сравни по длине зеленый и синий отрезки. (Зеленый отрезок короче синего.) Сравни синий и красный отрезки. (Синий отрезок короче красного.) Сравни длины зеленого и красного отрезков. (Зеленый отрезок короче красного. Почему?) Если по длине зеленый отрезок меньше синего, а синий меньше красного, то длина зеленого отрезка меньше длины красного - подводит итог сравнения длин отрезков учитель. II. Упражнения, приводящие к понятию длины отрезка. 1. Определите длину каждого отрезка. 2. Вычислите, на сколько сантиметров длина первого отрезка меньше длины второго отрезка. III. Упражнения, иллюстрирующие переместительное свойство сложения длин отрезков. Расстояние от Москвы до Свердловска 1667 км, а от Свердловска до Новосибирска 1524 км. Чему равно расстояние от Москвы до Новосибирска? Чему равно расстояние от Новосибирска до Москвы? При решении этой задачи составляются такие выражения: 1667+1524 (км) - расстояние от Москвы до Новосибирска; 1524+1667 (км) - расстояние от Новосибирска до Москвы. Решение этой задачи подтверждает свойство переместительности сложения во множестве длин отрезков. IV. Упражнения, иллюстрирующие сочетательное свойство сложения длин отрезков. Расстояние от Москвы до Свердловска 1667 км, от Свердловска до Новосибирска 1524 и от Новосибирска до Иркутска 1851 км. Чему равно расстояние от Москвы до Иркутска? При решении этой задачи следует составить такие математические выражения: (1667+1524) +1851 (км) - расстояние от Москвы до Иркутска; 1667+ (1524 +1851) (км) - расстояние от Москвы до Иркутска. Вычисляя значения этих выражений, учащиеся устанавливают, что сложение величин ассоциативно. V. Задания, иллюстрирующие свойство монотонности сложения в множестве длин отрезков. От села Сосновка до села Красное 24 км, а от села Красное до села Дачное 18 км. Сравнить расстояние от Сосновки до Красного с расстоянием от Сосновки до Дачного. И по чертежу, и по условию задачи учащиеся устанавливают, что 24 < 24 + 18. VI. Задачи, неявно вводящие следующее свойство длины отрезка: длину отрезка можно делить на любое число п одинаковых частей. Начертите отрезок длиной 12 см и разделите его на 3 равные части, а затем каждую из них на 2 равные части. На сколько равных частей можно разделить весь отрезок? Чему равна длина шестой части данного отрезка? Задание по элементам алгебры 1. Составить подробный план-конспект занятия по элементам алгебры в 1 классе с использованием мультимедийных приложений к учебнику Математика Тип урока: урок закрепления знаний. Задачи: - закреплять знания об образовании, обозначении и десятичном составе чисел от 10 до 15; - знание состава чисел в пределах 10; - умение выполнять сложение и вычитание чисел, основанное на знании десятичного состава чисел; - умение решать простые задачи изученных видов; - умение определять время по циферблатным часам с точностью до часа; - развивать вычислительные навыки; - способствовать воспитанию чувства коллективизма. Формы работы: индивидуальная, парная, фронтальная. Оборудование: математика: рабочая тетрадь, мультимедийная презентация, демонстрационный материал, веер цифр, карточки для индивидуальной и парной работы, ларец с письмом. Ход урока 1. Организационный этап - Прозвенел и смолк звонок. Начинается урок. Один, два, три – мир красивый, посмотри, Четыре, пять – солнце светит нам опять, Шесть, семь, восемь – счастье в дом ребенок вносит, Девять, десять – повторим все цифры вместе. Ю.Кирсанова 2. Подготовка учащихся к работе на основном этапе -Сегодня утром у себя на столе я нашла необычный ларец. На нем 6 замков. А рядом записка «Чтобы открыть замки и увидеть, что лежит в ларце нужно выполнить задания. Но выполнить их сможет только тот, у кого есть это качество. (Слайд 2) - Что бы узнать, что помогает справляться с трудностями, нужно выполнить задание. Сначала определите время по часам. (Учитель показывает на циферблате время, какое было, какое стало. Учащиеся показывают с помощью математического веера, который час и определяют, сколько часов прошло.) (Слайды 3,4) (Получилось время: 3 ч - р, 8ч –а, 5 ч – ж, 2 ч –д, 6ч- б, 4 ч- у.) - Если вы расшифруете числа, поставив их в порядке возрастания, то узнаете, что поможет вам выполнять успешно задания, первый замок будет открыт. (Получилось слово «Дружба») (Слайды 5,6) - Какой девиз поможет вам выполнять задания? («Вместе не трудно, вместе не тесно, вместе легко и всегда интересно!») (Слайд 7) - Молодцы, первый замок открыт. - Тема нашего урока: закрепление изученного. Сегодня на уроке мы повторим состав чисел в пределах 10; будем решать примеры с двузначными числами, будем решать задачи. А главное, мы будем делать все дружно и внимательно. 3. Этап актуализации знаний учащихся. Устный счет. 3.1 Задание, которое поможет нам открыть второй замок. (Учитель предлагает рассмотреть ларец). (Слайд 8) - Из каких геометрических фигур состоит ларец? Сколько их? Сколько треугольников? Сколько не треугольников? Какая фигура лишняя? - Второй замок вы открыли. 3.2 Игра «Молчанка» (У учащихся карточки с числами, они вычеркивают ответы). 1) Зачеркни число, состоящее из 1 дес.6 ед. 2) Какое число стоит за числом 19? 3) Какое число стоит перед числом 18? 4) Между числами 14 и 16? 5) К 10 вычесть 1 6) 3 увеличь на 4 7) 6 уменьши на 1 8)Я задумала число, прибавила к нему 2 и получила 12. Какое число я задумала? 9) У Алиночки 12 счётных палочек. Одна сломалась. Сколько же осталось? 10) В коробке 6 карандашей. Маша положила ещё столько же. Сколько карандашей в коробке? 11) Было 10 ананасов, купили еще три ананаса. Сколько ананасов стало? (Слайды 9,10) Учащиеся проверяют по слайду числа, которые остались. Называют их в порядке возрастания: 2, 4, 6, 8. Продолжают закономерность 2, 4, 6, 8, 10, 12. - Третий замок вы открыли. 3.3 Физкультминутка Столько выполним наклонов. Сколько красненьких кругов?(4) Столько выполним прыжков. Сколько звёздочек? Считаем.(5) Столько раз поприседаем. Сколько здесь всего слонов?(3) Столько сделаем шагов. Сколько мышек возле кошки? (4) (Слайды 11,12) 4. Этап закрепления знаний и способов действий 4.1 Задание «Математическое лото» в парах. Учащиеся заполняют листок лото, наложив на него карточки с ответами. Каждая пара получает свой набор карточек лото. 4+6=п ........... 4+6=р 16-10=м ........... 16-10=е 10+3=р ........... 10+3=и 8-3=р ........... 8-3=е 12+0=е ........... 12+0=н 15-1=и ........... 15-1=е 14+1=ы ........... 14+1=ш У пар должны получиться слова «Примеры», «Решение». Выполненное задание пары проверяют по слайду. Оценивают работу пар. (Слайды 13,14) - Ваша дружная работа в парах помогла открыть четвертый замок. 4.2 Работа по учебнику стр. 19. Решение задачи. Сначала автобус ехал 4ч, а потом – 2 ч. Сколько часов ехал автобус? - Прочитайте условие задачи? Прочитайте вопрос задачи? Какое решение будет? Запишите решение в тетради на печатной основе на стр.10. Назовите полный ответ задачи. (Слайды 15,16) - Молодцы, вот и пятый замок смогли открыть. 4.3 Физкультминутка Много вы всего решили. Минуты отдыха наступили. Вы тетрадки отложите И к разминке приступите. (Слайд 17) 5. Этап контроля и самоконтроля знаний и способов действий -Что бы разгадать секрет ларца, нужно выполнить итоговое задание. Оно покажет, как вы умеете выполнять сложение и вычитание с двузначными числами. Заданием выполним в печатной тетради на стр. 10. (Слайд 18) 10+3= ........... 14+ … = 15 14-4= ........... 15-…=14 13+1= ........... 10+…=10 Оцените свою работу. 0 ошибок – высокий уровень 1 ошибка – достаточный уровень 2-3 ошибки - средний уровень (Слайд 19) - Вот и шестой замок вы смогли открыть. 6. Этап подведения итогов и рефлексии - Ларец открывается. В нем находится письмо. Ученики этого класса математику знают: Примеры, задачи решают, Время на часах определяют. Эти ребята дружны и умны, Их ответы всегда верны, Все ошибки побеждены! (Слайд 20) - Оцените свою работу на уроке, используя приём «Зарядка». Поднимите руки вверх и станьте на цыпочки те, кто на уроке не допустил ошибок. Встаньте прямо, руки по швам те, кто допускал на уроке ошибки. Но все ошибки были найдены и исправлены. Спасибо за урок. Задание по арифметическим действиям 1. Составить подробный план-конспект занятия арифметическим действиям в 1 классе с использованием мультимедийных приложений к учебнику Математика 1 Цели урока: Закрепить знание таблицы сложения и вычитания, формировать умение решать задачи; решать задачи с опорой на числовое равенство; учить решать деформированные числовые равенства; учить находить значения числовых выражений; повторить компоненты действия сложения. Развивать логическое мышление, внимание, память, речь, воображение, интерес к математике. Воспитывать умение работать в коллективе, самостоятельность, дисциплинированность, доброжелательность, умение дарить тепло и доброту. УУД: 1. Познавательные: общеучебные – определение состава чисел первых двух десятков; составление и решение задач; выполнение арифметических действий; логические – сравнение чисел и выражений; установление связи между рисунком и арифметическим действием; постановка и решение проблем – самостоятельное создание способов решения проблем учебной задачи. - использование имеющихся знаний; -исследование учебной задач; - установление логических, - построение логической цепи рассуждений; причинно-следственных связей; - применение знаково-символической схемы. 2. Регулятивные: планировать свои действия в соответствии с поставленной задачей и условиями ее реализации; - оценивать уровень успешности; - производить контроль своих действий; -определять цель учебной задачи; - планировать свою деятельность, определяемую результатом, - контроль в форме сличения способа действия и его результата с заданным эталоном. 3. Коммуникативные: - умение слушать и вступать в диалог; - умение правильно выражать свои мысли; - умение контролировать и корректировать действия других; - оформление своей мысли в устной речи; - обоснование своего ответа; - умение ориентироваться в своей системе знаний; 4.Личностные: адекватно судят о причинах своего успеха/неуспеха в учении, связывая успехи с усилиями, трудолюбием, формирование положительного отношения к учению. Фронтальная – составление плана и последовательности действий в ходе решения учебной задачи. Индивидуальная – планирование выполнения заданий самостоятельной работы: образование чисел второго десятка; запись двузначных чисел в пределах 20; выполнение арифметических действий; составление и решение задач; сравнение чисел и выражений; установление связи между рисунком и арифметическим действием; обдумывание ситуации при оценивание своего умения это делать. ЭТАПЫ УРОКА Организационный момент. - 2 мин Сообщение темы и цели урока - 3мин Мозговой штурм.- 10мин Повторение пройденного материала.- 10мин Физ.минутка.- 5 мин Самостоятельная работа. -5 мин Решение задач. - 8мин Итог урока - 2 мин Оборудование: - тетради; - логическое задание; - слова: леший, молодцы, спасибо; - карточки для индивидуальной работы; - алгоритм решения задачи; - ребус; - полоски бумаги для каждого ученика; - снежинки - числа; - презентация, мультимедийная доска; возникновении затруднения и - математический веер; - экран, мультимедийный проектор, компьютер. Ход урока I. Организационный момент. 2 мин Учитель: - Здравствуйте, ребята! Сейчас у нас урок математики. - Ну-ка, проверяй, дружок, Ты готов начать урок? Всё ль на месте, всё ль в порядке? Ручка, книжка и тетрадка? Все ли правильно сидят? Все ль внимательно глядят? -Ребята, сегодня к нам на урок пришли гости. Давайте повернемся к ним, улыбнемся и поприветствуем. ( Доброго дня). И вам ребята, доброго дня и хорошего настроения. Слайд 1 Пусть это утро принесёт нам радость общения, наполнит наши сердца благородными чувствами. Нас приветствует солнышко и дарит нам свои волшебные лучики: добра, счастья, здоровья. Я дарю вам лучик добра. Хочу, чтоб вы были добры друг к другу и добро поможет вам. Давайте повернёмся друг к другу и скажем: Я желаю тебе сегодня добра. Ты желаешь мне сегодня добра. Мы желаем дуг другу сегодня добра. - Ребята, а сейчас закройте глаза. Повторяйте слова за мной: "Я в школе на уроке. Сейчас я начну учиться. Я радуюсь этому. Я готов к этому." Слайд 2 Девиз урока: "Знаешь - говори, не знаешь - молчи!" -Какие качества мы должны взять с собой на урок? ( Сообразительность, смекалку, внимание, память, дружбу, старание и т.д.) II. Сообщение темы и целей урока. 3 мин - Что мы будем делать на уроке математике? - Сегодня на уроке мы повторим то, что учили раньше. Закрепим случаи сложения и вычитания. На уроке нужно быть очень внимательным! Но урок будет не совсем обычным. Я предлагаю вам отправиться в путешествие. Мы отправимся в сказочный лес. Слайд №3 Во время нашего путешествия нам будет светить, и помогать солнышко. Слайд 3 III. Устный счёт. Итак, отправляемся в путешествие. Нас встречает хранительница тайн леса мудрая сова слайд №4. Она приготовила нам задания. Будьте внимательны. Слайд №5 Первое задание. Вот забавная таблица На таблице только геометрические фигуры Повнимательней взгляни. Очень строгому закону подчиняются они У вас у всех на столах есть таблицы Вставьте недостающую фигуру Правильно. Молодцы. С этим заданием вы справились. Ребята, Сова, приготовила ещё задание. Игра "Лабиринт". Слайд №6 Если вы пройдёте через трое ворот и наберёте десять очков, то сможете прочитать имя жителя сказочного леса. Правильно, ребята, это леший. Слайд №8 Слайд №8 Леший - дух леса, враждебный людям. Внешне напоминает человека, только сильно косматого, со спрятанными в гуще волос рожками Ребята, у него не получается решить примеры. Что же делать? Ребята, поможем лешему? Если вы правильно выполняете задание, то появляется буква. Итак, начинаем. Слайд №9 1+4= 2+4= 3+9= 4+4= 7-4= 9-4= 10+6= Слайд № 10 МОЛОДЦЫ! Прочитаем слово, которое получилось МОЛОДЦЫ, значит и с этим заданием вы справились. Двигаемся дальше по нашему волшебному лесу. IV. Повторение пройденного. - Кто же появляется на нашем пути? Отгадайте загадку: Просыпается весной, А зимой под вьюжный вой Спит в избушке снеговой. Кто это? (медведь) Слайд №11 - Что же приготовил нам медведь? И ему нужна помощь? Поможем, ребята? Тогда скорее на помощь медведю. Открываем тетради. Я тетрадочку открою и как надо положу. Я от вас друзья не скрою, ручку я вот так держу. Сяду прямо не согнусь, за работу я возьмусь. - Ребята, какой сегодня день. Какое это число? Что можете сказать про это число? Дети отвечают какое число стоит перед ним, после него. Работа в рабочих тетрадях с. № - Медведь у нас спрашивает: " Что у вас записано?" Дети: - Это числовое выражение. Слайд 12 - А как вы это узнали? Почему так решили? Превратите числовое выражение в числовое равенство. Что для этого нужно сделать? Все дети работают в своих тетрадях, а три ученика на контрольных листочках. (задание трёх уровней сложности) Группа №1 Группа №2 Группа №3 1+9 4+2 4+4 2+7 6-4 7-4 8-3+4 10 - 9-4-1 - Ну, а теперь давайте проверим проверяет первая группа:.. вторая группа: третья группа: 3 + 2 У кого нет ошибок? У кого одна ошибка? Две? Три? Я вижу. Что у вас мало ошибок! Мы помогли мишке, двигаемся дальше. Нарисуйте на полях столбик и зажги на нем свой фонарик. - Идём по лесу, как всё вокруг красиво! Кто это? Слайд №12 - А что это над картинкой? Дети: - Числовое деформированное равенство. Слайд №12 Учитель: - Составьте по равенству и картинке задачу. (На лесной полянке играли 5 зайчат. Прибежали ещё 2. Сколько зайчат стало на полянке?) Слайд 13 - О ком говорится в задаче? Скажите условие задачи. А что ещё есть в задаче? (вопрос) Какой вопрос задачи? Слайд 14,15 - К доске идёт решать задачу:. Записываем и объясняем. Мне известно:.. Надо узнать:. Объясняю решение:. Решаю:. Записываю ответ: Слайд 16,17 - Молодцы! V. Физкультминутка. Ветер тихо клён качает, Вправо, влево наклоняет. (Ноги на ширине плеч, руки за голову. Наклоны туловища вправо, влево) Раз наклон и два наклон, Зашумел листвою клён. (Руки вверх, покружиться) Видишь – бабочка летает, (Взмахи руками) На лугу цветы считает. (Считать пальчиком) Раз, два, три, четыре, пять – (Хлопки в ладоши) Ох, считать, не сосчитает! (Прыжки на месте) Шесть, семь, восемь, девять, десять (Хлопки в ладоши) Даже мудрая пчела (Взмахи руками) Сосчитать бы не смогла! (Считать пальчиком) VI. Повторение изученного раннее. - Идём по лесу дальше, кто нам сейчас встретится? Отгадаем ребус. Слайд №18. Правильно, это лиса. Слайд № 14. У лисички вот какое задание: вам нужно показать знаки сравнений. Слайд №19. Слайд 20 Слайд 21 10 - 4 * 6 9* 8 -1 6+3*8 10 - 3* 8 9* 8 + 1 1 + 7* 8 Молодцы, вы все хорошо справились с заданием лисички! VII. Самостоятельная работа. - А сейчас мы с вами поиграем в игру. Игра называется "Математический спринт". Все жители волшебного леса посмотрят, как вы научились решать примеры. Перед вами лежат полоски бумаги - это "беговые дорожки", так как спринт - это бег на короткие дистанции. Вы должны добежать до финиша, не допустив в примерах ошибок. Итак, я читаю пример, вы записываете только ответ и загибаете листочек, следующий ответ пишите под загнутой частою. (Таким образом, после того, как ученики разогнут листочек, то ответы будут записаны друг под другом.) Итак, начинаем. К двум прибавить семь. Два да шесть, это : Найди сумму чисел четырёх и трёх Десять минус четыре. Первое слагаемое один, второе четыре. Чему равна сумма? Слайд 22 На листочках должен получиться ряд чисел 9,8,7,6,5. - Ребята, это ещё не всё. Волшебный лес просит вас ещё выполнить задание. Из ряда чисел с помощью знаков арифметических действий нужно составить числовых равенства (задание дифференцированного характера): Слайд 23 Группа №1: 2,6,8 Группа №2: 2,3,5 Группа №3: 1,2,3 - Проверяем, как вы выполнили задание, по группам. Молодцы! VIII. Решение задач. Слайд 24 - Но что это? С неба вдруг посыпались снежинки- числа!(Приложение №2) Волшебный лес приготовил вам последнее задание. Отгадайте загадки задачки: 1) У меня четыре книжки, Три машинки и три мишки, Кто ответит побыстрей, Сколько у меня вещей? 10 (С) 2) Цапля по воде шагала Лягушат себе искала. вое прятались в траве, Шестеро под кочкой. Сколько лягушат всего? Только быстро, точно. 8 (П) 3) Дружно муравьи живут. И без дела не снуют. Два несут травинку, Два несут былинку, Три несут иголки, Сколько их под ёлкой? (7) А 4) "У маленькой Светы Четыре конфеты. Ещё три дала Алла. Сколько всего стало"?(7) С 5)"Три ромашки - желтоглазки, Два весёлых василька Подарили маме дети. Сколько же цветов в букете"? (5) И 6)"На кустике перед забором Шесть ярко - красных помидоров. Потом четыре оторвалось, А сколько на кусте осталось"? (2) БО! Называя ответ, ученики по одному выходят к доске и переворачивают снежинку - число. В итоге получается слово СПАСИБО. Слайд 25 IX. Итог урока. - Какое слово у нас получилось? Это говорит вам волшебный лес и все его жители. С вашей помощью жители леса многое поняли и многому научились. V. Рефлексия - Ребята, а чему вы научились на этом уроке? - Какое задание вам показалось самым интересным? - Какое задание вызвало затруднение? -Кто доволен своей работой? - Что лучше всего получалось? - А что было труднее всего? - Ребята, я вам тоже говорю "большое спасибо". Вы все очень хорошо работали. Вам за вашу работу я вам дарю вот такое солнышко. Пусть вам наше солнышко светит всегда. Согревает вас своим теплом. Слайд №1 Урок окончен. До свидание. Задание по нумерации 1. Описать методику изучения нумерации в концентре «100» Изучение нумерации чисел в пределах 100 делится на два этапа: в первом классе изучают числа от 11 до 20, во втором - все числа в пределах 100. Такое деление в концентре "Сотня" обусловленно тем, что многие первоклассники умеют считать числа до 20. Но главная причина в том, что название слов числительных второго десятка отвечает одной закономерности (сначала называется количество единиц, а потом называется десяток - дцать), у записи чисел 11 - 20 прослеживается другая закономерность: сначала пишем цифру, которая помечает один десяток, а потом цифру единиц. Сначала изучается устная нумерация, то есть ученики усваивают название чисел, а потом письменная. Для того, чтобы ученики хорошо усвоили тему, учитель должен широко использовать наглядность: счетные палочки, абаки, нумерационные полоски. На первом этапе формируется понятие о десятке как счетной единице. Начинать можно из такого задания: "Белочка насобирала на зиму полную корзину грибов. (Например - 36 грибов.) Хочет их посчитать, но она может считать только до 10. Долго белочка думала, но смогла все же посчитать все грибы. Кто догадался, как она это сделала"?. На втором этапе учеников знакомят с образованием чисел от 11 до 20 (знакомым им способом: причислением к предыдущему числу единицы, и отчислением от следующего числа единицы), названием чисел. Причем, название чисел можно продемонстрировать на палочках: одну палочку(один) кладем на десять(дцять), проговариваем: один-на-дцять и так далее. Ученики управляются в порядковом и обратном счете чисел в пределах 20, проводят операцию сравнения На третьем этапе переходят к письменной нумерации чисел, обращая внимание на то, что очень важное значение имеет место, на котором мы записываем соответствующие цифры. Эта работа начинается со знакомого уже ученикам числа 10. Вводится понятие однозначные и двузначные числа. На четвертом этапе учеников знакомят с понятиями разрядные единицы, разряд десятков, разряд единиц, а также с образованием чисел из десятка и единиц. Числа от 21 до 100 изучаются во втором классе с начала учебного года. Но этот промежуток числа не отделяется и является продолжением последовательности натуральных чисел 1 - 100. Методические приемы, что использует учитель на этом этапе такие же, как и при изучении чисел первого и второго десятков. Сначала изучается устная нумерация, потом - письменная. В результате изучения нумерации чисел в концентре "Сотня" и проведение соответствующих упражнений, ученики должны хорошо знать названия чисел в данном промежутке, записывать и читать их; осознавать позиционное значение цифры в записи двоцифровых чисел, десятичный состав числа из десятков и единиц; понимать понятие разряд, единицы первого и второго разряда. Новые знания из нумерации чисел в промежутке от 21 до 100 полностью базируются на предыдущих знаниях и умениях учеников. Систематизируя знания учеников о нумерации чисел в пределах 100, учитель предлагает детям предоставлять полную характеристику любому числу. Например, характеризуя число 66 ученики должны: называть общее количество единиц (66 единиц); десятичный состав (в этом числе 6 десятков и 6 единиц; 6 единиц второго разряда и 6 единиц первого разряда); определить место числа в натуральном ряде (число 66 называют во время счета после 65 и перед 67); выделить особенность записи числа ( 66 - число двузначное, для его записи использована дважды цифра 6). Методика изучения сложения и вычитания в пределах 100. Последовательность изучения действий сложения и вычитания обусловлена нарастанием степени трудности при рассмотрении различных случаев: 1. Сложение и вычитание круглых десятков (30+20, 50-20, решение основано на знании нумерации круглых десятков). 2. Сложение и вычитание без перехода через разряд. 3. Сложение двузначного числа с однозначным, когда в сумме получаются круглые десятки. Вычитание из круглых десятков однозначного и двузначного числа 4. Сложение и вычитание с переходом через разряд. Все действия с примерами 1, 2 и 3-й групп выполняются приемами устных вычислений, т. е. вычисления надо начинать с еди­ниц высших разрядов (десятков). Запись примеров производится в строчку. Приемы вычислений основываются на знании учащимися нумерации, десятичного состава чисел, таблиц сложения и вычитания в пределах 10. Действия сложения и вычитания изучаются параллельно. Каж­дый случай сложения сопоставляется с соответствующим случаем вычитания, отмечается их сходство и различие. Такие случаи сложения, как 2+34, 5+45 и др., не рассматри­ваются самостоятельно, а решаются путем перестановки слагае­мых и рассматриваются совместно с соответствующими случаями: 34+2, 45+5. Объяснение каждого нового случая сложения и вычитания про­водится на наглядных пособиях и дидактическом материале, с которым работают все ученики класса. Рассмотрим приемы выполнения действий сложения и вычита­ния в пределах 100: 1) 30+20= 50 Рассуждения проводятся так: 30 — это 3 десятка (3 пучка палочек). 20 — это 2 десятка (2 пучка палочек). К 3 пучкам палочек прибавим 2 пучка, всего получили 5 пучков палочек, или 5 десятков. 5 десятков — это 50. Значит, 30+20=50. Такие же рассуждения проводятся и при вычитании круглых десятков. Подробная запись на первых порах позволяет закрепить последовательность рассуждений. Решение примеров данного вида базируется на уже известных учащимся приемах решения: 54-18=? 18=10+ 8 54-10=44 44- 8=36 Решение этих примеров основывается на разложении второго слагаемого и вычитаемого на разрядные слагаемые и последовательном сложении и вычитании их из первого компонента действия. Чтобы учащиеся приобрели умения и навыки в решении примера сложение и вычитание с переходом через разряд, надо выполнить достаточно много упражнений. Примеры можно давать с двумя, и с тремя компонентами, чередуя действия сложения и вычитания. Решаются и такие примеры: 48+(39— 30). При изучении действий сложения и вычитания в пределах 10 и 20 учащиеся решали примеры с неизвестными компонентами, ис­пользуя прием подбора, например: П+3=10, 4+П=7, П—4=6, 10-П=4. При изучении сотни неизвестный компонент обозначается бук­вой и учащиеся знакомятся с правилом нахождения неизвестных компонентов. Прежде чем познакомить учащихся с решением примеров, со­держащих неизвестный компонент, надо создать ситуацию, приду­мать такую жизненнопрактическую задачу, которая дала бы уча­щимся возможность понять, что по двум известным компонентам и одному неизвестному можно найти этот третий неизвестный компонент. 2. Составить подробный план конспект занятия по теме «Нумерация чисел 20-29», с использованием мультимедийных приложений к учебнику математика Тема: Нумерация чисел в пределах 20-29. Цель урока: способствовать актуализации и закреплению знаний, упражнять в навыках счета. Задачи: 1. Закрепить и обобщить изучаемые приемы сложения и вычитания в пределах 20-29 2. Развивать навык беглого и правильного счета. 3. Решать задачи изученных типов. 4. Развитие интеллектуальных качеств детей. Ход урока: 1. Актуализация знаний. Устный счёт. На доске магнитные карточки с цифрами 21, 23, 24, 26, 27, 29. Дети отвечают с места. - Расположите числа в порядке возрастания. - Расположите числа в порядке убывания. - Какие числа отсутствуют? - Назовите соседей числа 25. - Назовите число, следующее за числом 27. - Назовите число, стоящее между числами 27 и 29. - Назовите число, предшествующее числу 24. - Приготовьте светофоры (двухцветные карточки). Один из учащихся вызывается к доске. Остальные работают с карточками. - Какое число на 24 больше 4? - к заданному числу прибавить 2, то получится 28. Какое число задано? 2. Работа над новой темой. - Назовите все однозначные числа. Почему они так называются? - Приготовьте бусы и отсчитайте 20 бусин. - Прибавьте одну. Сколько получилось? Какой пример можно составить? - Как число 21 можно назвать по другому? (На доске пишу один-надцать) - Добавьте еще одну бусину. Сколько получилось? И т. д.(На доске продолжаю записывать). - Посмотрите на доску. Какая часть в словах остается неизменной? ( надцать) Кто догадался что означают эти на-дцать?( на десяти) - Сколько десятков и единиц в числе 11, 12 и т. д.? - А как же назвать число, в котором 2 десятка? - Переходим к работе в тетради и учебнике. - Откройте тетради и запишите чистописание. 1 2 - Какие двузначные числа можно составить? 4.Закрепление нового материала. Работа по заданию 2 (стр.46 учебника): – Сколько красных флажков на рисунке? Десять. – Как можно сказать по-другому? Десять. Один десяток. – Сколько синих флажков? Как по-другому назвать 10? Один десяток. – Сколько всего флажков на рисунке? 2 десятка. – Два десятка – это сколько единиц? Двадцать. 5. Самостоятельная работа (р.т. с. 23 № 1-4): 1) состав числа в пределах 20 2) установить закономерность в ряде чисел и продолжить 3) найти значения разности (Самостоятельная работа обучающихся. Взаимопроверка) . 6. Физминутка . Карлики- великаны. 7. Закрепление пройденного. Прочитайте текст в задании 3 (с. 47 учебника). Читают текст задачи 3. – Докажите, что это задача. Ответы детей. Прочитайте условие. Прочитайте вопросы задачи. – Какое действие следует выполнить, чтобы ответить на первый вопрос задачи? Сложение. – Почему? Спрашивается, сколько всего деревьев посадили дети. – Запишите решение. – Каким действием будете находить ответ на второй вопрос? Вычитанием. – Почему? Так как спрашивается, на сколько меньше берёзок, чем липок. – Запишите решение. – Ответьте на вопросы задачи. – Как связаны между собой задачи? (Читают тексты задач в задании 4 (с. 47 учебника), выделяют в каждой условие и вопрос, данные и искомое числа, обосновывают выбор арифметического действия, которым будут решать задачи, и самостоятельно записывают решение.) 8. Решение выражений. Задание 7 выполняют устно (с подробным объяснением). Задание под чертой (с. 47 учебника). 9. Проверь себя. Работа в парах. Тестовая работа. Использование электронного приложения к учебнику М.И.Моро по теме «Числа от 1 до 20. Нумерация. Образование, название, сравнение чисел». 10. Итог урока. Рефлексия. -Что нового узнали сегодня на уроке? -Что понравилось? - Что не понравилось? - Что было непонятно?