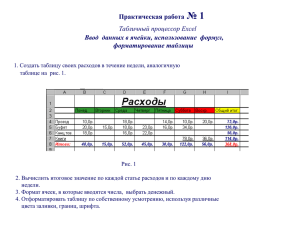
Дифференцирование неявных функций Функция y f (x) может быть задана в неявном виде уравнением F ( x, y ) 0 , не разрешенным относительно y . Например, уравнение x 2 y 2 R 2 или x 2 y 2 R 2 0 задает неявную функцию y от x . Всякую явно заданную функцию y f (x) можно представить в неявном виде уравнением y f ( x) 0 . Но не всякую неявно заданную функцию можно представить в явном виде. Поэтому для нахождения производной функции F ( x; y ) 0 применяют следующие два способа. 1 способ: 1) продифференцировать обе части равенства по переменной x , т.е. x' 1 , а производная от y равна y ' ; 2) полученное уравнение разрешить относительно y ' (выразить y ' ). 2 способ: 1) дифференцируем выражение F ( x, y ) по переменной x , т.е. x' 1 , при этом y рассматриваем как число, т.е. y ' 0 . Это частная производная по x : Fx' x; y . 2) дифференцируем выражение F ( x, y ) по переменной y , т.е. y ' 1 , при этом x рассматриваем как число, т.е. x' 0 . Это частная производная по y : Fy' x; y . 3) находим производную функции y от x по формуле y Fx' x; y (*) Fy' x; y Пример 1. Найти y ' , если x 4 y 3 3xy 0 . Решение: 1 способ: 4 x3 3 y 2 y 3( y xy) 0 4 x3 3 y 2 y 3 y 3xy 0 3 y 2 y 3xy 3 y 4 x3 y(3 y 2 3x) 3 y 4 x3 y 2 способ: по формуле (*): y Fx' x; y 4 x3 3 y 3 y 4 x3 Fy' x; y 3 y 2 3x 3 y 2 3x 3 y 4 x3 . 3 y 2 3x Пример 2. Найти y ' , если ln xy 5 x 2 y 0 . xy' 52 xy x 2 y' 0 y xy' 10 xy 5 x 2 y' 0 xy xy 1 1 y' 1 y 10 x 2 y 1 5 x 2 y ' 10 xy y ' 5 x 2 10 xy y ' . x y x x1 5 x 2 y y 1 10 xy Fx' x; y y 10 x 2 y 1 2 способ: по формуле (*): y ' . x 2 1 Fy x; y x 1 5 x y 2 5x y Решение: 1 способ: Пример 3. Найти y ' , если x 2 y 2 a 2 2 x 2ay Решение: Приведем функцию к виду F ( x, y ) 0 : x 2 y 2 a 2 2 x 2ay 0 . 1 способ: 2 x 2 yy 2 2ay 0 x y y a 1 y 2 способ: по формуле (*): y 1 x ya Fx' x; y 2x 2 1 x . ' Fy x; y 2 y 2a y a