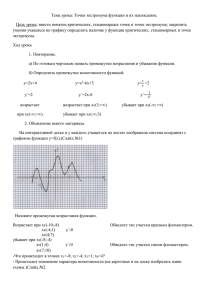
ЗАДАНИЯ B14: ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К

ЗАДАНИЯ B14: ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ
Проверяемые элементы содержания и виды деятельности: владение понятиями монотонность функции, точка экстремума и экстремум функции, производная; знание производных
основных элементарных функций и их свойств; умение находить производные и применять их
к задаче исследования функций на монотонность, экстремумы, наибольшие и наименьшие значения.
Ориентировочное время выполнения учащимися, изучающими математику на базовом уровне: 10—15 минут.
Типы заданий:
Исследование степенных функций.
Исследование произведения показательной функции на многочлен.
Исследование частного двух многочленов.
Исследование функций, содержащих логарифмы.
Исследование тригонометрических функций.
ВНИМАНИЕ: ОСОБЕННОСТИ ЭКЗАМЕНАЦИОННЫХ ЗАДАНИЙ
Задания В14 проверяют знания начал математического анализа, изучаемых в 10—11 классах. Тематика экзаменационных задач традиционна, полностью соответствует школьным учебникам. Предлагаемые задания в целом несложные, решение обычно сводится к реализации несложного алгоритма. При подготовке к экзамену следует повторить таблицу производных и
правила дифференцирования и обратить внимание на различия в понятиях точка экстремума,
экстремум, координаты точки экстремума, наибольшее и наименьшее значение функции.
Производные некоторых элементарных функций.
1)
;
4) (ax)' = ax ln a, a > 0, (ex)' = ex;
2)
5) (sin x)' = cos x;
;
3)
;
6) (cos x)' = - sin x;
Правила дифференцирования.
1. Производная суммы двух функций: 2. Производная произведения двух функций:
3. Производная дроби:
Монотонность и экстремумы функции. Для определения поведения дифференцируемой
на некотором промежутке функции можно использовать следующие утверждения.
Если производная функции положительна на промежутке, то функция возрастает на нем.
Если производная функции отрицательна на промежутке, то функция убывает на нем.
Если производная функции в некоторой точке меняет знак с плюса на минус, то функция
имеет в этой точке максимум.
Если производная функции в некоторой точке меняет знак с минуса на плюс, то функция
имеет в этой точке минимум.
Наибольшее и наименьшее значение функции. Для определения наибольшего и наименьшего значений функции на отрезке используют следующие утверждения.
Пусть функция непрерывна на отрезке. Тогда наибольшее и наименьшее на этом отрезке
значение функции достигается либо в критических точках, либо на концах отрезка.