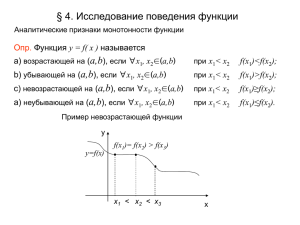
Тема урока: Точки экстремума функции и их нахождение.

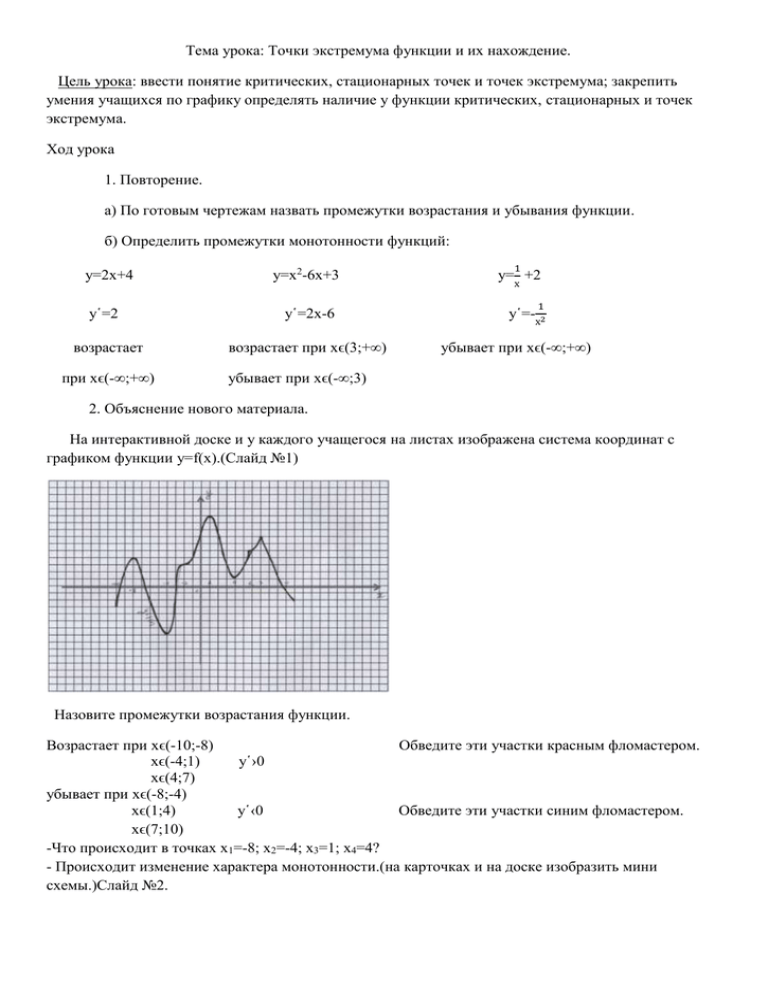
Тема урока: Точки экстремума функции и их нахождение.
Цель урока: ввести понятие критических, стационарных точек и точек экстремума; закрепить
умения учащихся по графику определять наличие у функции критических, стационарных и точек
экстремума.
Ход урока
1. Повторение.
а) По готовым чертежам назвать промежутки возрастания и убывания функции.
б) Определить промежутки монотонности функций:
у=2х+4
у῾=2
возрастает
при хϵ(-∞;+∞)
у=х2-6х+3
у῾=2х-6
возрастает при хϵ(3;+∞)
1
у= х +2
1
у῾=-х2
убывает при хϵ(-∞;+∞)
убывает при хϵ(-∞;3)
2. Объяснение нового материала.
На интерактивной доске и у каждого учащегося на листах изображена система координат с
графиком функции у=f(x).(Слайд №1)
Назовите промежутки возрастания функции.
Возрастает при хϵ(-10;-8)
Обведите эти участки красным фломастером.
хϵ(-4;1)
у῾›0
хϵ(4;7)
убывает при хϵ(-8;-4)
хϵ(1;4)
у῾‹0
Обведите эти участки синим фломастером.
хϵ(7;10)
-Что происходит в точках х1=-8; х2=-4; х3=1; х4=4?
- Происходит изменение характера монотонности.(на карточках и на доске изобразить мини
схемы.)Слайд №2.
- Чему равна производная в этих точках? Касательная к графику функции параллельна оси ОХ (или
даже совпадает с осью ОХ), т.е. производная функции в каждой из указанных точек равна 0.
f(-8) – наибольшее значение функции. но не во всей области определения, а в локальном смысле,
точно также f(-4) наименьшее значение функции, но не во всей области определения, а в локальном
смысле.
При х=7 и х=11 на схемах картина похожа на предыдущие точки, но в этих точках у῾ не существует.
Определение 1. Точку х=х0 называют точкой минимума функции у=f(x), если у этой точки
существует окрестность, для всех точек которой выполняется неравенство f(x)≥f(x0).
Определение 2. Точку х=х0 называют точкой максимума функции у=f(x), если у этой точки
существует окрестность, для всех точек которой выполняется неравенство f(x)≤f(x0).
Значение функции в точке минимума обычно обозначают уmin.
Значение функции в точке максимума обозначают уmax.
Точки максимума и минимума объединяют общим термином – точки экстремума.
Как искать точки экстремума?
В точках -8;-4;1;4 – производная равна 0 –стационарные;
7;11 – не существует – критические.
Теорема. Если функция у=f(x) имеет экстремум в точке х=х0, то в этой точке производная
функции либо равна нулю, либо не существует.
Внутренние точки области определения функции, в которых производная функции равна нулю,
называются стационарными.
Внутренние точки области определения функции, в которых функция непрерывна, но производная
не существует – критическими.
Верна ли обратная теорема: если х=х0 – стационарная или критическая точка, то в этой точке
имеется экстремум.
Посмотрим наш график:
Точка х=-2 – стационарная – экстремума нет;
х=6 – критическая – экстремума нет.
Как же узнать есть ли в стационарной или критической точке экстремум?
Для этого рассмотрим схемы у графика, дописав над осью ОХ у и проанализировав поведение
функции в окрестностях точек.
Наши рассуждения могут служить подтверждением справедливости следующей теоремы.
(учебник стр.185)
Пусть функция у=f(x) непрерывна на промежутке Х и имеет внутри промежутка стационарную или
критическую точку х=х0. Тогда:
а) если у этой точке существует такая окрестность, в которой при х‹х0 выполняется неравенство
f῾(x)‹0, а при x>x0 – неравенство f῾(x)>0, то х=х0 – точка минимума функции у=f(x);
б) если у этой точке существует такая окрестность, в которой при х‹х0 выполняется неравенство
f῾(x)>0, а при x>x0 – неравенство f῾(x)<0, то х=х0 – точка максимума функции у=f(x);
в) если у этой точки существует такая окрестность, что в ней и слева и справа от точки х 0 знаки
производной одинаковы, то в точке х0 экстремума нет.
Вернёмся к нашим схемам.
На практике этой формулировкой пользоваться неудобно, лучше применять условные схемы для
знаков производной.
Рассмотрим на примере, как найти точки экстремума функции.
у=3х4-16х3+24х2-11
1) Найдём производную у῾=12х3-48х2+48х – критических точек нет.
2) Приравняем её к нулю 12х3-48х2+48х=0 12х(х2-4х+4)=0 х1=0, х2=2, 0,2 – стационарные точки.
3) Чертим схему
Рассмотрим алгоритм исследования функции на монотонность и экстремумы. (учебник
стр.187)
3. Закрепление.
Выполнить устно 30.17 – 30.20,
В тетрадях 30.26(а,б)
Д/з : 30.26 (в,г)