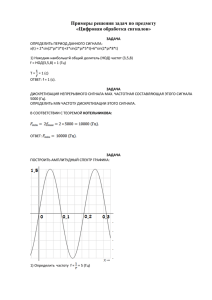
Автор: СЕРГЕЕВА НАТАЛИЯ АРИЕВНА Название образовательной организации: Государственное бюджетное профессиональное образовательное учреждение «Ставропольский колледж связи имени Героя Советского Союза В.А. Петрова» Год и место создания работы: 2016 год, цикловая комиссия естественных и общепрофессиональных дисциплин. Методические указания к выполнению практической работы по дисциплине «Теория электросвязи» «Расчет и построение спектра периодической последовательности прямоугольных импульсов» для студентов 2 курса специальностей: 11.02.11 Сети связи и системы коммутации 11.02.09 Многоканальные телекоммуникационные системы очной формы обучения Цель работы: закрепить знания, полученные на теоретических занятиях, выработать навыки расчета спектра периодической последовательности прямоугольных импульсов. Литература: П.А. Ушаков «Цепи и сигналы электросвязи». М.: Издательский центр «Академия», 2010, с.24-27. 1. Оснащение: 1.Персональный компьютер 2.Описание практической работы 2. Теоретический материал 2.1. Периодический сигнал произвольной формы может быть представлен в виде суммы гармонических колебаний с разными частотами, это называется спектральным разложение сигналом. 2.2. Гармониками называются колебания, частоты которых в целое число раз больше частоты следования импульсов сигнала. 2.3.Мгновенное значение напряжения периодического сигнала производной формы может быть записано следующим образом: 𝑈′(𝑡) = 𝑢0 + 𝑢1 + 𝑢2 + 𝑢3 +. . . . = 𝑢0 + 𝑢𝑚1 𝑠𝑖𝑛(2𝜋𝑓1 𝑡 + 𝜑1 ) + 𝑢𝑚2 𝑠𝑖𝑛(2𝜋𝑓2 𝑡 + 𝜑2 ) + 𝑢𝑚3 𝑠𝑖𝑛(2𝜋𝑓3 𝑡 + 𝜑3 )+. . . . .. Где 𝑢0 −постоянная составляющая, равная среднему значению сигнала за период; 𝑢1 − мгновенное значение синусоидального напряжения первой гармоники; 𝑓1 − частота гармоники, равная частоте следования импульсов; 𝑢𝑚1 − амплитуда первой гармоники; 𝜑1 − начальная фаза колебания первой гармоники; 𝑢2 − мгновенное значение синусоидального напряжения второй гармоники; 𝑓2 = 2𝑓1 − частота второй гармоники; 𝑢𝑚2 − амплитуда второй гармоники; 𝜑2 − начальная фаза колебания второй гармоники; 𝑢3 − мгновенное значение синусоидального напряжения третий гармоники; 𝑓3 = 3𝑓1 − частота третий гармоники; 𝑢𝑚3 − амплитуда третий гармоники; 𝜑3 − начальная фаза колебания третий гармоники; 2.4. Спектр сигнала - это совокупность гармонических составляющих с конкретными значениями частот, амплитуд и начальных фаз, образующих в сумме сигнала. На практике чаще всего используется диаграмма амплитуд Рис. 1 Если сигнал представлен собой периодическую последовательность прямоугольных импульсов, то постоянная составляющая равна 𝑼𝟎 = 𝑼𝒎/𝒔; где Um - амплитуда напряжения ПППИ s - скважность сигнала (S - T/t); T - период следования импульсов; t - длительность импульсов; Амплитуды всех гармоник определяются выражением: Umk = 2Um | sin kπ/s | / kπ где k - номер гармоника; 2.5. Номера гармоника, амплитуды которых равны нулю k = ns где n - любое целое число 1,2,3….. Номер гармоники, амплитуда которой первый раз обращается в нуль, равен скважности ПППИ 2.6. Интервал между любыми соседними спектральными линиями равен частоте первой гармоники или частоте следования импульсов. 𝛥𝑓 = 𝑓 − 𝑓1 2.7 Огибающая амплитудного спектра сигнала ( на рис. 1 показанная пунктирной линией ) выделяет группы спектральных линий называемых лепестками. Согласно рис. 1 каждый лепесток огибающей спектра содержит число линий, равное скважности сигнала. 3. Порядок выполнения работы. 3.1. Получить вариант индивидуального задания , который соответствует номеру в списке журнала группы (см. приложение). 3.2. Ознакомиться с примером расчета (см. раздел 4) 3.3. Рассчитать и построить в масштабе временную и спектральную диаграммы ПППИ, соответствующей вашему варианту. При скважности s<=4 рассчитать 3 лепестка, в противном случае - два. 4. Пример 4.1. Пусть период следования ПППИ Т=.1мкс, длительность импульсов t=0,25 мкс, амплитуда импульса 𝑈𝑚 =10В. 4.2. Расчет и построение временной диаграммы ПППИ. 4.2.1. Для построения временной диаграммы ПППИ необходимо знать период следования импульсов Т, амплитуду и длительность импульсов t, которые известны из условия задачи. 4.2.2. Для построения временной диаграммы ПППИ необходимо выбрать масштабы по осям напряжений и времени. Масштабы должны соответствовать числам 1,2 и 4, умноженным на 10n-(где n=0,1,2,3...). Ось времени должна занимать примерно 3/4 ширины листа и на ней следует разместить 2-3 периода сигнала. Вертикальная ось напряжений должна быть равна 5-10 см. При ширине листа 20 см длинна оси времени должна равна примерно 15 см. На 15-ти см удобно разместить 3 периода , при этом на каждый период будет приходиться L1=5см. Так как период равен 1 мкс, то масштаб по оси времени должен быть равен: Mt=T/Lt=1мкс/5см= 0,2 мкс/см Полученный результат не противоречит выше указанным условиям. На оси напряжений удобно взять масштаб Мu=2В/см (см.рис.2). Рис.2 4.3.Расчет и построение спектральной диаграммы. 4.3.1.Скважность ПППИ равна 𝑇 10−6 𝑆 = = 1∗ =4 𝑡 0.25 ∗ 10−6 4.3.2. Так как скважность S=4, то следует рассчитывать 3лепестка, т.к. 12 гармоник. 4.3.3.Частоты гармонических составляющих равны 𝑓𝑘 = 𝑘𝑓 = 𝑘/𝑇 Где к- номер гармоники, l- период ПППИ. 1 1 𝑓1 = 𝑇 = 1 ∗ 10−6 = 10−6 Гц = 1МГц 𝑓7 = 7𝑓1 = 7 ∗ 1 = 7МГц 𝑓2 = 2𝑓1 = 2 ∗ 1 = 2МГц 𝑓3 = 3𝑓1 = 3 ∗ 1 = 3МГц 𝑓4 = 4𝑓1 = 4 ∗ 1 = 4МГц 𝑓5 = 5𝑓1 = 5 ∗ 1 = 5МГц 𝑓6 = 6𝑓1 = 6 ∗ 1 = 6МГц 𝑓8 = 8𝑓𝑖 = 8 ∗ 1 = 8МГц 𝑓9 = 9𝑓𝑖 = 9 ∗ 1 = 9МГц 𝑓10 = 10𝑓1 = 10 ∗ 1 = 10МГц 𝑓11 = 11𝑓1 = 11 ∗ 1 = 11МГц 𝑓12 = 12𝑓1 = 12 ∗ 1 = 12МГц 4.3.4. Амплитуды составляющих ПППИ равны 𝑈𝑚 10 − 2.5𝐵 𝑈𝑚7 = 2 ∗ 10|𝑠𝑖𝑛7𝜋⁄4|⁄7𝜋 = 0.64𝐵 𝑈𝑚1 = 2 ∗ 10|𝑠𝑖𝑛1𝜋⁄4|⁄1𝜋 = 4.5𝐵 𝑈𝑚2 = 2 ∗ 10|𝑠𝑖𝑛2𝜋⁄4|⁄2𝜋 = 3.2𝐵 𝑈𝑚8 = 2 ∗ 10|𝑠𝑖𝑛8𝜋⁄4|⁄8𝜋 = 0𝐵 𝑈𝑚9 = 2 ∗ 10|𝑠𝑖𝑛9𝜋⁄4|⁄9𝜋 = 0.5𝐵 𝑈𝑚3 = 2 ∗ 10|𝑠𝑖𝑛3𝜋⁄4|⁄3𝜋 = 1.5𝐵 𝑈𝑚10 = 2 ∗ 10|𝑠𝑖𝑛10𝜋⁄4|⁄10𝜋 = 0.64𝐵 𝑈0 = 𝑠 = 4 𝑈𝑚4 = 2 ∗ 10|𝑠𝑖𝑛4𝜋⁄4|⁄4𝜋 = 0𝐵 𝑈𝑚5 = 2 ∗ 10|𝑠𝑖𝑛5𝜋⁄4|⁄5𝜋 = 0.9𝐵 𝑈𝑚6 = 2 ∗ 10|𝑠𝑖𝑛6𝜋⁄4|⁄6𝜋 = 1.06𝐵 𝑈𝑚11 = 2 ∗ 10|𝑠𝑖𝑛11𝜋⁄4|⁄11𝜋 = 0.41𝐵 𝑈𝑚12 = 2 ∗ 10|𝑠𝑖𝑛12𝜋⁄4|⁄12𝜋 = 0𝐵 4.3.5. Математическая модель ПППИ напряжения 𝑢(𝑡) = 2.5 + 4.5 sin(2𝜋106 𝑡 + 𝜑1 ) + 3.2 sin(′𝑙𝜋106 𝑡 + 𝜑2) + 1.5 sin(6𝜋106 𝑡 + 𝜑3) + 0.9 sin(10𝜋106 𝑡 + 𝜑5) + 1.06 sin(12𝜋106 𝑡 + 𝜑6) + 0.64 sin(14𝜋106 𝑡 + 𝜑7) + … 4.3.6.Выбор масштабов. Ось частот располагается горизонтально и при ширине листа 20см должна иметь длину около 15 см. Так как на оси частот нужно показать самую высокую частоту 12 МГц удобно взять масштаб по этой оси Mf=1MГц/см. Ось напряжений располагается вертикально и должна иметь длину 4-5 см. Так как из оси напряжений нужно показать самое большое напряжение 𝑈𝑚1 = 4.5𝐵, удобно взять масштаб по этой оси M=1В/см. 4.3.7.Спектральная диаграмма показана на рис.3 Рис.3 Задание: 𝑈𝑚 = 10𝐵 1. T=0.75мс; τ=0.15мс 2. T=1.5 мкс; τ=0.25мкс 3. T=2.45мс; τ=0.35мс 4. T=13.5мкс; τ=4.5мкс 5. T=0.26мс; τ=0.65мкс 6. Т=0.9мс; τ=150мкс 7. Т=0.165мс; τ=55мкс 8. Т=0.3мс; τ=75мкс 9. Т=42.5мкс; τ=8.5мкс 10. Т=0.665мс; τ=95мкс 𝑈𝑚 = 20𝐵 11. Т=12.5мкс; τ=2.5мкс 12. Т=38мкс; τ=9.5мкс 13. Т=0.9мкс; τ=0.3мкс 14. Т=38.5мкс; τ=5.5мкс 15. Т=0.21мc; τ=35мс 16. Т=2.25мс; τ=0.45мс 17. Т=39мкс; τ=6.5мкс 18. Т=5.95мс; τ=0.85мс 19. Т=48мкс; τ=16мкс 20. Т=1.72мс; τ=0.43мс 𝑈𝑚 = 30𝐵 21.T=24мкс; τ=8мкс 22. T=6.4мс; τ=1.6мс 23. T=7мс; τ=1.4мс 24. T=5.4мс; τ=0.9мс 25. T=17.5мкс; τ=2.5мкс 26. T=1.4мкс; τ=0.35мкс 27. T=5.4мкс; τ=1.8мкс 28. T=2.1мс; τ=0.3мс 29. T=3.5мс; τ=7мс 30. T=27мкс; τ=4.5мкс 𝑈𝑚 = 15𝐵 31. T=4.2мкс; τ=0.7мкс 32.T=28мкс; τ=7мкс 33. T=0.3мс; τ=60мкс