Министерство Образования Российской Федерации Санкт-Петербургский Государственный Университет Кино и Телевидения
реклама

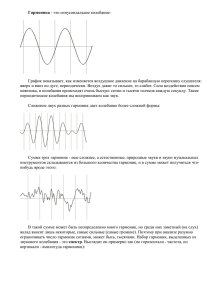
Министерство Образования Российской Федерации Санкт-Петербургский Государственный Университет Кино и Телевидения Факультет экранных искусств Кафедра акустики Контрольная работа по курсу: «Физические основы акустики» выполнил: студент группы ЗР-4 ФЭИ заочного отделения Чернов Александр Викторович Проверил: профессор Вахитов Яшер Шакирович. __________________________________________ Санкт-Петербург 2011 Введение: В данной работе мы знакомимся со сложным периодическим колебанием, которое собственно состоит из простых гармонических колебаний, каждое из которых характеризуется частотой, периодом, амплитудой и начальной фазой. В сложном реальном колебании нет амплитуды и начальной фазы, но есть пиковое значение, и величину отклонения колеблющейся частицы от нулевого значения по оси Y в момент времени t можно найти алгебраической суммой y(t) = y1(t) + y2(t) + y3(t) + ...+ yk(t), где y1(t);y2(t);y3(t);yk(t) - величина отклонения колеблющейся частицы каждого простого колебания, из которых состоит сложное (в момент времени t). Таким образом, можно синтезировать кривую сложного колебания графическим способом. Графический синтез сложного колебания 1.1Задание к 1 3 4 Yk 50 35 20 φ 45 90 0 к — номер гармоники Yk - амплитуда гармоники φ - начальная фаза гармоники 1.2 Описание процедуры графического синтеза Для того чтобы более менее достоверно построить синусоиды 1-й, 3-й и 4-й гармоник надо отмерить 24 см (кратное этим числам). Далее соответственно значениям амплитуд и фаз строим синусоиды каждой гармоники. Теперь по оси времени t через равные промежутки времени отметим точки (шаг дискретизации). Возьмем шаг отсчета равный одной восьмой периода 4-й (самой высокой) гармоники и в каждой точке измерим значения y(t) каждой из функций. Запишем их в таблицу. Затем суммируем эти значения для каждой точки и тоже запишем в таблицу. Из получившихся данных отметим на миллиметровой бумаге точки, соответственно координатным осям Y И t. По этим точкам построим результирующую кривую сложного колебания. 1.3 Таблица 1. K t 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Y1 Y3 Y4 Сумма Y 35 43 48 50 48 43 35 25 12 0 -12 -25 -35 -43 -48 -50 -48 -43 -35 -25 -12 0 12 25 35 35 25 0 -25 -35 -25 0 25 35 25 0 -25 -35 -25 0 25 35 25 0 -25 -35 -25 0 25 35 0 17 17 0 -17 -17 0 17 17 0 -17 -17 0 17 17 0 -17 -17 0 17 17 0 -17 -17 0 70 85 65 25 -4 1 35 67 64 25 -29 -67 -70 -51 -31 -25 -30 -35 -35 -33 -30 -25 -5 33 70 1.4 Заключение: При постоянных амплитудах трех гармоник изменялись значения фаз, такое изменение привело к значительному изменению формы суммарной кривой. Также видно, что если результирующее колебание с фазовыми изменениями гармоник коренным образом меняет форму кривой, то амплитудные изменения влияют только на амплитуду результирующего колебания.