ККР ПРИМЕНЕННИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ ПРИ ПРОВЕДЕНИИ КОНТРОЛЯ КАЧЕСТВА ПРОДУКЦИИ НА ПРЕДПРИЯТИЯХ СТРОЙИНДУСТРИИ

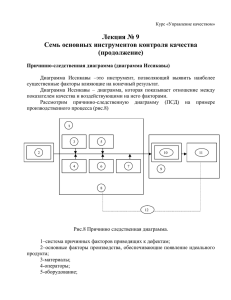
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Тульский государственный университет»
Институт Горного дела и строительства
Кафедра «Строительство, строительные материалы и конструкции»
КОНТРОЛЬНО-КУРСОВАЯ РАБОТА
ПРИМЕНЕННИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ ПРИ
ПРОВЕДЕНИИ КОНТРОЛЯ КАЧЕСТВА ПРОДУКЦИИ НА
ПРЕДПРИЯТИЯХ СТРОЙИНДУСТРИИ
по дисциплине
Основы метрологии, стандартизации, сертификации и контроля качества
Выполнил студент гр.
321061 Пахомов А.А.
Проверил проф. каф. ССМиК
Журавлев Г.М.
Тула - 2018 г.
Введение
Контрольные карты Шухарта используются для статистического
регулирования процессов. Основной задачей статистического регулирования
является
наблюдение за
устойчивостью процесса, предупреждение
нарушений и устранение причин этих нарушений путём соответствующей
регулировки
инструментом,
регулирование
процесса.
с
Контрольная
помощью
процесса.
карта
которого
является
статистическим
осуществляется
Статистический
анализ
контроль
и
осуществляется
посредством выборки и заключается в следующем. Берётся текущая выборка,
состоящая из деталей, изготовленных подряд – одна за другой при
неизменной настройке и других неизменных условиях. Объём выборки и
интервал времени, через который берется выборка,
устанавливается в
зависимости от желаемой точности и стабильности протекания процесса.
Границы регулирования могут быть:
1. статистические границы регулирования Kв и Kн (внутри своего
допуска на изготовления, когда процесс протекает стабильно);
2. заданные заранее предельные значения контролируемого размера Tв
и Tн (технические нормы и допуск на изготовление изделия).
Если последовательность значений точек контроля параметра не
выходит за эти границы, то процесс является статистически управляемым.
При введении контрольных карт следует учитывать:
1.
если
производится
технические
анализ
нормы
процесса
и
на
изготовление
опытным
путём
неизвестны,
то
устанавливается
номинальное значение параметра и допуск, в котором должен протекать
процесс.
2.
если технические нормы на изготовление детали известны,
процесс следует контролировать и управлять им так, чтобы требования
стандарта соблюдались.
Задание к контрольно-курсовой работе
Необходимо осуществить построение и анализ наиболее применяемых
в производстве контрольных карт Шухарта. Для чего по данным выборки №1
построить контрольные карты средних арифметических значений X
и
размахов R (ГОСТ Р 50779.42 – 99). По данным выборки №2 построить
контрольные карты медиан Me и размахов R (ГОСТ Р 50779.42 – 99).
Для построения карт выборку разбить на двадцать подгрупп объемом 5
значений параметра в каждой подгруппе. Провести анализ полученных
контрольных карт и сделать выводы.
Выборка № 1. Производственные данные.
Таблица 1.
№ п/п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
1-я
выборка
130.36
130.37
130.32
130.37
130.41
130.38
130.38
130.36
130.39
130.43
130.31
130.42
130.49
130.50
130.45
130.46
130.38
130.41
130.31
130.41
130.47
130.44
130.28
130.43
130.37
130.39
130.44
130.29
130.38
№ п/п
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
1-я
выборка
130.29
130.32
130.41
130.32
130.37
130.45
130.42
130.41
130.29
130.31
130.36
130.36
130.47
130.34
130.44
130.45
130.35
130.44
130.31
130.36
130.42
130.36
130.25
130.34
130.36
130.44
130.45
130.36
130.39
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
130.29
130.31
130.39
130.37
130.38
130.39
130.41
130.34
130.34
130.41
130.42
130.41
130.36
130.39
130.46
130.43
130.38
130.43
130.42
130.42
130.44
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
130.27
130.32
130.33
130.47
130.44
130.39
130.34
130.35
130.34
130.41
130.34
130.42
130.49
130.46
130.34
130.35
130.33
130.35
130.31
130.53
130.43
Выборка № 2. Производственные данные.
Таблица 2.
№ п/п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
2-я
выборка
150.33
150.33
150.40
150.32
150.40
150.34
150.37
150.37
150.31
150.31
150.32
150.34
150.32
150.34
150.34
150.31
150.37
150.32
150.28
150.31
150.28
150.32
150.37
150.37
№ п/п
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
2-я
выборка
150.39
150.35
150.34
150.35
150.32
150.33
150.31
150.40
150.44
150.40
150.34
150.35
150.31
150.36
150.34
150.37
150.35
150.34
150.29
150.33
150.32
150.35
150.36
150.31
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
150.35
150.33
150.31
150.31
150.35
150.33
150.37
150.42
150.41
150.38
150.30
150.32
150.30
150.31
150.37
150.36
150.32
150.32
150.29
150.32
150.30
150.35
150.33
150.36
150.31
150.35
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
150.36
150.33
150.33
150.31
150.35
150.35
150.31
150.35
150.40
150.34
150.40
150.36
150.27
150.24
150.35
150.36
150.32
150.36
150.35
150.34
150.35
150.33
150.35
150.35
150.37
150.35
1. Построение
контрольных
карт
средних
арифметических
значений X и размахов R.
1.1. Предварительно разобьем выборку на 20 подгрупп объемом по пять
значений параметра в каждой, и вычислим для каждой подгруппы среднее
арифметическое значение и размах по формулам:
n
x
x
i 1
n
где x – среднее арифметическое,
i
,
x – значение в подгруппе, n – количество
i
значений в подгруппе.
R  xmax  xmin ,
(1)
где R – размах значений в подгруппе, xmax и xmin – максимальное и
минимальное значения в подгруппе.
Таблица 3.
№
подгруппы
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
x1
130,36
130,38
130,31
130,46
130,47
130,39
130,31
130,41
130,41
130,38
130,29
130,45
130,36
130,45
130,42
130,44
130,32
130,34
130,42
130,33
x2
130,37
130,38
130,42
130,38
130,44
130,44
130,39
130,34
130,36
130,43
130,32
130,42
130,36
130,35
130,36
130,45
130,33
130,35
130,49
130,35
Значения
x3
130,32
130,36
130,49
130,41
130,28
130,29
130,37
130,34
130,39
130,42
130,41
130,41
130,47
130,44
130,25
130,36
130,47
130,34
130,46
130,31
x4
130,37
130,39
130,5
130,31
130,43
130,38
130,38
130,41
130,46
130,42
130,32
130,29
130,34
130,31
130,34
130,39
130,44
130,41
130,34
130,53
x5
130,41
130,43
130,45
130,41
130,37
130,29
130,39
130,42
130,43
130,44
130,37
130,31
130,44
130,36
130,36
130,27
130,39
130,34
130,35
130,43
Среднее x
130,37
130,39
130,43
130,39
130,40
130,36
130,37
130,38
130,41
130,42
130,34
130,38
130,39
130,38
130,35
130,38
130,39
130,36
130,41
130,39
Размах
R
0,09
0,07
0,19
0,15
0,19
0,15
0,08
0,08
0,10
0,06
0,12
0,16
0,13
0,14
0,17
0,18
0,15
0,07
0,15
0,22
Рассчитаем среднее арифметическое средних и размахов значений для
всех подгрупп:
k
x
x
i 1
k
,
где x – среднее арифметическое средних значений, k – количество подгрупп;
k
R
где
R
R
i 1
i
k
,
– среднее размахов.
Получаем:
x  130.38 ;
R  0.132
1.2. Линии x -карты.
Центральной линией x -карты является линия, проведенная из точки x
по оси ординат, параллельная оси абсцисс:
x  130.38
Верхняя контрольная граница UCL и нижняя контрольная граница
LCL находятся на расстоянии 3
генеральное
стандартное
от центральной линии, где 
отклонение,
используемое
статистикой.
–
По
коэффициенту A2 , взятому из таблицы ГОСТ Р 50779.42-99 в зависимости от
объема выборки рассчитаем контрольные границы:
UCL  x  A2 R  130.38  0.577  0.132  130.46,
LCL  x  A2 R  130.38  0.577  0.132  130.31.
1.3. Линии R-карты.
Центральной линией R-карты является линия, проведенная из точки R
по оси ординат, параллельная оси абсцисс:
R  0.132.
Контрольные границы:
UCL  D4 R  2,114  0.132  0.28,
LCL  D3 R  0  0.058  0.
1.4. Построение контрольных карт.
1.5. Анализ контрольных карт.
На построенных контрольных картах все точки находятся в пределах
контрольных линий, что говорит о статистической управляемости процесса,
т.е. отклонения значений параметра от номинального являются случайными.
2. Построение контрольных карт медиан Me и размахов R.
2.1. Предварительно разобьем выборку на 20 подгрупп объемом по пять
значений параметра в каждой, и вычислим для каждой подгруппы медианы и
размах.
Значение медианы определяется путем ранжирования значений в
подгруппе, например по возрастанию, и для нечетного числа в подгруппе (5),
как среднее число.
Значения в подгруппе: 22.30; 22.18; 22.29; 22.26; 22.26
Ранжированные значения по возрастанию: 22.18; 22.26; 22.26; 22.29;
22.30
Медиана Me=22.26
Значения размахов определяется по формуле (1).
Таблица 4
№
подгруппы
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
x1
150,33
150,34
150,32
150,31
150,28
150,33
150,37
150,32
150,32
150,35
150,39
150,33
150,34
150,37
150,32
150,33
150,31
150,36
150,32
150,33
x2
150,33
150,37
150,34
150,37
150,32
150,31
150,42
150,3
150,32
150,33
150,35
150,31
150,35
150,35
150,35
150,33
150,35
150,27
150,36
150,35
Значения
x3
150,4
150,37
150,32
150,32
150,37
150,31
150,41
150,31
150,29
150,36
150,34
150,4
150,31
150,34
150,36
150,31
150,4
150,24
150,35
150,35
x4
150,32
150,31
150,34
150,28
150,37
150,35
150,38
150,37
150,32
150,31
150,35
150,44
150,36
150,29
150,31
150,35
150,34
150,35
150,34
150,37
x5
150,4
150,31
150,34
150,31
150,35
150,33
150,3
150,36
150,3
150,35
150,32
150,4
150,34
150,33
150,36
150,35
150,4
150,36
150,35
150,35
Медиана
Me
150,33
150,34
150,34
150,31
150,35
150,33
150,38
150,32
150,32
150,35
150,35
150,40
150,34
150,34
150,35
150,33
150,35
150,35
150,35
150,35
Размах
R
0,08
0,06
0,02
0,09
0,09
0,04
0,12
0,07
0,03
0,05
0,07
0,13
0,05
0,08
0,05
0,04
0,09
0,12
0,04
0,04
Рассчитаем среднее значение медиан и размахов значений для всех
подгрупп:
k
Me 
 Me
i
i 1
k
,
k
R
R
i 1
i
k
,
Получаем:
Me  150.344 ;
R  0.07.
2.2. Линии Me -карты.
Центральной линией Me -карты является линия, проведенная из точки
Me по оси ординат, параллельная оси абсцисс:
Me  150.344 .
По коэффициенту A4 , взятому из таблицы ГОСТ Р 50779.42-99 в
зависимости от объема выборки рассчитаем контрольные границы:
UCL  Me  A4 R  150.344  0.69  0.07  150.39,
LCL  Me  A4 R  150.344  0.69  0.07  150.30.
2.3. Линии R-карты.
Центральной линией R-карты является линия, проведенная из точки R
по оси ординат, параллельная оси абсцисс:
R  0.07.
Контрольные границы:
UCL  D4 R  2.114  0.07  0.14,
LCL  D3 R  0  0.07  0.
2.4. Построение контрольных карт.
Анализ контрольных карт.
На построенных контрольных картах все точки находятся в пределах
контрольных линий, что говорит о статистической управляемости процесса,
т.е. отклонения значений параметра от номинального являются случайными.
Список литературы.
1. ГОСТ Р 50779.42-99 «Статистические методы. Контрольные карты
Шухарта».
2. ГОСТ Р 50779.71-99 «Статистические методы. Планы контроля
качества по альтернативному признаку».