Памятка 3 семестр (для вечернего отделения)
реклама

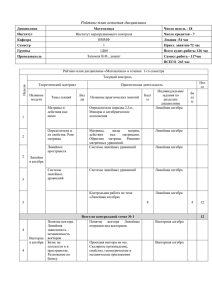
Памятка для студентов групп 5ПГС-61, 5ТГВ-61, 5ИИТ-61, 5Э-61, 5ТМ-61, 5ПИЭ-61 по изучению дисциплины Математика (семестр 3) Составил: ____________ А. В. Фролов ,,___”____________ 2007 года Утверждаю: д.ф.-м.н., профессор, зав. кафедрой ВМ и ММ _________ Г. Н. Леонов ,,___”__________ 2007 г. 1 Содержание дисциплины В 3 семестре будут рассмотрены следующие темы: Тема 8. Дифференциальное исчисление функции нескольких переменных. Понятие функции нескольких переменных. Пределы и непрерывность. Изоповерхности. Дифференцирование функций нескольких переменных. Замена переменных и якобианы. Разложение функции нескольких переменных в ряд Тейлора. Экстремумы, наибольшие и наименьшие значения функции нескольких переменных. Некоторые приложения дифференциального исчисления функций нескольких переменных к геометрии и приближенным вычислениям. Тема 9. Интегральное исчисление функции нескольких переменных. Двойные интегралы и их свойства. Замена переменных в двойных интегралах. Геометрические и механические приложения двойных интегралов. Тройные интегралы и их свойства. Замена переменных в тройных интегралах. Геометрические и механические приложения тройных интегралов. Криволинейные интегралы и их свойства. Приложение криволинейных интегралов к задачам механики и геометрии. Уравнение Пфаффа. Поверхностные интегралы и их свойства. Приложение поверхностных интегралов к задачам физики и геометрии. Внешние дифференциальные формы и их свойства. Формула Грина. Теорема К. Гаусса - М. В. Остроградского. Теорема Стокса. Скалярные и векторные поля, их геометрические и дифференциальные характеристики. Операторы Гамильтона и Лапласа, их выражение в декартовых координатах. Уравнения теплопроводности и непрерывности. Тема 10. Элементы теории функций и функционального анализа. Ряды. Отображения. Норма. Метрические пространства. Линейная зависимость функций и ортогональные базисы. Числовые ряды и их сходимость. Степенные ряды и их сходимость. Разложение функций в ряд Фурье-Эйлера. Теорема Дирихле. Ряды Фурье-Эйлера в комплексной форме. 2 Литература и учебно-методические материалы 1. Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики. – 6-е изд. – М.: Наука, 1986. – 576 с. – 971 экз. 2. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления в 3-х томах. – 2 - е издание – М.: Гостехиздат, 1950. – 150 экз. 3. Шнейдер В. Е., Слуцкий А. М., Шумов А. С. Краткий курс высшей математики. – М.: Высшая школа, 1978. – т. 1 - 383 с. - 82 экз. 4. Сборник задач по математике для втузов под ред. Ефимова А.В., Демидовича Б.П. - М.: Наука, 1986. -т. 1-3. – 462 с., 366 с. Ч.1 – 887 экз.; ч.2 1059 экз.; ч.3 - 313 экз. 5. Рябушко А. П. Сборник индивидуальных заданий по высшей математике. – Минск. “Вышейшая школа” Ч. 1. 1991.- 1140 экз. 3 График контроля Контрольное испытание Время проведения Вес в итоговом рейтинге Примечания ИДЗ 1-4 недели - Зачет / не зачет КР 5 неделя 0,1 5 задач 9 ИДЗ 6-12 неделя 0,3 Оценка 10 ИДЗ 13-17 недели 0,1 Оценка Сессия 0,5 4 задачи и 1 теоретический вопрос Тема 8 Экзамен (по темам 8-10) Примечания: 1. К экзамену допускаются все студенты. 2. «Автоматы» по математике не выставляются. 4 Шкала оценок и правила вычисления рейтинга Соответствие оценок: 75 баллов и выше – «отлично», 50-74 балла – «хорошо», 25-49 баллов – «удовлетворительно», менее 25 баллов – «неудовлетворительно». Рейтинг вычисляется по формуле: RТ R p p i i i Ri – оценка за i-ю контрольную точку, p i – вес этой контрольной точки. , где