ТЕМА урока : Задачи на построение сечений 10 кл
реклама

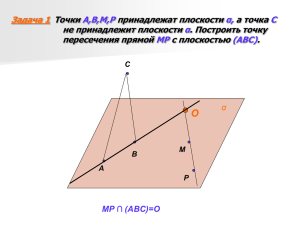
ТЕМА урока : Задачи на построение сечений 10 кл. Цели урока: Создать условия для формирования навыка решения задач на построение сечений; создать условия для развития наглядно-образного мышления, внимания, умения «видеть» в чертеже на плоскости пространственную фигуру; развитие умения планировать свою работу, искать рациональные пути ее выполнения, критически оценивать результат. Тип урока: формирование новых знаний Метод: проблемный, диалогическое изложение, наглядно-иллюстрированный Структура урока I. II. III. IV. V. VI. Организационный момент Актуализация и проверка знаний Формирование новых знаний Формирование новых навыков Подведение итогов Домашнее задание Оборудование: Доска, ПК, презентация «Задачи на построения сечения», карточки «Построить сечения через выделенные объекты». Ход урока I. Организационный момент II. Актуализация и проверка знаний. Задание 1. Дано: А с плоскостью (АВС). (Cлайд 1) Построить точку пересечения прямой МР Задание 2. Дано: Е Задание 3. (Слайд 3) Верно ли утверждение: а) плоскости (АВС) и (А' В' С') параллельны; б) прямые А'В' и СD параллельны; в) прямые А'' В'' и D'С' параллельны; г) точка В' принадлежит плоскости А'СD; д) плоскости (А''В''С'), (А'В'С') и (АВС) пересекаются по одной прямой ; е) плоскости (А''В''С'') и (DСА') пересекаются по прямой, параллельной прямой CD. 2 2.Укажите: а) прямую пересечения плоскостей (А'В'С') и (СDD'); б) прямую пересечения плоскостей (D'OD) и (АВС); в) точку пересечения плоскости АDС и прямой В'В; г) точку пересечения плоскости (ВВ'D') и прямой СD. III. Формирование новых знаний 1. Сообщение темы урока. (слайд 4) 2. Введение понятия секущей плоскости и сечения (слайд 5). D Секущая плоскость Сечение E G F C А B Работа по рисунка:. Учитель раздает карточки, карточки №1,2,3 выполняются вместе с учителем (Слайд 6, 7, 9), карточки №4,5 выполняются самостоятельно, учитель контролирует. Учитель: Сколько плоскостей можно провести через выделенные элементы? Какие аксиомы и теоремы вы применяли? Сделайте вывод, как построить сечение в кубе? В) Дан параллелепипед. Построить его сечение, проходящее через выделенные элементы. Б) Дан параллелепипед. Построить его сечение, проходящее через выделенные элементы. B B A D B A D B C A D C D B C A D B C C A А) Дан параллелепипед. Построить его сечение, проходящее через выделенные элементы. A C D 4. Учащимся предлагается сформулировать правила для построения сечений. Учитель обобщает гипотезы учащихся и делает выводы. (Слайд 10) Для построения сечения достаточно построить точки пересечения секущей плоскости с рёбрами куба (тетраэдра, параллелепипеда). Через полученные точки, лежащие в одной грани, провести отрезки. Многоугольник, ограниченный данными отрезками, и есть построенное сечение. Если секущая плоскость пересекает противоположные грани куба (параллелепипеда) по каким-либо отрезкам, то эти отрезки параллельны. IV. Формирование новых навыков 1. Применяя полученные выводы, построить сечение параллелепипеда плоскостью, проходящей через указанные точки. Задач выполняется двумя способами (Слайд 11,12). B B С С Y D A E X D A E 3 2. Объяснение наиболее сложной задачи на построение сечения параллелепипеда плоскостью, проходящей через три данные точки. (Слайд 13) C B K A D E X Примерные вопросы для фронтальной беседы с классом при показе слайда: Как построить прямую, по которой секущая плоскость пересекает плоскость нижнего основания? По каким прямым секущая плоскость пересекает верхнее и нижнее основания параллелепипеда? Через какую точку проходит прямая, параллельная прямой АЕ? После показа построения ученики выполняют построение в тетрадях. (При необходимости слайд можно показать повторно. Слайд14). Для диагностики достижения целей урока учащимся предлагается задания на готовых чертежах. (Cлайд 15) На каких чертежах изображено сечение прямоугольного параллелепипеда плоскостью α? C B A A D D A D A D D B C B C D A C B A A D B C C B A D B C B C B A B C D A C D C помощью сигнальных карточек, учащиеся должны указать номера правильных ответов: V. Подведение итогов урока. 1. Сегодня на уроке вы окунулись в мир «построения сечений». Давайте вспомним этапы построения сечений многогранника. Какие многоугольники могут при этом получиться в сечении? Теперь вы владеете понятиями: Секущая плоскость Сечение. Умеете: Выполнять задачи на построение некоторых сечений в параллелепипеде. 2. Выставление оценок. VI. Домашнее задание (Слайд 16) 1. §4, п.14 2. Придумать и решить задачу на построение сечения прямоугольного параллелепипеда плоскостью, проходящей через 3 данные точки. Подготовить карточку с данной задачей.