Параллелограмм. Признаки. 1

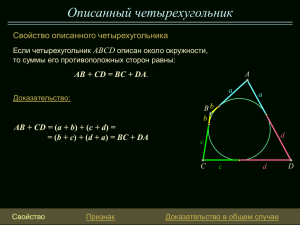
Параллелограмм. Признаки.
1
В
А
О
С
1. Если в четырехугольнике
две стороны равны и
параллельны,
то этот четырехугольник
параллелограмм.
АВ||СD и АВ= СD
D
2. Если в четырехугольнике
противоположные
стороны попарно
равны, то этот
четырехугольник параллелограмм.
АВ=СD, АD= ВС
В
А
О
С
D
3. Если в четырехугольнике
диагонали пересекаются и
точкой пересечения
делятся пополам, то этот
четырехугольник
параллелограмм.
АО=ОС,ВО=ОD
3
Если в задаче нужно доказать,
что четырехугольник является
параллелограммом,
то применяют один из признаков
параллелограмма.или определение
Признаки параллелограмма
1
Если в четырехугольнике две стороны равны и параллельны,
то этот четырехугольник параллелограмм.
В
А
С
D
Дано:
АВСD – четырехугольник,
АВ = CD, АВ ∥ CD
Доказать:
АВСD – параллелограмм
Доказательство
30.11.2012
www.konspekturoka.ru
5
1
В
1 4
А ∆ АBC =
Доказательство
3
С
2
Пусть АВ = СD и АВ ∥ СD,
проведем диагональ АС.
Рассмотрим треугольники
∆ АBC и ∆ACD:
D
∆ACD – по двум сторонам и углу между ними
(АС – общая, АВ = СD – по условию, ∠1 = ∠ 2 как накрест
лежащие при АВ ∥ СD и секущей АС.
Поэтому ∠3 = ∠ 4.
Но ∠3 и ∠ 4 – накрест лежащие углы при пересечении прямых
ВС и AD секущей – АС. Следовательно ВС∥ AD.
Таким образом, если в четырехугольнике противоположные
стороны параллельны, то этот четырехугольник АВСD параллелограмм.
30.11.2012
www.konspekturoka.ru
6
Признаки параллелограмма
2
Если в четырехугольнике противоположные стороны попарно
равны, то этот четырехугольник - параллелограмм.
В
А
С
D
Дано:
АВСD – четырехугольник,
АВ = CD, ВС = АD
Доказать:
АВСD – параллелограмм
Доказательство
30.11.2012
www.konspekturoka.ru
7
2
В
Доказательство
3 2
С
АВСD- четырехугольник,
АВ = CD, ВС = АD.
Проведем диагональ АС.
А
1 4
D
Рассмотрим треугольники
∆ АBC и ∆ACD:
∆ АBC = ∆ACD – по трем сторонам
(АС – общая, АВ = СD, ВС = АD – по условию).
Поэтому ∠1 = ∠ 2 как накрест лежащие при секущей АС.
Отсюда следует, что АВ ∥ СD.
Так как АВ ∥ СD и АВ = СD, то по признаку 1 четырехугольник
АВСD – параллелограмм (если в четырехугольнике две стороны
равны и параллельны, то этот четырехугольник параллелограмм).
30.11.2012
www.konspekturoka.ru
8
3
Если в четырехугольнике диагонали пересекаются и точкой
пересечения делятся пополам, то этот четырехугольник
параллелограмм.
С
В
О
D
Дано:
АВСD – четырехугольник,
ВО = ОD, АО = ОС
Доказать:
АВСD – параллелограмм
А
Доказательство
30.11.2012
www.konspekturoka.ru
9
Доказательство
3
С
В
2
3
О
4
1
D
А
АВСD – четырехугольник,
ВО = ОD, АО = ОС.
Проведем диагонали АС и BD.
Рассмотрим треугольники
∆ АОB и ∆CОD:
∆ АОB = ∆CОD – по первому признаку равенства треугольников
(ВО = ОD, АО = ОС – по условию, ∠ АОB = ∠ CОD – как вертикаль.)
Поэтому АВ = CD и ∠1 = ∠2. Из ∠1 = ∠2 следует, что АВ ∥ CD.
Так как в четырехугольнике АВСD стороны АВ = CD и АВ ∥ CD,
то по 1 признаку четырехугольник АВСD – параллелограмм
(если в четырехугольнике две стороны равны и параллельны, то
этот четырехугольник параллелограмм).
30.11.2012
www.konspekturoka.ru
10
1
Задача
Дано:
Доказать:
В
А
АВСD – четырехугольник,
∠BАC = ∠ACD, ∠CAD =∠BCA
АВСD – параллелограмм.
Доказательство
С
D
Рассмотрим треугольники ∆ АBC
и ∆ACD:
1. ∠BАC = ∠ACD, ∠CAD =∠BCA – по
условию, АС – общая;
следовательно ∆ АBC = ∆ACD – по
стороне и двум прилежащим углам;
поэтому ВС = AD.
2.Так как ∠BАC = ∠ACD – накрест лежащие углы при
параллельных прямых ВС, AD и секущей - АС, то ВС ∥ AD.
3.Так как ВС = AD и ВС ∥ AD, то по 1-му признаку
параллелограмма АВСD – параллелограмм, что и требовалось
30.11.2012
www.konspekturoka.ru
11
доказать.
Как доказать что четырехугольник является
параллелограммом?
1. По определению( стороны попарно
параллельны) 1) АВ|| СD и ВС|| СD
2. две стороны равны и
2) АВ||СD и АВ= СD
параллельны
3. противоположные стороны
попарно равны 3) АВ=СD, АD= ВС
4. диагонали точкой пересечения
4) АО=ОС,ВО=ОD
делятся попалам
В
А
С
О
Д
Задача
Дано:
Доказать:
АВСD – четырехугольник,
BА∥ CD, ∠A = ∠C
АВСD – параллелограмм.
Доказательство
С
В
BА∥ CD – по условию, следовательно
∠1 = ∠ 2 (накрест лежащие)
1 3
А
4
4
2
D
Так как сумма углов треугольника 180°,
то ∠3 = ∠ 4
Рассмотрим треугольники
∆ АBD и ∆BCD:
∆ АBC = ∆ACD – по стороне и двум прилежащим углам
Поэтому BА = CD
(ВD – общая, ∠1 = ∠ 2 , ∠3 = ∠ 4).
Если BА∥ CD и BА = CD, то по 1 признаку параллелограмма
четырехугольник АВСD – параллелограмм, ч. т. д.
03.12.2012
www.konspekturoka.ru
13
Домашнее задание
№ 375
д/м стр 12, С/Р 3, В2
№ 1, 2, 4
30.11.2012
www.konspekturoka.ru
14
№375 (1случай)
В
К
14
7
3
14
1
2
А
Д
С
№375(2 случай)
В
К
7
14
3
7
1
2
А
Д
С