Прыжковая проводимость

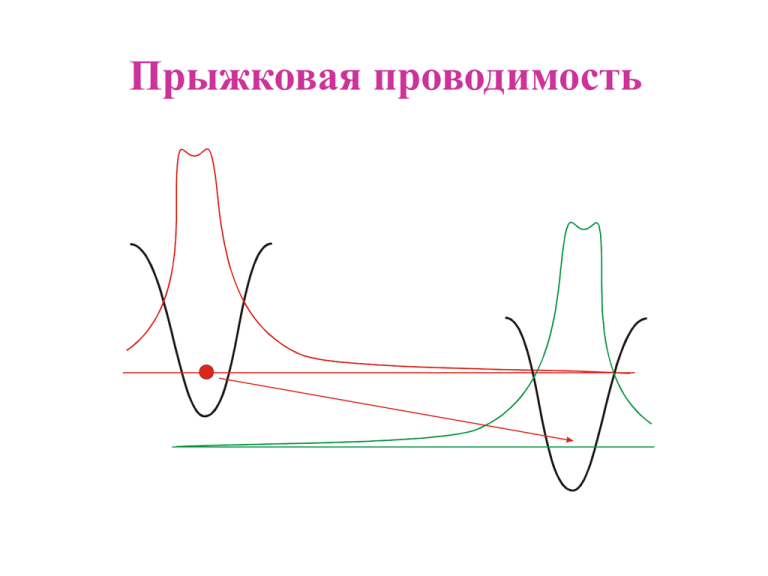
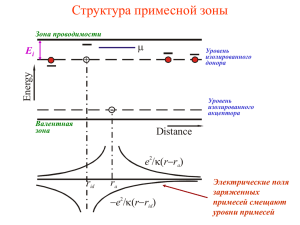
Прыжковая проводимость
Общее определение:
  f (r) e
-r

r
при
Примеры локализованных состояний
I. Центрально-симметричная прямоугольная трехмерная потенциальная яма
U(r) =
0,
r>a
-U0,
r<a
1 - r
 e ,
r


2m | E |
E1
II. Прямоугольная одномерная потенциальная яма
шириной a и глубиной U0
e
-r

,

E2

2m | E |
U
0
III. Притягивающий кулоновский потенциал (атом водорода)
En 
E1
,
2
n
n -1
 n ( r ) r


C
r
exp( - r
n

 2
aB  * 2
me
naB
r
a
0
)
( n  1, 2, 3...)
Вероятность перехода (прыжка)
2
1
2
3
* iqr
3
 F (ij , fi , f j )  | M q | (qs - ij )d q  F (ij , fi , f j )   j e i d r
ij
i - 
f i  (exp
 1) -1
T
ij
ij  (exp
- 1) -1
T
 ij  i -  j
e
-
e
ij
T
-
rij
aB
Сетка Абрахамса- Миллера
i
Rij
j
Rij  R0e
uij
2rij ij
uij 

aB T
Прыжковая проводимость через ближайших соседей
T (K)
300
10 5 4 3
2
10
10
p - Ge
1.5 1.25
0.15
8
10
0.27
0.36
0.49
0.72
0.9
1.4
2.4
3.5
6
(cm)
10
104
102
7.3
1
10-2
0
10
15
53
153
0.2
0.4
0.6
-1
-1
T (K )
g()
-3
NA[10 cm ] = 0.075
16
/D
2
0.8
H.Fritzsche, M.Guevas,
PR 119, 1238 (1960)

1
ij
0
-1
-2
K<<1
Температурно-зависящий
множитель у вероятности всех
прыжков на ближайших соседей
одинаков:
e
-
ij
T
Сравнение с экспериментом
Перколяционный порог
4 3
rc n  Bc  2.7
3
Отсюда
rc  0.865 n
- 13


1
.
73

  0 exp 
1

n 3 aB 

H.Fritzsche, M.Guevas,
PR 119, 1238 (1960)
R. Ray, H.Fan,
PR 121, 768 (1961)
n-GaAs 1.7 1.88 1.9
n-InP
1.9
p-Ge
1.9 1.75 2.0
p-Si
1.8
9
Ge : Ga
(cm)
(cm)
10
6
10
103
100
3
6
9
12
- 1/3
-6
NA (10 cm)
4
10
Si : B
102
100
1.5
-1/3
A
N
2
(10 -6 cm)
Прыжки с переменной длиной; закон Мотта
/D
2
T    D
g()

1
 

 -
ij
0
-1
-2
j
2
i
2
Число состояний в -окрестности N() = g,
-1/3 ,
среднее
K<<1 расстояние мажду ними rij () = [N()]
средняя разность энергий порядка .
Параметр uij (под)сетки Абрахамса-Миллера равен
2

2

uij 
  13 13 
13
aB [ N ()]
T g a B 
T
Величина uij зависит от и достигает минимума, когда
так что
min
 T 

 
13 
 aB g 
3
4
1
 (T TMott ) 4 ,
3
TMott  (aB3 g )-1
d
uij ( )  0,
d
Закон Мотта (продолжение)
Средняя длина прыжка (среднее расстояние r = rij (min) между узлами
1
подсетки) равна
4
-1
r  ( g min )
Сопротивление равно
3
T
 aB  Mott 
T

T
  0 exp  Mott 
T

1
4
(d  3)
Для пленки (d=2) вычисления аналогичны
rij  [ N ( )]
 min
-1
2
2

uij  12
,
1 
2
T
g a B 
,
 T 
  12 
g a 
  B
2
3
1
3
 (T TMott ) , TMott  ( g aB2 ) -1
2
и сопротивление равно
T
  0 exp  Mott 
T

1
3
( d  2)
Прыжки с переменной длиной; закон Шкловского-Эфроса
При наличии кулоновской щели плотность состояний

g ()   2  |  | d -1 , g (0)  0
e 
а количество состояний в -окрестности уровня Ферми
d

 
N ( )   2 
e 
Далее все стандартно
d
rij  [ N ()]
min
-1
d
e2
 ,

 2e T 

 
 aB 
2
uij 
1
2
2
aB [ N ()]
1
 (TTES ) 2 ,
1
d

2e 2

 
 ,
T aB  T
2e 2
TES 
aB
и сопротивление равно
T
  0 exp  ES 
 T
1
2
(d  3, 2)
Прыжки с переменной длиной; эксперимент
Анализ температурных зависимостей (аппроксимация стандартными
функциями)
Очень важно и информативно, но очень опасно
7
10
n-InP
/T (cm/K )
NNH
1/2
6
105
4
10
VRH
1/2
(cm)
10
3
10
102
10
0
2
3
-1
T (K )
-1
8
10
7
10
6
4
1.6
n-InP
8
10
7
10
6
10
105
105
10
4
10
4
10
3
10
3
102
(a)
1
10
/T (cm/K )
8
10
T -1/2 (K -1/2)
0.4 0.8 1.2
10
(b)
0.8
102
10
1.0 1.2 1.4 1.6
T -1/4 (K -1/4)
R. Mansfield, S. Abboudy, F. Foozoni, Philos.Mag. B 57, 777 (1988)
Прыжки с переменной длиной; эксперимент
4 1 0.4
GaAs
10
10
1
N [1016 cm -3]= 0.52
1
-3
8.41
8.30
10
1.1
1.09
2.0
13
8.07
7.90
7.79
7.57
1
Si : As
27
7.39
7.30
6.98
34
1
0.5
0.64
-1
10-2
0
T (K)
18
1
10
4
NA[10 cm ] = 8.48
103
2
100
40 16
-1
(cm)
104
0.04
-1
5
0.1
( cm )
10
T (K)
2
3
-1/2
T (K -1/2)
4
5
R. Rentzsch, K.J. Friedland, A.N. Ionov,
et al.,
phys. stat. solidi b 137, 691 (1986)
0.1
0.4
0.6
T
0.8
1.0
- 1/4
(K )
- 1/4
1.2
W.N. Shafarman, D.W.Koon,
T.G. Castner,
PRB 40, 1216 (1989)
Смена механизмов прыжковой проводимости
Lowering of temperature
Increase in scale
E0
T Thermal delocalization
of carriers

exp (-E0/T)
T Nearest-neighbor hopping
exp [-(-E0)/T)]

E0

 T Variable-range hopping,
Mott law (T>)
exp [-(TM/T) ]
1/4
T


Variable-range hopping,
Efros-Shklovskii law
(T<)
exp [-(TES/T)1/2]
Прыжки с переменной длиной; эксперимент (продолжение)
Проблемы и трудности на примере Si:B
1
10
1
0.25
0.1
1
3
2
10
4
0.1
0.6 0.7 0.8 0.9
-1/4
-1/4
T
(K )
Si:B
n = 0.85 nc
1
10
P. Dai, Y. Zhang, M.P. Sarachik, PRL 69, 1804 (1992)
(cm)
10
3
10
2
1
T
-1/2
2
(K )
-1/2
J.G. Massey, M. Lee,
PRL 75, 4266 (1995)
3
0.2
0.1
0.05
Si :B
n = 0.87 nc
H =0
1
10
0.3
1
10
0.1
0
1
4
0.1
0.6
0.8
T
-1
0
4
1
8
12
1/T (1/K)
T (K)
0.4
-1/4
1.0
(K )
-1/4
16
20
0.1
6
4
2
H =8 T
4
10
24
0.04
(cm)
(cm)
10
4
(cm)
10
T (K )
T (K)
0
102
Si :B
n = 0.87 nc
0
10
1
2
3
T -1/2 (K-1/2)
4
5